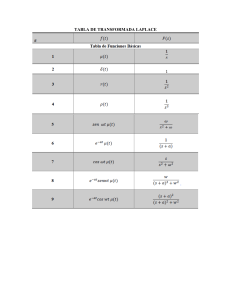
Transformada de Laplace Introducción La transformada de Laplace es una herramienta de gran alcance formulada para solucionar una variedad amplia de problemas del inicial-valor. La estrategia es transformar las ecuaciones diferenciales difíciles en los problemas simples del álgebra donde las soluciones pueden ser obtenidas fácilmente. Entonces se aplica La transformada inversa de Laplace para recuperar las soluciones de los problemas originales. El Método de la transformada de Laplace puede ser operacional ya que se usa para resolver ecuaciones diferenciales lineales. Con el uso de la transformada de Laplace muchas funciones sinusoidales y exponenciales, se pueden convertir en funciones algebraicas de una variable compleja s, y reemplazar operaciones como la diferenciación y la integración, por operaciones algebraicas en el plano complejo. Este método permite usar técnicas gráficas para predecir el funcionamiento de un sistema sin necesidad de resolver el sistema de ecuaciones diferenciales correspondiente Transformada de Laplace y sus aplicaciones La Transformada de Laplace es una herramienta matemática de gran alcance formulada para solucionar una variedad amplia de problemas del inicial-valor. La estrategia es transformar las ecuaciones diferenciales difíciles en los problemas simples del álgebra donde las soluciones pueden ser obtenidas fácilmente. La transformada de Laplace puede ser usada para resolver Ecuaciones Diferenciales Lineales y Ecuaciones Integrales. Aunque se pueden resolver algún tipo de ED con coeficientes variables, en general se aplica a problemas con coeficientes constantes. Un requisito adicional es el conocimiento de las condiciones iniciales a la misma ED. Cuando se resuelven ED usando la técnica de la transformada, se cambia una ecuación diferencial en un problema algebraico. La metodología consiste en aplicar la transformada a la ED y posteriormente usar las propiedades de la transformada. El problema de ahora consiste en encontrar una función en la variable independiente tenga una cierta expresión como transformada. Definición Sea f : [0,+∞) → C una función localmente integrable, esto es, existe la integral de Riemann de f en todo intervalo compacto [0,a] ⊂ [0,+∞). Se define la Transformada de Laplace de f en z ∈ C como +∞ ℒ[𝑓](𝑧) = ∫ 𝑒 −𝑧𝑡 𝑓(𝑡)𝑑𝑡 0 (1.1) siempre que tal integral impropia exista. Como el alumno debe conocer, la convergencia de la integral +∞ ∫ |𝑒 −𝑧𝑡 𝑓(𝑡)|𝑑𝑡 0 implica la convergencia de la integral (1.1). Denotaremos por 𝐷𝑓 el dominio de ℒ[𝑓], es decir, el subconjunto del plano complejo donde la expresión (1.1) tiene sentido. Aplicaciones de la Transformada de Laplace La Transformada de Laplace es una herramienta útil para resolver ecuaciones y sistemas de ecuaciones diferenciales lineales con coeficientes constantes. Como comentamos en la introducción del tema, estas ecuaciones aparecen de forma natural. Para ilustrar el método, consideremos el siguiente ejemplo: la ecuación 𝑦 ′′ + 𝑦 = cos 𝑡 (2.1) junto con las condiciones iniciales 𝑦(0) = 0; 𝑦 ′ (0) = 1 (2.2) Básicamente se trata de aplicar la Transformada de Laplace y sus propiedades a (2.1) de manera que teniendo en cuenta (2.2), nuestro problema se convierte en el problema algebraico 𝑧 2 ℒ[𝑦](𝑧) − 𝑧𝑦(0) − 𝑦 ′ (0) + ℒ[𝑦](𝑧) = 𝑧2 𝑧 +1 de donde ℒ[𝑦](𝑧) = 𝑧2 + 𝑧 + 1 (𝑧 2 + 1)2 Una vez obtenida ℒ[𝑦], hemos de usar la Transformada inversa para volver atrás y recuperar la solución del problema y. En este caso, ℒ[𝑦] satisface las condiciones del teorema, por lo que 𝑦(𝑡) = 𝑅𝑒𝑠 (𝑒 𝑡𝑧 𝑧2 + 𝑧 + 1 (𝑧2 + 1)2 , 𝑖) + 𝑅𝑒𝑠 (𝑒 𝑡𝑧 𝑧2 + 𝑧 + 1 (𝑧2 + 1)2 , −𝑖) = (1 + 𝑡/2) sin 𝑡. una vez realizados los cálculos. Conclusión Como pudimos observar el método de la transformada de Laplace no es más que un método operacional que puede usarse para resolver ecuaciones diferenciales lineales, ya que su uso hace posible que diversas funciones sinusoidales, sinusoidales amortiguadas y exponenciales, se puedan convertir en funciones algebraicas de una variable compleja s, y reemplazar operaciones como la diferenciación y la integración, por operaciones algebraicas en de funciones compleja equivalentes. Por lo tanto, una ecuación diferencial lineal se puede transformar en una ecuación algebraica de la variable compleja s. Es característico del método de la Transformada de Laplace, el uso de técnicas gráficas para predecir o analizar el funcionamiento de un sistema sin tener que resolver las ecuaciones diferenciales. Otra ventaja es que con este método se resuelve la ecuación diferencial obteniendo, simultáneamente, las componentes del estado transitorio y estacionario de la solución.