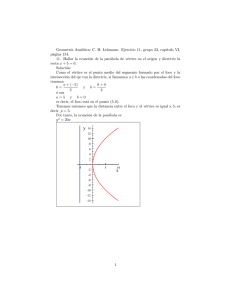
MATEMATICAS V 1500 1. Hallar la ecuación de la

GUIAS DE ESTUDIO DEL QUINTO PERIODO CICLO ESCOLAR 2013-2014 QUINTO GRADO
Estas guías tienen como objetivo ser un reforzamiento para la preparación de los exámenes del período; no
contienen el 100% de los temas que se abarcan en éstos, el alumno debe resolverlas en casa, consultando
dudas con su maestro y debe basarse para su estudio en el trabajo en clase realizado en su libreta y libro.
MATEMATICAS V 1500
1. Hallar la ecuación de la circunferencia con centro en el origen y radio r
a. Hallar la ecuación de la circunferencia de radio 3 y centro (3,4)
b. Hallar la ecuación de la circunferencia de radio 2/3 y centro (-2,4)
c. Hallar la ecuación de la circunferencia de radio 2 y centro (0,2)
2. Determinar el centro y radio de la circunferencia ax 2 +by2 = c
3x2+3y2 = 432
2x2+2y2 = 50
5x2+5y2 = 20
3. Dada la ecuación general de la circunferencia Determina el radio y centro
x2+y2 -6x +12y -23 = 0
x2+y2 +8x +18y -12 = 0
2x2+2y2 -12x +36y +12 = 0
4. Determine la ecuación de la Parábola con vértice en el origen, y foco , lado recto o directriz
a. Hallar la ecuación de la parábola con vértice en el origen y foco (0,6)
b. Hallar la ecuación de la parábola con vértice en el origen y directriz x = -3
c. Hallar la ecuación de la parábola con vértice en el origen y foco (0,-6)
5. Determina las coordenadas del vértice , foco, lado recto y directriz de la parábola con vértice em el
origen
a) y2 =20x
b) x2 = 10
c) x2 =14y
GU5P5
1/3
GUIAS DE ESTUDIO DEL QUINTO PERIODO CICLO ESCOLAR 2013-2014 QUINTO GRADO
Estas guías tienen como objetivo ser un reforzamiento para la preparación de los exámenes del período; no
contienen el 100% de los temas que se abarcan en éstos, el alumno debe resolverlas en casa, consultando
dudas con su maestro y debe basarse para su estudio en el trabajo en clase realizado en su libreta y libro.
6. Dados los parámetros foco, vértice, lado recto o directriz Hallar la ecuación general de la parábola
a) Vértice V (2, 4); Foco F (2, 0)
b) Vértice V (0, 0); Directriz x +2 =0
c) Directriz y –1 =0; Foco (0, -3)
7. Problemas de aplicación de la parábola
1. El cable de suspensión de un puente colgante adquiere la forma de un arco de parábola.
Los pilares que lo soportan tienen una altura de 60 m. y están separados por una distancia de 500 m.,
quedando el punto más bajo del cable a una altura de 10 m. sobre la calzada del puente. Tomando como
eje y el eje de simetría de la parábola, encuentra:
a) La ecuación de la parábola.
b) La altura de un punto situado a 80 m del centro del puente.
2. La función de demanda de cierto producto es: 3p + q2 + 5q –102 = 0 y la ecuación de su oferta e : p 2q2 + 3q + 71 = 0 donde p es el precio y q es la cantidad.
a) Construye las gráficas de oferta y demanda
b) Determina los puntos de equilibrio (son los puntos de intersección, oferta y demanda)
c) Haz el análisis de la zona de beneficio y de pérdida.
3 Un reflector está diseñado de tal manera que la sección transversal que pasa por su eje es una parábola
con su foco en la fuente de luz. Si el reflector mide 3 pies de ancho en la abertura y un pie de profundidad,
encuentra el foco.
8. Hallar la ecuación de la elipse con centro en el origen dados los parámetros
a) C (0, 0); eje menor sobre el eje y; a =4; b =3
b) C (0, 0); eje mayor sobre el eje x; a =5; b =2
c) C (0, 0); F (2, 0); e =1/3
9. Hallar los parámetros dada la ecuación con centro en el origen
a) y2 /25 + x2 /16 =1
b) y2 /169 + x2 /144 =1
c) y2 /25 + x2 /4 =1
GU5P5
2/3
GUIAS DE ESTUDIO DEL QUINTO PERIODO CICLO ESCOLAR 2013-2014 QUINTO GRADO
Estas guías tienen como objetivo ser un reforzamiento para la preparación de los exámenes del período; no
contienen el 100% de los temas que se abarcan en éstos, el alumno debe resolverlas en casa, consultando
dudas con su maestro y debe basarse para su estudio en el trabajo en clase realizado en su libreta y libro.
10. Dada la ecuación de la elipse con centro em (h,k) hallar los parámetros
g) 9 x2 +8 y2 +54x –16y –199 =0
h) 3 x2 + 8 y2+6x –12y –62 =0
i) 4x2 + y2 –8x +4y +4 =0
11. Hallar la ecuación de la Hipérbola con centro en el origen dados los parámetros
A)
C (4, 0); F’ (4, -16); el eje conjugado mide 10
(eje conjugado = 2b)
b) C (-3, 5); F’ (5, 5); el eje transverso mide 10. (Eje transverso = 2a)
c) C (0, 0); F (13, 0); una asíntota es y =5/12x
12. Hallar los parámetros dada la ecuación de la hipérbola con centro en el origen
a) x2 /16 - y2 /4 =1
b) y2 /16 - x2 /4 =1
c) y2 /25 - x2/9 =1
13. Dada la ecuación de la hipérbola con centro em (h,k) hallar los parámetros
a) 9 x2 –16 y2 –54x +64y –127 =0
b) 3 x2 –2 y2 +4y –26 =0
c) 9 x2 –4 y2 +90x +189 =0
14. Representación ¿Qué cónica representa cada ecuación?
a)2x2-5y2 -6x +8y -12 = 0
b) x2+y2 -6x +8y -12 = 0
c) 2x2+4y2 -6x +8y -12 = 0
d) 2x2--6x +8y -12 = 0
GU5P5
3/3