PROBLEMAS DE CINÉTICA QUÍMICA RESUELTOS. 1. Una
Anuncio
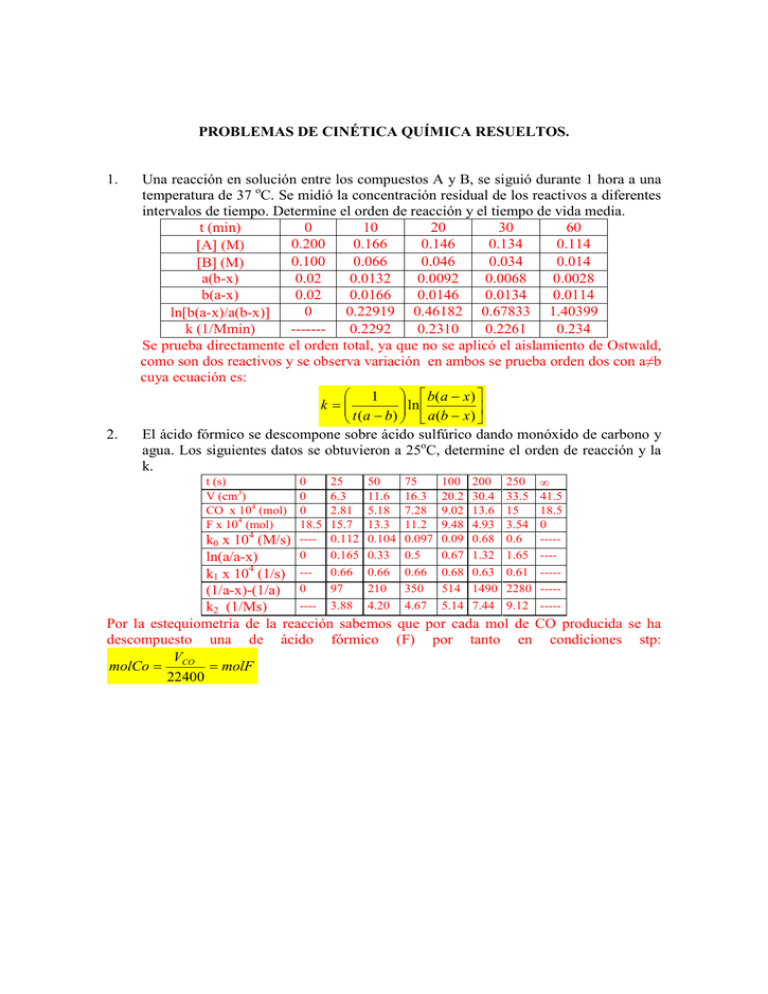
PROBLEMAS DE CINÉTICA QUÍMICA RESUELTOS. 1. 2. Una reacción en solución entre los compuestos A y B, se siguió durante 1 hora a una temperatura de 37 oC. Se midió la concentración residual de los reactivos a diferentes intervalos de tiempo. Determine el orden de reacción y el tiempo de vida media. t (min) 0 10 20 30 60 0.200 0.166 0.146 0.134 0.114 [A] (M) 0.100 0.066 0.046 0.034 0.014 [B] (M) a(b-x) 0.02 0.0132 0.0092 0.0068 0.0028 b(a-x) 0.02 0.0166 0.0146 0.0134 0.0114 0 0.22919 0.46182 0.67833 1.40399 ln[b(a-x)/a(b-x)] k (1/Mmin) ------0.2292 0.2310 0.2261 0.234 Se prueba directamente el orden total, ya que no se aplicó el aislamiento de Ostwald, como son dos reactivos y se observa variación en ambos se prueba orden dos con a≠b cuya ecuación es: 1 b( a − x ) ln k = t (a − b) a (b − x) El ácido fórmico se descompone sobre ácido sulfúrico dando monóxido de carbono y agua. Los siguientes datos se obtuvieron a 25oC, determine el orden de reacción y la k. t (s) V (cm3) CO x 104 (mol) F x 104 (mol) 0 0 0 18.5 ---0 --0 ---- 25 6.3 2.81 15.7 0.112 0.165 0.66 97 3.88 50 11.6 5.18 13.3 0.104 0.33 0.66 210 4.20 75 16.3 7.28 11.2 0.097 0.5 0.66 350 4.67 100 20.2 9.02 9.48 0.09 0.67 0.68 514 5.14 200 30.4 13.6 4.93 0.68 1.32 0.63 1490 7.44 250 33.5 15 3.54 0.6 1.65 0.61 2280 9.12 ∞ 41.5 18.5 0 -------------------- k0 x 104 (M/s) ln(a/a-x) k1 x 104 (1/s) (1/a-x)-(1/a) k2 (1/Ms) Por la estequiometría de la reacción sabemos que por cada mol de CO producida se ha descompuesto una de ácido fórmico (F) por tanto en condiciones stp: V molCo = CO = molF 22400 0.0020 0.0018 n=0 (a-x) (moles formico) 0.0016 0.0014 0.0012 0.0010 0.0008 0.0006 0.0004 A 0,00167 7,49207E-5 B -5,85422E-6 5,58911E-7 -----------------------------------------------------------R SD N P ------------------------------------------------------------0,97373 1,29201E-4 8 <0.0001 ------------------------------------------------------------ 0.0002 0 50 100 150 200 250 t (s) 1.8 n=1 1.6 1.4 -3 1.2 -1 K1= 6.61 x 10 (s ) 1.0 ln(a/a-x) 0.8 0.6 -----------------------------------------------------------A 0,00124 0,00188 B 0,00661 1,40332E-5 ------------------------------------------------------------ 0.4 0.2 R SD N P -----------------------------------------------------------0,99999 0,00324 8 <0.0001 ------------------------------------------------------------ 0.0 -0.2 0 50 100 150 t (s) 200 250 2500 n=2 2000 1500 (1/a-x) - (1/a) 1000 A -209,43319 108,497 B 8,86565 0,80939 ------------------------------------------------------------ 500 R SD N P -----------------------------------------------------------0,9759 187,10349 8 <0.0001 ------------------------------------------------------------ 0 0 50 100 150 200 250 t (s) Se aisló una cepa de S. aureus de un producto lácteo contaminado, se resembró en un medio de Baird Parker e incubó a 35oC durante 48 hrs., después de este tiempo se contaron 500 colonias, en ese momento se le agregó un antibiótico efectivo contra este microorganismo y se observó una disminución en el número de colonias. En las 24 hrs. posteriores a la adición de antibiótico la muerte microbiana presentó una constante de rapidez de 0.0077 hrs-1. Después de este tiempo se observó un cambio en el comportamiento cinético del fenómeno y para el mismo cultivo se determinó una constante de rapidez de 25 colonias/hr hasta la total eliminación de los microorganismos. Calcule el tiempo en que se eliminaron todos los microorganismos de este cultivo. Primeras 24 horas: k= 0.0077 hrs-1 por tanto es orden uno de modo que el número de colonias después de ese tiempo es: (a-x) = 415.64 colonias ln(a − x) = ln a − kt = ln 500 − 0.0077 * 24 = 6.0298 Las siguientes horas hasta la muerte de todas las colonias, k = 25 Colonias/hr. Por tanto es orden cero, de manera que el tiempo para que mueran las 415.64 colonias que había cuando el régimen de orden cero inició es: a − (a − x) 415.64 − 0 = t= = 16.63hr k 25 Ahora el tiempo para la muerte de las 500 colonias es t= 24 + 16.63 = 40.63 hr 4. Si se ponen 100 bacterias en un matraz de 1 L, con el medio de cultivo apropiado, a una temperatura de 40oC, encontrará: a) Prediga el número de bacterias que habrá a los 150 min. b) ¿Cuál es el orden de la cinética del proceso?, c) ¿Cuál es el tiempo en que se ha duplicado la población?, d) ¿En cuanto tiempo se habrá incrementado la población hasta 106 bacterias? e) ¿Cuál es el valor de k? 3. t (min.) # bacterias k0 (#bact/min) k1 (1/min) k2 x 104 (1/#bactmin) 0 100 ------------- 30 200 6.67 0.0231 1.67 60 400 6.67 0.0231 1.25 90 800 8.89 0.0231 0.97 120 1600 13.33 0.0231 0.78 Dado que aquí no tenemos reactivos que se descomponen, sino una población creciente de microorganismos las ecuaciones son: NumBact 1 1 ln − NumBact 100 k0 = k1 = k 2 = 100 NumBact t t t 8.071 a) ln( NumBact ) = ln 100 + (0.023 * 150) = 8.071 NumBact = e = 3,200 b) Es una cinética de primer orden. c) La población se ha duplicado a los 30 minutos (ver tabla datos) 1 100 + 10 6 d) t = ln = 398.63 min k 100 e) k = 0.0231 min-1 1800 1600 1400 n=0 Num Bacterias 1200 1000 800 600 400 200 A B -100 12 R SD 0,93326 0 0 20 40 60 t (min) 80 195,96 2,7 252,98 100 120 0.0 n=1 -0.5 ln(a/a-x) -1.0 -1 k1 = 0.0231 min -1.5 -2.0 -2.5 A B 2.2E-163.3E-16 -0.0231 4.5E-18 R -1 SD 4.25E-16 -3.0 0 20 40 60 80 100 120 t 0.010 n=2 1/ Num Bacterias 0.008 0.006 0.004 0.002 0.000 A B 0,008 0,001 -7,5E-5 1,7E-5 R SD -0,93326 0 0,0016 20 40 60 80 100 120 t (min) 5. La preparación farmacéutica de un jarabe, muestra la siguiente degradación a 55oC. Determine el orden de la descomposición y el tiempo de vida media del producto. t (meses) mg droga/5 ml k0 (mg/meses) ln(mg/5mL) k1 (1/meses) 1/mg k2 (1/mg*meses) τ (meses) 5 37.1 1.143 3.61 0.044 0.027 0.0011 15.77 Se demuestra que la reacción es de orden uno τ = 10 29.8 1.143 3.39 0.044 0.034 0.0012 15.79 0.693 k 20 19.2 2.21 2.95 0.044 0.052 0.0015 15.77 38 36 n=0 34 32 (a-x) 30 28 a= 42.4 mg/5ml 26 24 A B 42,4 -1,2 22 R SD 20 -0,99647 1,3 0,1 1,07 18 4 6 8 10 12 14 16 18 20 22 18 20 22 t 3.7 3.6 n= 1 3.5 ln(a-x) 3.4 ln a= 3.8334 3.3 -1 3.2 k = 0.04392 meses 3.1 3.0 A B 3,8 4,5E-4 -0,044 3,4E-5 R -1 SD 3,7E-4 2.9 4 6 8 10 12 14 t 16 0.055 n=2 0.050 1/(a-x) 0.045 0.040 0.035 A B 0,018 0,002 0,002 1,3E-4 0.030 R SD 0,99702 0,001 0.025 4 6 8 10 12 14 16 18 20 22 t 6. Walker estudió la saponificación del acetato de etilo a 25oC. La reacción es la siguiente: CH3COO2CH5 + NaOH → CH3COONa + C2H5OH. Las concentraciones iniciales de ambos en la mezcla eran 0.10 M. La variación de la concentración de álcali durante 20 min. fué 0.00566 M por lo tanto la concentración residual era 0.00434 M. Calcule la k y el t1/2. En la reacción participan dos reactivos cuyas concentraciones iniciales son iguales por lo que se supone segundo orden. 1 1 − 130.415 1 1 1 k = a−x a = = 6.52 τ= = = 15.33 min t 20 M min ak 0.01 * 6.52 7. Una reacción bioquímica en la carne de pescado es del tipo: S → P Se estudió la cinética de descomposición a concentraciones bajas del sustrato, determinándose una constante de rapidez de 1.035 x 10-5 s-1 a 308 oK ¿Qué porcentaje de una muestra de sustrato se transforma a productos después de 48 horas? Por las unidades de k sabemos que es orden uno como 48 hrs = 172,800 seg ln(a − x) = ln a − kt = ln 100 − (1.035 x10 −5 * 172800) = 2.8167 ( a − x ) = e 2.8167 = 16.7214% Por lo tanto x = 100 − 16.7214 = 83.28% 8. A continuación se proporcionan los datos de concentración y tiempo para la oxidación del ácido láctico. Determine el orden de la reacción y la constante de rapidez. acciónbacteriana t (min.) C (mol/L) k0 x 104 ln(a/a-x) k1 x 104 1/a-x -1/a k2 x 104 0 0.3200 -----0 -----0 ------ 5 0.3175 5.0 0.00784 15.7 0.025 49.2 8 0.3159 5.12 0.0129 16.1 0.040 50.7 10 0.3149 5.10 0.01607 16.1 0.051 50.6 13 0.3133 5.15 0.02116 16.3 0.067 51.4 16 0.3118 5.12 0.02596 16.2 0.082 51.4 Por lo coeficientes de correlación el orden es cero aunque muy cercano al uno Con k= 5.15 x 10-4 (M/min), el método diferencial no da buenos resultados pues los valores de concentración no varían mucho con el tiempo habría que mejorar el experimento. 0.320 n=0 (a-x) 0.318 0.316 0.314 A B 0.32 2.7E-5 -5.15E-4 2.7E-6 R SD -0.99995 0.312 -2 0 2 3.44E-5 4 6 8 10 12 14 16 18 14 16 18 t 0.030 0.025 n=1 0.020 ln(a/a-x) k=0.00163 min -1 0.015 0.010 A B -1.34E-4 0.00163 1.04E-4 1.03E-5 0.005 R SD 0.99992 1.3E-4 0.000 -2 0 2 4 6 8 t 10 12 0.08 n=2 1/(a-x) - 1/a 0.06 0.04 A B 0.02 -5.7E-4 4.1E-4 0.0052 4.007E-5 R SD 0.99988 0.00 -2 0 2 4 6 8 5.1E-4 10 12 14 16 18 t 9. Se sabe que un medicamento es inefectivo cuando se ha descompuesto un 35% del mismo. Si consideramos que la concentración inicial es 5.5 mg/ml y suponemos que la descomposición sigue una cinética de primer orden, calcular el tiempo de expiración y el tiempo de vida media, sabiendo que al analizar el medicamento 20 meses después de preparado, su concentración era 4.2 mg/ml. a ln 0.693 0.27 = 0.0135meses −1 τ= = 51.398meses = 4.28años k = a−x = t 20 k El medicamento expira (es inefectivo) cuando se ha descompuesto un 35% del mismo por tanto (a-x)=65% que corresponden a 3.575 g/mL restantes a ln 0.4308 t exp = a − x = = 31.95meses = 2.66años k 0.0135 10. A 140oC, el régimen de descomposición de una solución acuosa 0.056 M de glucosa, que contiene HCl 0.35 N, se ha encontrado que es como se indica en la tabla de datos. Determine el orden de la reacción y la constante de rapidez. t (h) 0.5 2 3 [Gluc]x 102 (M) 5.52 5.42 5.32 k0 x 103 0 1 2 ln(a/a-x) 0 0.183 0.037 k1 x 103 0 9.1 12.3 1/a-x – 1/a 0 0.33 0.68 k2 0 0.17 0.23 4 5.02 5 0.095 2.4 1.80 0.45 6 4.80 7.2 0.14 2.3 2.72 0.45 8 4.52 10 0.20 2.5 4.00 0.5 12 4.10 14.2 0.30 2.5 6.27 0.52 El orden de reacción es dos sin embargo no es muy seguro, pues están muy cercanos los tres coeficientes de correlación, el método diferencial no da buenos resultados pues los valores de concentración no varían mucho con el tiempo habría que mejorar el experimento. 0.056 n=0 0.054 0.052 (a-x) 0.050 0.048 0.046 0.044 A B 0.06 4.7E-4 -0.00131 7.5E-5 0.042 R SD -0.99193 0.040 0 7.2-4 2 4 6 8 10 12 t n=1 0.30 0.25 ln(a/a-x) 0.20 0.15 0.10 A B -0.026 0.008 0.027 0.001 0.05 R SD 0.99403 0.01 0.00 0 2 4 6 t 8 10 12 7 n=2 6 5 1/a-x - 1/a 4 3 2 A B 1 -0.6 0.57 R SD 0.99436 0 0.2 0.03 0.3 -1 0 2 4 6 t 8 10 12