PROBLEMAS DE CINÉTICA QUÍMICA RESUELTOS. 1. Se aisló una

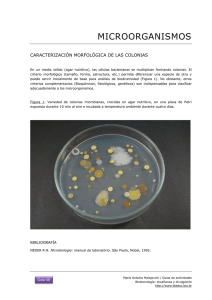
PROBLEMAS DE CINÉTICA QUÍMICA RESUELTOS.
1.
Se aisló una cepa de S. aureus de un producto lácteo contaminado, se resembró en un
medio de Baird Parker e incubó a 35oC durante 48 hrs., después de este tiempo se
contaron 500 colonias, en ese momento se le agregó un antibiótico efectivo contra
este microorganismo y se observó una disminución en el número de colonias.
En las 24 hrs. posteriores a la adición de antibiótico la muerte microbiana presentó
una constante de rapidez de 0.0077 hrs-1. Después de este tiempo se observó un
cambio en el comportamiento cinético del fenómeno y para el mismo cultivo se
determinó una constante de rapidez de 25 colonias/hr hasta la total eliminación de los
microorganismos. Calcule el tiempo en que se eliminaron todos los microorganismos
de este cultivo.
Primeras 24 horas: k= 0.0077 hrs-1 por tanto es orden uno de modo que el número de
colonias después de ese tiempo es:
(a-x) = 415.64 colonias
ln(a − x ) = ln a − kt = ln 500 − 0.0077 * 24 = 6.0298
Las siguientes horas hasta la muerte de todas las colonias, k = 25 Colonias/hr. Por
tanto es orden cero, de manera que el tiempo para que mueran las 415.64 colonias que
había cuando el régimen de orden cero inició es:
a − (a − x) 415.64 − 0
=
t=
= 16.63hr
k
25
Ahora el tiempo para la muerte de las 500 colonias es t= 24 + 16.63 = 40.63 hr
4. Si se ponen 100 bacterias en un matraz de 1 L, con el medio de cultivo apropiado, a una
temperatura de 40oC, encontrará: (Archivo # 63)
a) Prediga el número de bacterias que habrá a los 150 min.
b) ¿Cuál es el orden de la cinética del proceso?,
c) ¿Cuál es el tiempo en que se ha duplicado la población?,
d) ¿En cuanto tiempo se habrá incrementado la población hasta 106 bacterias?
e) ¿Cuál es el valor de k?
t (min.)
# bacterias
k0 (#bact/min)
k1 (1/min)
k2 x 104 (1/#bactmin)
0
100
-------------
30
200
6.67
0.0231
1.67
60
400
6.67
0.0231
1.25
90
800
8.89
0.0231
0.97
120
1600
13.33
0.0231
0.78
Dado que aquí no tenemos reactivos que se descomponen, sino una población creciente de
microorganismos las ecuaciones son:
 NumBact 
1
1
ln

−
NumBact
100

k0 =
k1 = 
k 2 = 100 NumBact
t
t
t
8.071
a) ln( NumBact ) = ln 100 + (0.023 * 150) = 8.071
NumBact = e
= 3,200
b) Es una cinética de primer orden.
c) La población se ha duplicado a los 30 minutos (ver tabla datos)
1 100 + 10 6
ln
= 398.63 min
k
100
e) k = 0.0231 min-1
d) t =
1800
1600
1400
n=0
Num Bacterias
1200
1000
800
600
400
200
A
B
-100
12
R
SD
0,93326
0
0
20
40
60
80
195,96
2,7
252,98
100
120
t (min)
0.0
n=1
-0.5
ln(a/a-x)
-1.0
-1
k1 = 0.0231 min
-1.5
-2.0
-2.5
A
B
2.2E-163.3E-16
-0.0231 4.5E-18
R
-1
SD
4.25E-16
-3.0
0
20
40
60
t
80
100
120
0.010
n=2
1/ Num Bacterias
0.008
0.006
0.004
0.002
0.000
A
B
0,008 0,001
-7,5E-5 1,7E-5
R
SD
-0,93326
0
0,0016
20
40
60
80
100
120
t (min)
5. Se sabe que un medicamento es inefectivo cuando se ha descompuesto un 35% del
mismo. Si consideramos que la concentración inicial es 5.5 mg/ml y suponemos que la
descomposición sigue una cinética de primer orden, calcular el tiempo de expiración y
el tiempo de vida media, sabiendo que al analizar el medicamento 20 meses después de
preparado, su concentración era 4.2 mg/ml. (Archivo 18)
a
ln
0.693
0.27
k = a−x =
= 0.0135meses −1
τ=
= 51.398meses = 4.28años
t
20
k
El medicamento expira (es inefectivo) cuando se ha descompuesto un 35% del mismo
por tanto (a-x)=65% que corresponden a 3.575 g/mL restantes
a
ln
0.4308
t exp = a − x =
= 31.95meses = 2.66años
k
0.0135