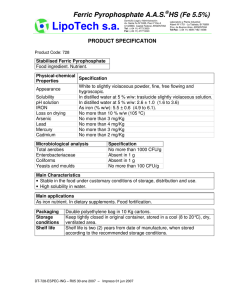
Ex 2- Ternary Phase Diagram Gourav Das 18095 Aim- 1) Determination of the solubility limits in a ternary system of water and two other solvents, one of which is completely miscible and the other is partly miscible with water. 2) Construction of the solubility curve of the system being experimented on triangular graph (ternary) paper. 3) To determine the tie lines of several ternary conjugate solutions of the system being studied. 4) To determine the distribution ratio of the miscible component in the two immiscible phases. Chemicals needed- Water, toluene, Methanol • • • • • • Burette – three units (50 mL volume one unit, 25 mL volume two units), Conical flask (150 mL volume four units), Beakers (100 mL volume two units) Graduated pipette (5 mL volume two units) Funnel (two units) Thermometer (mercury or ethanol) Theory - Several types of solvent that are produced in pharmaceutical formulations. The making of solvent formulation often involve the mixing of multiple component together to have homogenous form. This is usually possible by knowing the exact ratio of each component to be mixed with regard of some other condition such as constant temperature. Following the basis of describing the effect of intensive variable to various phase in a system at equilibrium, which is the phase rule, it is determine that this system have 4 degrees of freedom. The four degrees of freedom are - temperature, pressure, and any two from the three component concentration. F=C–P+2 F=3–1+2 where F refers to Degrees of Freedom; C refers to number of Component F=4 P refers to Phase. In this experiment, there are three components of concern which were Methanol, Toluene and Water. Water is insoluble and toluene, but as it was mixed together with Methanol, all three components can achieve homogeneous solution at equilibrium if proper Fractions were used. Since it is difficult to graphically represent four variables, one variable out of the four is generally considered constant. In this particular experiment , the pressure is considered fixed at 1 atm, and so the number of degrees of freedom becomes three. Any horizontal section of the right-angled prism represents a three-component system under fixed condition of temperature and pressure. For three component systems at constant temperature and pressure, the compositions may be stated in the form of coordinates for a triangular diagram. Procedures 1) Room temperature was measured by using thermometer, which is required to define the phase diagram that will be prepared at the end of this experiment. As this is an equilibrium experiment, temperature must be clearly mentioned. 2) 50 ml Burette was filled with Methanol and 25 ml one are filled with water 3) 5 mL of toluene from the burette and 1 mL of water was added carefully to a clean flask. 4) Methanol was added dropwise from the burette to a clean flask. Make a note of the volume at which a single phase is observed. 5) 1 mL of water was added to that conical flask and repeat step 4 and the volume was noted at which a single phase is observed. 6) the phase diagram for this system was plotted in a ternary plot, assuming no change in volume occurs when these solutions are mixed (ideal liquids, i.e. ΔH0mix = 0) Series Water Toluene Methanol Millimoles VA (mL) VB (mL) VC (mL) nA nB 1 5 12.9 0.05539742 0.045946386 2 5 18.1 0.11079484 0.045946386 3 5 23 0.16619225 0.045946386 4 5 27.1 0.22158967 0.045946386 5 5 31.5 0.27698709 0.045946386 6 5 34.6 0.33238451 0.045946386 1 5 13.7 0.05539742 0.045946386 1 10 19.4 0.05539742 0.091892772 1 15 22.1 0.05539742 0.137839158 1 20 25 0.05539742 0.183785544 1 25 27.2 0.05539742 0.22973193 1 30 30 0.05539742 0.275678316 5 2 24.4 0.27698709 0.018378554 7 2 28.7 0.38778193 0.018378554 10 2 35.3 0.55397418 0.018378554 15 2 46.5 0.83096127 0.018378554 15 1 38.8 0.83096127 0.009189277 40 1 65.2 2.21589673 0.009189277 Total Millimoles nC 0.3188764 0.4474157 0.5685393 0.6698876 0.7786517 0.8552809 0.3386517 0.4795506 0.5462921 0.6179775 0.6723596 0.741573 0.6031461 0.7094382 0.8725843 1.1494382 0.9591011 1.6116854 0.420220209 0.604156953 0.780677966 0.937423699 1.101585162 1.233611794 0.43999549 0.626840752 0.739528711 0.85716049 0.957488898 1.072648768 0.898511713 1.115598684 1.444937006 1.998778029 1.799251674 3.836771398 Molecular Weight (g/mol) XA 0.1318 0.1834 0.2129 0.2364 0.2514 0.2694 0.1259 0.0884 0.0749 0.0646 0.0579 0.0516 0.3083 0.3476 0.3834 0.4157 0.4618 0.5775 Desnsity (g/ml) Molefraction Water Toluene Methanol Water Toluene Methanol XB XC 18.01528 g/mol 92.14 32.04 0.998 0.8467 0.792 0.10933883 0.75883167 0.076050413 0.74056208 0.058854467 0.72826357 0.049013467 0.71460498 0.041709336 0.70684656 0.037245417 0.69331446 0.104424675 0.76967081 0.146596678 0.76502774 0.186387838 0.73870308 0.214412057 0.72095895 0.23993169 0.70221133 0.257007069 0.69134749 0.020454441 0.67127235 0.016474163 0.63592599 0.012719277 0.60389087 0.009194895 0.57507046 0.005107277 0.53305557 0.002395055 0.42006292 Calculation Molecular weight Water = 18.01528, Methanol=32.04, Toluene= 92.14; Here we have to calculate the moles for these three solvents and finally the mole fraction which have to plot in ternary plot. As a example For Water nA= 1/18.01528=0.05539742 For Methanol nB=5/32.04 =0.045946386 For Toluene nc =12.9/ 92.14 = 0.3188764 Sum of all milimoles= nA + nB + nc = 0.420220209 Molefractions For water XA= 0.13183 For Methanol XB = 0.10933883 For Toluene Xc = 0.75883167 Sl No 1 2 3 4 5 %VA %VB %VC mole fraction of Solvents (water) (toluene) (methanol) Xa Xb Xc 70 15 15 0.7 0.15 0.15 15 70 15 0.15 0.7 0.15 15 15 70 0.15 0.15 0.7 33 33 33 0.333333 0.333333 0.333333 50 50 0 0.5 0.5 0 Phases single single single single single As we have got all the given % volume and its Mole fraction based on this we can compare with our data and we can see that all the proportions are lying under the curve means having single phase between three solvents Result All the solvents are having single phase composition upon verifying through ternary phase diagram Conclusion Phase Diagrams are graph for of the liquid, vapour, and solid phases that present at various ranges of temperature and pressure within a reservoir. A ternary phase diagram shows the phase Character of mixtures containing three components in a triangular diagram. This experiment of ternary system involve three different liquids which are Methanol, toluene, and water and is represented using a triangle plot (ternary phase diagram). In this experiment, as the number of volume of Methanol by percentage increase while the number of volume of toluene by percentage decrease, the volume of water will increase. The two separate phase system was established once the cloudiness was observed. This shows that water and toluene are only slightly miscible whereas Methanol is completely miscible with both toluene and water. In the nutshell, the objectives of the experiment are achieved. The solubility limits in a ternary system of water and two other liquids (Methanol and toluene) are determined. The concept of construction of the solubility curve of the system being studied on triangular diagram and concept of miscibility and phase diagram for threecomponent system are understood. Lastly, Phase Rule are used to relate to the use of triangular coordinates to know the mutual solubility of liquids in a two separate phase system.