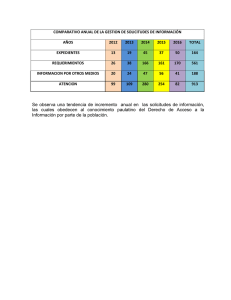
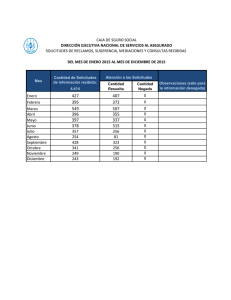
EJERCICIOS SISTEMA DE COLA (M/M/1) 1. El escritor de referencias de una biblioteca universitaria recibe solicitudes de ayuda. Suponga que pueden usarse una distribución de probabilidad de poisson con una tasa media de 10 solicitudes por hora para describir el patrón de llegada y que los tiempos tasa media de 12 solicitudes por hora. a. ¿Cuál es la probabilidad de que no haya solicitudes de ayuda en el sistema? b. ¿Cuál es la cantidad promedio de solicitudes que esperaran por el servicio? c. ¿Cuál es el tiempo de espera promedio en minutos antes de que comience el servicio? d. ¿Cuál es el tiempo promedio en el escritorio de referencias en minutos (tiempo de espera más tiempo de servicio)? Solución: λ = 10 µ = 12 a) b) c) Giusty Guerrero De La Hoz – Ing. Industrial d) e) 2. Movies Tonight es un establecimiento típico de renta de videos y de DVD para clientes que ven películas en su casa. Durante las noches entre semana, los clientes llegan a Movies Tonight a una tasa promedio de 1,25 clientes por minuto. El dependiente del mostrador puede atender un promedio de 2 clientes por minuto. Suponga llegadas de poisson y tiempos de servicio exponenciales. a. ¿Cuál es la probabilidad de que no haya clientes en el sistema? b. ¿Cuál es el tiempo promedio de clientes que esperan por el servicio? c. ¿Cuál es el tiempo promedio que espera un cliente para que comience el servicio? d. ¿Cuál es la probabilidad de que un cliente que llega tenga que esperar por el servicio? e. ¿las características operativas indican que el sistema de mostrador con un solo dependiente proporciona el servicio aceptable? Solución: λ = 1,25 clientes/ minuto µ = 2 clientes/ minuto Giusty Guerrero De La Hoz – Ing. Industrial a) b) c) d) e) Es aceptable que un cliente espere 0,833 minutos o 50 segundos. 3. Speedy Oil proporciona un servicio de un solo canal de cambo de aceite y lubricante de automóviles. Las llegadas nuevas ocurren a una tasa de 2,5 automóviles por hora y la tasa media de servicio es de 5 automóviles por hora. Suponga que las llegadas siguen una distribución de probabilidad de Giusty Guerrero De La Hoz – Ing. Industrial poisson y que los tiempos de servicio siguen una distribución de probabilidad exponencial. a. ¿Cuál es la cantidad promedio de automóviles en el sistema? b. ¿Cuál es el tiempo promedio que espera un automóvil que comience el servicio de aceite y lubricación? c. ¿Cuál es el tiempo promedio que pasa un automóvil en el sistema? d. ¿Cuál es la probabilidad de que una llegada tenga que esperar por el servicio? Solución: λ = 2,5 auto/hora µ = 5 auto/hora a) b) Giusty Guerrero De La Hoz – Ing. Industrial c) d) Giusty Guerrero De La Hoz – Ing. Industrial