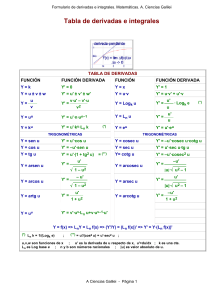
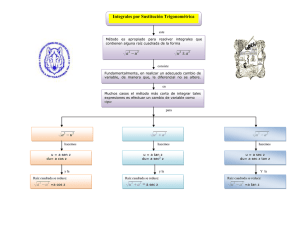
Unidad 3 Trigonometría Reducción al primer cuadrante Si conocemos las razones trigonométricas de un ángulo que está en el primer cuadrante podemos conocer también las razones trigonométricas inversas de otros ángulos relacionados con él. Si por ejemplo cos α = sec(π − α) = 1 1 4 = = − sec α = − cos(π − α) − cos α 5 cosec( −α ) = 1. 4 , entonces: 5 cotg( π 1 1 3 − α) = = = tg α = 2 tg(90 − α ) cotg α 4 1 1 4 3 = = −cosec α = − 1 − ( ) 2 = − sen( −α ) − sen α 5 5 Fíjate en los ejemplos y completa esta tabla. secante 180o −α cosecante cotangente −sec α −α −cosec α 90º − α tg α 360º − α 180º + α 2. Expresa la medida de cada ángulo en radianes, relaciónalo con uno del primer cuadrante cuyas razones conozcas, y rellena la tabla con sus razones trigonométricas: Medida Radianes 120º 2π 3 Ángulo 1.er cuadrante seno coseno tangente secante cosecante cotangente 135º 150º 210º 225º 240º 300º 315º 330º 3. Calcula el valor de las siguientes razones trigonométricas: 9π 4 a) sen 540º c) cos 390º e) tg 750º g) sec b) cotg 630º d) sen 1380º π f) cos − 4 h) cotg (−150º) Unidad 3│Trigonometría i) cosec 2190º j) sec 1260º Matemáticas I 1.º Bachillerato