GUIA DE NOVENO

INSTITUCION EDUCATIVA
TÉCNICO COMERCIAL SAN JUAN
BAUTISTA
MUNICIPIO EL CHARCO - NARIÑO
Nombre:_____________________________
Grado: _________
Asignatura: matemáticas
Docente:KellyYohanaMorenoAsprilla
TEMA: conjuntos numéricos
ESTÁNDAR:
Resuelvo problemas y simplifico cálculos usando
propiedades y relaciones de los números reales y
de las relaciones y operaciones entre ellos
INDICADORES DE DESEMPEÑO:
SABER:
 Identifica las características que definen
los diferentes conjuntos numéricos
 Reconoce las diferentes representaciones
de los números reales.
 Enuncia las propiedades de la suma y el
producto en los números reales.
 Reconoce la notación del valor absoluto.
 Reconoce la notación de la potenciación.
 Reconoce la notación de la radicación.
HACER:
 Clasifica los números reales de acuerdo
con sus características
 Ubica los números en la recta real.
 Resuelve problemas que involucran sumas
y productos de números reales
 Analiza situaciones que involucran el valor
absoluto.
 Aplica el concepto de la potenciación.
 Aplica el concepto de la radicación.
 Aplica el concepto de la logaritmación.
SER:
 Muestra compromiso y responsabilidad en
la formación de su vida y en el área
 Demuestra responsabilidad con trabajos,
talleres, tareas, y consultas asignad
INSTRUCCIONES: Leo mentalmente la guía de trabajo, pienso y
analizoelcontenidodadoydesarrolloel taller indicado.
CONJUNTOSNUMÉRICOS
Los matemáticos reconocen varios conjuntos de
números que comparten ciertas características.
Estas categorías son útiles cuando ciertos tipos de
números son válidos para valores y variables.
Nuestro entendimiento y clasificación de los
diferentes conjuntos de números se ha
desarrollado durante miles de años.
DEFINICIÓN:
Los conjuntos numéricos
son
agrupaciones de números que guardan una serie
de propiedades estructurales. Por ejemplo, el
sistema más usual en aritmética natural está
formado
por
el conjunto
de
los
números naturales, con la suma, la multiplicación
y las relaciones usuales de orden aditivo.
CONJUNTOS DE LOS NÚMEROS NATURALES (N)
Los números naturales se pueden representar en
una recta ordenados de menor a mayor.
Sobre una recta señalamos un punto, que
marcamos
con
el
número
cero (0).
A la derecha del cero, y con las mismas
separaciones, situamos de menor a mayor los
siguientes números naturales: 1, 2, 3…
Suma de números naturales:
a+b=c
Los términos que intervienen en una suma se
denominan sumandos. Por lo tanto, a será un
sumando y b será otro sumando.
El resultado (c) se denomina suma.
PROPIEDADES DE LA SUMA
 Asociativa
El modo de agrupar los sumandos no varía el
resultado.
(a + b) + c = a + (b + c)
Ejemplo:
(2 + 3) + 5 = 2 + (3 + 5)
5+5=2+8
10 = 10
 Conmutativa
El orden de los sumandos no varía la suma.
a+b=b+a
Ejemplo:
2+5=5+2
7=7
RESTA DE NÚMEROS NATURALES:
a−b=c
Los términos que intervienen en una resta se
denominan minuendo (a), sustraendo (b)
y diferencia (c).
MULTIPLICACIÓN DE NÚMEROS NATURALES:
Los términos de la multiplicación se
denominan factores (a) y (b), y producto (c) el
resultado. a x b = c
Multiplicar dos números naturales consiste en
sumar uno de los factores consigo mismo tantas
veces como indica el otro factor.
Por ejemplo, la multiplicación (2·5) consiste en
sumar el número 2 cinco veces.
2+2+2+2+2 = 10 ⇒ 2 x 5 = 10
PROPIEDADES DE LA MULTIPLICACIÓN:
 Asociativa
El modo de agrupar los factores no varía el
resultado.
(a · b) · c = a · (b · c)
Ejemplo:
(2 · 3) · 5 = 2 · (3 · 5)
6 · 5 = 2 · 15
30 = 30
 Conmutativa
El orden de los factores no varía el producto.
a·b=b·a
Ejemplo:
2·5=5·2
10 = 10
 Distributiva
La multiplicación de un número natural por una
suma es igual a la suma de las multiplicaciones de
dicho número natural por cada uno de los
sumandos.
a · (b + c) = a · b + a · c
Ejemplo:
2 · (3 + 5) = 2 · 3 + 2 · 5
2 · 8 = 6 + 10
16 = 16
 Sacar factor común
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común,
podemos transformar la suma en producto
extrayendo dicho factor.
a · b + a · c = a · (b + c)
Ejemplo:
2 · 3 + 2 · 5 = 2 · (3 + 5)
6 + 10 = 2 · 8
16 = 16
DIVISIÓN DE NÚMEROS NATURALES:
TIPOS DE DIVISIÓN:
DIVISIÓN EXACTA: una división es exacta cuando
el resto es cero.
15:5 = 3 de resto 0
División entera: una división es entera cuando el
resto es distinto de cero.
19:5 = 3 de resto 4
Se deja el mismo exponente y se multiplican las
bases
23 · 43 = (2 · 4)3=83
DIVISIÓN DE POTENCIAS CON EL MISMO
EXPONENTE Y DIFEENTE BASE
Se deja el mismo exponente y se dividen las bases.
63 : 33 = (6:3)3 = 23
LOGARITMO
Se define logaritmo como el exponente de una
potencia con cierta base, es decir, el número al cual
se debe elevar una base dada para obtener un
resultado determinado.
POTENCIAS DE NÚMEROS NATURALES:
Una potencia es una forma abreviada de escribir un
producto formado por varios factores iguales.
5 · 5 · 5 · 5 = 54
Los elementos que constituyen una potencia son:
La base de la potencia es el número que
multiplicamos por sí mismo, en este caso el 5.
El exponente de una potencia indica el número de
veces que multiplicamos la base, en el ejemplo es
el 4.
Cualquier número elevado a 0 es igual a 1.
502° = 1
Cualquier número elevado a 1 es igual a sí mismo.
19¹ = 19
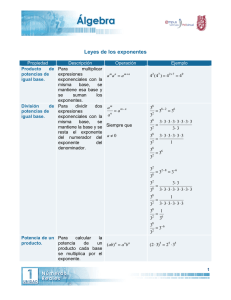
PRODUCTO DE POTENCIAS CON LA MISMA BASE
Se suman los exponentes.
25 · 22 = 25+2 = 27
DIVISIÓN DE POTENCIAS CON LA MISMA BASE
Se restan los exponentes.
25 : 2 2 = 25 − 2 = 23
Por ejemplo:
50=1
51 = 5
52 = 25
53 = 125, etc.
Luego, siendo la base 5, el logaritmo de 1 (que se
escribe log5 1) es 0, por que 0 es el exponente al
que hay que elevar la base 5 para que dé 1; el
log5 5 es 1; el log5 25 es 2, el log5 125 es 3, etc.
- No existe el logaritmo de los números
negativos.
POTENCIA DE UNA POTENCIA
Se multiplican los exponentes.
(25)3 = 215
- El argumento y la base de un logaritmo son
números reales positivos. Además, la base no
puede ser 1. Es decir, en la expresión logb a,
siempre, por definición, a ∈ R+ y b ∈ R+ – {1}.
PRODUCTO DE POTENCIAS CON EL MISMO
EXPONENTE Y DIFERENTE BASE
- La expresión logb a , se lee como: “logaritmo de
a en base b”.
Volvamos a la definición de logaritmo:
“exponente al que es necesario elevar una
cantidad positiva para que resulte un número
determinado”.Si lo escribiera como ecuación,
corresponde a resolver logb a = x, donde b es la
base del logaritmo y aes su argumento, con a y b
positivos.
logb (1) = 0 ; con b ≠ 1.
50 =1
Ej: log5 (1) = 0 porque
log7 (1) = 0 porque 70 = 1
log20 1 = 0 ⇔ 200 = 1
Ejemplo1:
LOGARITMOS DE LA BASE
- Calcula el valor de log7 343
El logaritmo de la base es igual a 1.
equivale a resolver la ecuación:
log7 343 = x
Entonces, ya que la base del logaritmo es 7, el
exponente no se conoce y 343 es el argumento, es
decir, el valor de la potencia, se puede escribir:
7x =343
7x = 73
luego, igualando los exponentes, se concluye que
x= 3
Luego, log7 343 = 3
Ejemplo 2:
- Calcula el valor de log0,7 0,343
equivale a resolver la ecuación:
log0,7 0,343 = x
Luego:
0,7x = 0,343
0,7x = (0,7)3
Luego, igualando exponentes tenemos:
x=3
log0,7 0,343 = 3
Para una definición más completa de logaritmos,
se determinarán restricciones respecto de su base
y su argumento.
PROPIEDADES
logb (b) = 1 ; con b ≠ 1.
Ej:
log5 (5) = 1 ⇔ 51 = 5
log6 (6) = 1 ⇔ 61 = 6
log12 (12) = 1 ⇔ 121 = 12
LOGARITMO DE UNA POTENCIA CON IGUAL
BASE:
El logaritmo de una potencia de un número es igual
al producto entre el exponente de la potencia y el
logaritmo del número.
logb bn = n, con b ≠ 1
Ej:
log6 6 3 = 3
LOGARITMO DE UN PRODUCTO
El logaritmo de un producto es igual a la suma de
los logaritmos de los factores.
logb (a • c) = logb a + logb c
Ej:
logb (5 • 2) = logb 5 + logb 2
Calcula cada uno de los siguientes logaritmos
a) log2 64
g) log128 1
b) log5 1
h) log6 6 3
LOGARITMO DE LA UNIDAD
c) log3 3
El logaritmo de 1 en cualquier base es igual a 0.
d) log5 5 7
RAÍZ CUADRADA DE NÚMEROS NATURALES:
La radicación es la operación inversa a la
potenciación.
Consiste
en:
dados
dos
números,
llamados radicando e índice, hallar un tercero,
llamado raíz, tal que, elevado al índice, sea igual al
radicando.
(Raíz)índice = Radicando
5² = 25
En la raíz cuadrada el índice es 2, aunque en este
caso se omite, es decir, no se pone el 2.
√25 = 5



El índice es 2 (por eso no se pone)
El radicando es 25
La raíz es 5
OPERACIONES CON RAÍCES
Las operaciones con radicales nos ayudan a
conseguir la mayor simplificación de la raíces hasta
el punto de encontrar su resultado o expresarla de
la forma más sencilla posible.
Para poder resolver operaciones con raíces, es
necesario
conocer
en
qué
consisten las propiedades de los radicales. Aquí
puedes encontrar algunos ejercicios resueltos de
operaciones con radicales para que puedas
comprender perfectamente los pasos a realizar en
cada una de ellas.
SUMA DE RAÍCES
Cuando sumamos raíces, sólo podemos sumar
radicales que sean semejantes. Esto significa que
solamente se pueden sumar radicales que posean
el mismo índice y el mismo radicando.
En el caso de que queramos sumar radicales
semejantes se suma la parte que encontramos
fuera del radical, que se encuentra multiplicando al
radical, y se mantiene el mismo radicando. Cuando
no encontramos ningún número fuera de la raíz es
como si hubiera un 1.
RESTA DE RAÍCES
Para realizar la resta de radicales debemos seguir
el mismo proceso que en la suma. Debemos restar
la parte de fuera y mantener el mismo radical.
Recuerda que si no encontramos ningún número
fuera de la raíz es igual a 1.
MULTIPLICACIÓN DE RAÍCES
Las propiedades de los radicales nos muestran
que la multiplicación de radicales es igual a la raíz
del producto de cada uno de los factores. Por ello,
para realizar el producto de radicales debemos
multiplicar cada uno de los radicandos y colocarlos
bajo el mismo radical.
DIVISIÓN DE RADICALES
Al igual que en el caso anterior, en el cociente de
radicales es igual al radical del cociente de
radicandos. De esta forma, para realizar división
de raíces debemos dividir los números que se
encuentran dentro de las raíces y colocar el
resultado dentro de un mismo radical.
OPERACIONES COMBINADAS:
ORDEN QUE HAY QUE SEGUIR PARA RESOLVER
COMBINADAS
1. Efectuar las operaciones entre paréntesis,
corchetes y llaves.
2. Calcular las potencias y raíces.
3. Efectuar los productos y cocientes.
4. Realizar las sumas y restas.
(15 − 4) + 3 − (12 − 5 · 2) + (5 + 16: 4) − 5 + (10
− 22) =
=11 + 3 – (12 – 10) + (5 + 4) – 5 + (10 – 4) =
=11 + 3 -2 + 9 – 5 + 6 =
= 22
Realizamos en primer lugar las operaciones que
están dentro de los paréntesis, respetando el
orden de prioridad.
Quitamos paréntesis realizando las operaciones.
a.
b.
c.
EJERCICIOS
A. 8 − 6 + 7 − 5 − 2 + 8 − 6 =
B. 4 · 3 − 8 + 7 · 2 − 10 + 2 · 6 =
C. 6· 3 − 12 : 2 + 7 − 4 · 3 =
D. 3² − 4 · 2 + 18 : 3 + 24 − 42 =
E. (13 − 4 · 2) − 4 + (2 · 6 − 7) − (14 − 3²) =
F. [3³ − (4 · 3 + 8)] − (3 · 6 − 15) + 22 – (8 − 6) =
G. 8² − [(12 : 2) · (24 : 6)] − {25 − [24 − (18 : 3)]} =
SUMA DE NÚMEROS ENTEROS
(32)2 – 11 · √4 =
5 + √(43 + √36) =
38 – [15 – (8 – 3) – 7] =
Si los signos son diferentes, se resta y se pone el
signo del número que tenga el mayor valor
absoluto:
CONJUNTO DE LOS NÚMEROS ENTEROS
Si los signos son iguales, se suma y se mantiene el
signo:
+++=+
−+−=−
→
6 + 6 = 12 POSITIVO
→ -6+(-6)=-12 NEGATIVO
6 + (-3) = 3 POSITIVO porque el número 6 es más
grande que el 3 y se pone su signo.
-6 + 3 = -3 NEGATIVO porque el número 6 es más
grande que el 3 y se pone su signo.
RESTA DE NÚMEROS ENTEROS
(no naturales o enteros negativos) (cero)
(naturales o enteros positivos)
El símbolo de la resta le cambia el signo a la cifra
que le sigue y la resta pasa a ser una suma, es
decir, el -3 pasa a ser +3 y la resta pasa a ser una
suma.
EL VALOR ABSOLUTO, ES UN NÚMERO SIN
SIGNO, ES DECIR, EL VALOR ABSOLUTO DE:
6 – (-3) = 6 + (+3) = 9 POSITIVO
POTENCIA DE NÚMEROS ENTEROS
-8 → 8
(+) elevado a par= +
72→ 72
MULTIPLICACIÓN DE NÚMEROS ENTEROS
+×+=+
−× − = +
→
5 × 3 = 15 POSITIVO
→ −5×(−3)= 15 POSITIVO
+×−=−
→
−× + = −
→ −5×(−3)= −15 NEGATIVO
(-) elevado a par = +
(+) elevado a impar = +
(-) elevado a impar = –
5×(−3)= −15 NEGATIVO
DIVISIÓN DE NÚMEROS ENTEROS
+:+=+
→
6 : 3 = 2 POSITIVO
−: − = +
→ −6:(−3)= 2 POSITIVO
+:−=−
→ 6 :(−3)=−2 NEGATIVO
−: + = −
→
−6: 3 = −2 NEGATIVO
La potencia de 0 es 1.
a0 =1
(− a)0 =1
La potencia con exponente negativo es su inversa
positiva.
Producto con la misma base → se mantiene la
base y se suman los exponentes.
4².4³ = 4²+³
División con la misma base → se mantiene la base
y se restan los exponentes.
4³ : 4² = 4³¯² = 4
Potencia de una potencia → se mantiene la base y
se multiplican los exponentes.
(4³)² = 4³·²
Producto con diferentes bases y mismos
exponentes → se multiplican las bases y se
mantiene el exponente.
23 · 43 = (2 · 4)3=83
a) 10 grados bajo cero
b) Tercer sótano
c) 3 metros bajo el nivel del mar
d) 12 grados bajo cero
CONJUNTO DE LOS NUMEROS RACIONALES
El conjunto de los números racionales se designa
por la letra Q., y corresponde a la definición de un
número entero dividido por otro.
DIVISIÓN CON DIFERENTES BASES Y MISMOS
exponentes → se dividen las bases y se mantiene
el exponente.
63 : 33 = (6:3)3 = 23
Ejercicios
1.Suma las siguientes operaciones:
(+5)+(+3)=
(–8)+(–5)=
(–3)+(+9)=
(- 2 ) + ( – 15) =
(–4)+(–4)=
(–1)+(+7)=
(–5)+(+0)=
(–5)+(+5)=
2. Resta las siguientes operaciones:
(–8)–(+0)=
(–5)–(+5)=
(–3)–(+9)=
(–8)–(–5)=
3. Clasifica los siguientes números en positivos y
negativos:
+3
-5
+7
-9
+32
-6
25
-14
+345
-89
4.Expresa con números negativos las siguientes
expresiones:
 p

/ p, q  Z , q  0 
 q

Q= 
Las propiedades en el conjunto de los números
racionales son las siguientes:
a) es infinito,
b) no tiene primer ni último elemento.
c) entre dos números racionales, siempre existe
otro número racional, por ejemplo. Es decir, el
conjunto es DENSO.
d) está ordenado por la relación “menor o igual”
e) se cumple la propiedad de tricotomía. (Entre dos
números, se puede comparar con una
sola de las siguientes relaciones: “mayor”,
“menor” o “igual”.)
FORMAS DE EXPRESAR UN RACIONAL.
Existen tres formas de expresar un número
racional:
a)
p
tal que
q
q0
(forma de racional fraccionario)
a
3
=a:b
Ej. : = 3 : 4 = 0,75
b
4
( forma de racional decimal )
b)
ar
3 3  25 75
/ b  r = 100
Ej. : =
=
= 75 %
br
4 4  25 100
(racional porcentual)
c)
FORMAS DE UN RACIONAL DECIMAL.
Existen tres formas de expresar un racional
decimal:
30. Encuentra:
a)
2
1
de
de 12
3
2
b)
5
1
de
de 108
6
9
31.Intercala cinco decimales entre:
-
a) racional finito o exacto
a
b
a:b  c
tal que
Ejemplo :
a ) 0, 4 y 0,5
con resto cero
2
 0,4
5
_
b) 1,2 3 y 1, 2
OPERACIONES EN Q.
NOCIÓN : Propiedades de las operaciones en el
sistema ( Q, +, · )
b) racional infinito periódico
b)
En Q se definen las dos siguientes operaciones:
SUMA Y RESTA DE NÚMEROS
RACIONALES
c) racional infinito semiperiodo
Con el mismo denominador
PROPIEDADES DE LA IGUALDAD Y DESIGUALDAD
DE FRACCIONES
Si
a
b
a
b
y
=
c
d
c
d
>
ad
entonces
entonces
Se suman o se restan los numeradores y
se mantiene el denominador.
= b c
ad
> b c
Ejemplos:
EJERCICIOS.
27. Señala si las siguientes parejas de racionales
son iguales:
a)
2
4
y
3 7
b)
-2
-6
y
9
3
28. Indica el signo >, < o = que corresponda
en las siguientes parejas de racionales :

2
1
a)
b) 5 y 4
y
7
6
8
7

4
12
c)
y 9
27
29. Encuentra el valor de x en las siguientes
igualdades:
a)
4
x
=
8
2
b)
20
5
=
16
x
-
c)
13
x
=
26
2
-
d)
1
3
=
2
x
c)
-2
8
y
5
20
Con distinto denominador
En primer lugar, se reducen los
denominadores a común denominador, y
se suman o se restan los numeradores de
las fracciones equivalentes obtenidas.
Ejemplos:
1.
MULTIPLICACIÓN DE NÚMEROS
RACIONALES
El producto de dos números racionales es
otro número racional que tiene:
1.
2.
3.
1 Obtenemos el numerador por el
producto de los numeradores.
4.
2 Obtenemos el denominador por el
producto de los denominadores.
5.
Ejemplo:
NÚMEROS IRRACIONALES (Q’)
DIVISIÓN DE NÚMEROS RACIONALES
La
división
de
dos númer os
racionales es otro número r acional que
tiene:
Por numerador el producto de los
extremos.
Por denominador el producto de los
medios.
También podemos definir la divisió n de
dos números racionales como producto
del primero por el inv erso del
segundo.
EJERCICIOS.
Resuelve los siguientes ejercicios
Como vimos antes, si un número tiene una
cantidad finita de cifras decimales o tiene infinitas
cifras decimales periódicas es un número racional.
Pero podemos escribir números que, aunque
tienen infinitas cifras decimales, éstas no son
periódicas, por ejemplo:
0,1234567891011121314151617181920…
(las
cifras decimales son la sucesión de los números
naturales);
0,1011001110001111000011111…..
(las cifras decimales son una sucesión de un uno y
un cero, luego, dos unos y dos ceros, tres unos y
tres ceros, etc.)
Estos números no son racionales pues es imposible
encontrar un período y por lo tanto no se pueden
escribir como fracción ordinaria, los llamaremos
irracionales.
Llamamos conjunto de números irracionales a los
números decimales que tienen infinitas cifras no
periódicas, no se pueden expresar como el
cociente entre dos números enteros.
Ejemplos de números irracionales:
Todas las raíces inexactas son números
irracionales. el PI π = Es el número de veces que el
diámetro de una circunferencia cabe en el
perímetro de dicha circunferencia. Se aproxima a
3,14
Se pueden inventar decimales infinitos no
periódicos mediante azar o secuencias numéricas.
El número e se aplica a problemas de intereses y de
crecimiento exponencial.
e = 2,71828182845904523… se aproxima a 2,7
CONJUNTOS DE LOS NÚMEROS REALES(R)
Entre los racionales y los irracionales se completa
la recta numérica. Es decir, ya no queda ningún
punto sobre la recta al que no le corresponda ya
sea un número racional o un número irracional. Es
por ello que se considera que, si se unen los dos
conjuntos, esto es, Racionales más Irracionales se
forma un nuevo conjunto
La unión de los números racionales con los
números irracionales constituye el conjunto de
los números reales.
Simbólicamente: R = {….- 10, -1, – ¾, – ½, – ¼, 0, ¼
, √2, 5 , …..} R= {Q U Q’}
Propiedades del conjunto de los números reales


Es un conjunto infinito.
No existe un primer ni un último número
real.
Las dos propiedades más importantes son:
Propiedad de densidad de los números reales, y
propiedad de la representación gráfica.
El conjunto de los números reales es denso, es
decir que entre dos números reales existen
infinitos números reales.
Ejemplo: de 3.1 para llegar a 3.2 podemos pasar
por infinitos números 3.11, 3.12, 3.13, 3.1999 etc.
CONJUNTOS DE LOS NÚMEROS IMAGINARIOS(I)
¿Por qué surgen los números imaginarios?
Surgen por la necesidad de obtener las raíces de
índice par de cantidades negativas. Se denotan
por i. La unidad de los números imaginarios es la
raíz cuadrada de – 1 y se denota por i, así que: i = √1.
Debes
tener
en
cuenta:
i2 = -1, i 3 = – i, i 4 = 1.
Pues bien, un número
complejo es simplemente
dos números sumados
juntos (uno real y uno
imaginario).
Cero
NÚMEROS COMPLEJOS
Un número complejo es una combinación de
un número real y un número imaginario
La
unión
de
los
números reales con
los imaginarios da
origen
a
los números complejos denotados por C.
Ejemplos:
1+i
12 - 3.1i -0.85 - 2i
π + πi
√2 + i/2
¿Un número que es una combinación de dos
números?
¿Puedes hacer un número
combinando a partir de
otros dos? ¡Claro que
puedes!
Lo haces todo el tiempo en
las fracciones. La
fracción 3/8 es un número
hecho de un 3 y un 8.
Sabemos que significa "3 de
8 partes iguales".
Entonces, un número complejo tiene una parte
real y una parte imaginaria.
Pero cualquiera de las dos puede ser 0, así que los
números reales y los imaginarios son también
números complejos.
Número
complejo
Parte real
Parte
imaginaria
3 + 2i
3
2
5
5
0
-6i
0
-6
Sumar y multiplicar
Para sumar dos números complejos
sumamos las dos partes por separado:
(a,b) + (c,d) = (a+c, b+d)
Ejemplo: (3 + 2i) + (1 + 7i) = (4 +
9i)
Pero para multiplicarlos seguimos una regla
más interesante:
(a,b)(c,d) = (ac-bd, ad+bc)
Ejemplo: (3 + 2i)(1 + 7i) = ((3×1 2×7) + (3×7 + 2×1)i) = -11 + 23i
Puedes intentarlo tú mismo: escribe (3 +
2i)(1 + 7i) en la calculadora de números
complejos.
Y una cosa interesante es que el cuadrado
de "i" sí que es -1
Ejemplo: (0 + i)(0 + i) = ((0×0 1×1) + (0×1 + 1×0)i) = -1 + 0i
ACTIVIDADES DE CONSTRUCCIONES
Lema.
“Educando con amor y creciendo en Sabiduría”
Prof. Kelly Yohana M.A.