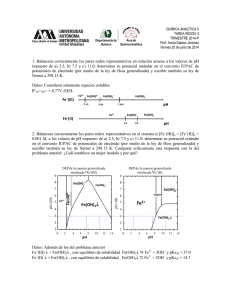
Calcular los números de transporte correspondientes al
Anuncio

DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS FUNDAMENTOS DE ANÁLISIS INSTRUMENTAL. 5ª RELACIÓN DE PROBLEMAS. 1.- Calcular los números de transporte correspondientes a los iones Cl- y H+: a) En una disolución acuosa de HCl 0.1 M. b) En una disolución acuosa de HCl y CaCl2 0.1 M. Datos: Conductividades equivalentes: Cl- = 76 ; H+ = 350 ; Ca2+ = 59.5. Solución: tH+=0.82, tCl-=0.18; tH+=0.50, tCl-=0.33, tCa2+=0.17 2.- Calcular los números de transporte correspondientes a los iones Fe(CN)63- y Fe(CN)64- a) en una disolución acuosa que contiene K3Fe(CN)6 10–4 M y K4Fe(CN)6 10–4 M. b) Suponer que a dicha disolución se le añadió KNO3 hasta 0.1 M. c) Suponer que a dicha disolución se le añadió La2(SO4)3 0.1 M. Datos: Conductividades equivalentes (mho cm2 equiv-1): Fe(CN)63- = 100.0; Fe(CN)64- = 110.0; SO42– = 80.0; NO3– = 71.5; K+ = 73.4; La3+ = 69.6 -3 -3 -4 -4 Solución: tFe(CN)63-=0.24,tFe(CN)64-=0.35;tFe(CN)63-=2.05x10 ,tFe(CN)64-=3.01x10 ;tFe(CN)63-=3.34x10 tFe(CN)64-=4.90x10 3.- Una disolución acuosa contiene FeCl3 10-4 M y FeSO4 10-4 M. Se introducen dos electrodos de platino, estableciéndose entre ellos una determinada diferencia de potencial y obteniéndose, como consecuencia, una corriente eléctrica de 95 μA. Determinar las intensidades de migración que corresponden a los iones Fe3+ y Fe2+ en el cátodo y ánodo, respectivamente. a) Suponer que a la disolución inicial se le añadió KCl hasta 0.1 M. b) Calcular el error que se comete, al operar en las condiciones inicialmente descritas, si se supone que la corriente detectada en el amperímetro se debe totalmente a transporte por difusión, en el caso de que el experimento se utilizara para la determinación cuantitativa de Fe3+. Datos: Conductividades equivalentes: Fe3+ = Fe2+ = 68; SO42- = 80; K+ = 73.5; Cl- = 76. Solución: IM(Fe3+)=8.86 µA, IM(Fe2+)=9.02 µA; IM(Fe3+)=0.044 µA, IM(Fe2+)=0.0432 µA; 10.3 % 4.- Se quiere determinar Fe2+ en disoluciones que contienen del orden de 10–3 M de dicho catión. Dichas disoluciones contienen, además, cloruros y sulfatos en concentración similar a la del hierro. El método de análisis se basa en la medida de corrientes límite de difusión. a) ¿Qué concentración de electrolito fondo (KCl) debe añadirse para que el error de los resultados sea inferior al 3 %? b) Si se obtuvieron corrientes del orden de 50 µA, utilizando un electrodo de platino de superficie eficaz 1.43 mm2. ¿Cuál será el espesor de la interfase si el coeficiente de difusión del Fe2+ es aproximadamente 2.8x10-5 cm2/s? Datos: Conductividades equivalentes: Fe2+ = 68; SO42– = 80 ; K+ = 73.5 ; Cl– = 76. -3 -4 Solución: [KCl]=12.22x10 M; δ=7.73x10 cm 5.- Construir las curvas I-E de los siguientes ejemplos prácticos: a) Disolución de Fe2+ 0.1 M y de Fe3+ 0.05 M a pH=0 y a pH=2, con electrodo de Pt y calomelanos. b) Disolución de Fe2+ y Ce3+ 0.1 M en las condiciones anteriores. Datos: Eo (Fe3+/Fe2+) = + 0.77 V ; Eo (Ce4+/Ce3+) = + 1.0 V. 6.- Calcular la ecuación de la curva I-E, así como su potencial de semi-onda: a) Para una disolución de Cd2+ 10–3 M. b) Para una disolución de Cd2+ 10–3 M y NH3 1 M. Datos: ß4 (Cd(NH3)42+) = 106.56 , Eo (Cd2+/Cd0) = -0.402 V. E1/2= -0.4994 V; E1/2= -0.693 V DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 7.- Estudiar las curvas de I-E sobre un electrodo de mercurio en el transcurso de la valoración complexométrica de Cd2+ con EDTA. Siendo X ((Y4–)/(Cd2+)) = 0, 0.5, 1 y.2. Datos: Eo (Cd2+/Cd0) = -0.40 V; Eo (Hg2+/Hg0) = 0.86 V; Log Kd (CdY2-) = -16.1; Log Kd (HgY2-) = -20.4 CÁLCULO DEL NÚMERO DE TRANSPORTE Número de transporte 0 λi = conductivdad equivalente del íon ci = concentración del ión Zi = carga del ión en valor absoluto ti = λ0i ci Z i n ∑λ c Z j =1 Intensidad de Migración IT = Intensidad de corriente ti =nº de transporte del ión n = nª de electrones puestos en juego en la electrolisis Z = carga del ión Intensidad total de corriente 0 j j j DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 1.- Calcular los números de transporte correspondientes a los iones Cl- y H+: a) En una disolución acuosa de HCl 0.1 M. b) En una disolución acuosa de HCl y CaCl2 0.1 M. Datos: Conductividades equivalentes: Cl- = 76 ; H+ = 350 ; Ca2+ = 59.5. Solución: tH+=0.82, tCl-=0.18; tH+=0.50, tCl-=0.33, tCa2+=0.17 Teniendo en cuenta la expresión que permite el cálculo de los números de transporte: ti = λ0i ci Z i n ∑λ c Z j =1 0 j j j Se establecen las concentraciones en disolución, tras las disociaciones/equilibrios: HCl → H + i) + Cl − 0.1 →) 0.1 0.1 Se construye la siguiente tabla: λi 349.8 76.3 0 Especie + H Cl |Zi| 1 1 ci 0.1 0.1 λi ci |Zi| 34.98 7.63 0 Σλj cj |Zj| 42.61 42.61 0 ti 0.821 0.179 En el apartado b): HCl → H + i) CaCl2 0.1 i) →) Especie + H Cl 2+ Ca + Cl − 0.1 λi 349.8 76.3 59.5 0 + 2Cl − 0.1 0.2 0.1 →) 0.1 ci 0.1 0.3 0.1 → Ca 2+ |Zi| 1 1 2 λi ci |Zi| 34.98 22.89 11.9 0 Σλj cj |Zj| 69.77 69.77 69.77 0 ti 0.501 0.328 0.171 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 2.- Calcular los números de transporte correspondientes a los iones Fe(CN)63- y Fe(CN)64a) en una disolución acuosa que contiene K3Fe(CN)6 10–4 M y K4Fe(CN)6 10–4 M. b) Suponer que a dicha disolución se le añadió KNO3 hasta 0.1 M. c) Suponer que a dicha disolución se le añadió La2(SO4)3 0.1 M. Datos: Conductividades equivalentes (mho cm2 equiv-1): Fe(CN)63- = 100.0; Fe(CN)64- = 110.0; SO42– = 80.0; NO3– = 71.5; K+ = 73.4; La3+ = 69.6 -3 -3 -4 -4 Solución: tFe(CN)63-=0.24,tFe(CN)64-=0.35;tFe(CN)63-=2.05x10 ,tFe(CN)64-=3.01x10 ;tFe(CN)63-=3.34x10 tFe(CN)64-=4.90x10 a) K 3 Fe(CN ) 6 → + Fe(CN ) 36− 3K + 10 −4 i) →) 3x10 −4 K 4 Fe(CN ) 6 → 10 −4 + Fe(CN ) 64− 4K + 10 −4 i) →) Especie 3Fe(CN)6 4Fe(CN)6 + K 4 x10 −4 λi 100 110 73.5 0 10 −4 |Zi| 3 4 1 ci -4 10 -4 10 -4 7x10 λi ci |Zi| -2 3x10 -2 4.4x10 -2 5.145x10 Σλj cj |Zj| -1 1.2545x10 ti 0.239 0.351 0.410 λi ci |Zi| -2 3x10 -2 4.4x10 7.35 7.15 Σλj cj |Zj| 14.574 ti -3 2.1x10 -3 3.0x10 0.504 0.491 0 0 b) Además de las concentraciones anteriores: i) →) Especie 3Fe(CN)6 4Fe(CN)6 + K NO3 KNO3 0.1 → K+ 0.1 λi 100 110 73.5 71.5 0 + NO3 − 0.1 ci -4 10 -4 10 -4 0.1+7x10 ≅0.10 0.1 |Zi| 3 4 1 1 0 0 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS c) i) →) Especie 3Fe(CN)6 4Fe(CN)6 + K 2+ La 2SO4 La2 ( SO4 ) 3 0.1 → 2 La 3 + + 3SO4 0.2 λi 100 110 73.5 69.6 80 0 ci -4 10 -4 10 -4 7x10 0.2 0.3 2− 0.3 |Zi| 3 4 1 3 2 λi ci |Zi| -2 3x10 -2 4.4x10 -2 5.145x10 41.76 48 0 Σλj cj |Zj| 89.89 0 ti -4 3.3x10 -4 4.9x10 -4 5.7x10 0.465 0.534 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 3.- Una disolución acuosa contiene FeCl3 10-4 M y FeSO4 10-4 M. Se introducen dos electrodos de platino, estableciéndose entre ellos una determinada diferencia de potencial y obteniéndose, como consecuencia, una corriente eléctrica de 95 μA. a) Determinar las intensidades de migración que corresponden a los iones Fe3+ y Fe2+ en el cátodo y ánodo, respectivamente. b) Suponer que a la disolución inicial se le añadió KCl hasta 0.1 M. c) Calcular el error que se comete, al operar en las condiciones inicialmente descritas, si se supone que la corriente detectada en el amperímetro se debe totalmente a transporte por difusión, en el caso de que el experimento se utilizara para la determinación cuantitativa de Fe3+. Datos: Conductividades equivalentes: Fe3+ = Fe2+ = 68; SO42- = 80; K+ = 73.5; Cl- = 76. Solución: IM(Fe3+)=8.87 µA, IM(Fe2+)=8.88 µA; IM(Fe3+)=0.043 µA, IM(Fe2+)=0.043 µA; 10.3 % I T ti n IM = ± Z ∑λ c Z 0 + j j j 3Cl − 10 −4 →) 10 −4 FeSO4 i) n j =1 → Fe 3+ FeCl3 i) ti = λ0i ci Z i 3x10 −4 → Fe 2+ + SO42− 10 −4 10 −4 10 −4 →) Se calculan los números de transporte: NUMEROS DE TRANSPORTE 0 |Zi| λi ci |Zi| -2 3 2.04x10 -2 2 1.36x10 -2 2 1.60x10 -2 1 2.28x10 Especie 3+ Fe 2+ Fe 2SO4 Cl λi 68 68 80 76 ci -4 10 -4 10 -4 10 -4 3x10 Especie 3+ Fe 2+ Fe ti 0.280 0.187 n 3+ 2+ Fe +1e- º Fe 1 0 |Zi| 3 2 Σλj cj |Zj| -2 7.28x10 0 IM 8.87 8.88 Sale igual porque tienen iguales conductividades equivalentes a dilución infinita. ti 0.280 0.187 0.220 0.313 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS b) Además exista la disociación de KCl: KCl → K + i) + Cl − 0.1 →) 0.1 0.1 NUMEROS DE TRANSPORTE 0 |Zi| λi ci |Zi| -2 3 2.04x10 -2 2 1.36x10 -2 2 1.60x10 1 7.6 1 7.35 Especie 3+ Fe 2+ Fe 2SO4 Cl + K λi 68 68 80 76 73.5 ci -4 10 -4 10 -4 10 ≅0.1 0.1 Especie 3+ Fe 2+ Fe ti -3 1.36x10 -4 9.07x10 n 3+ 2+ Fe +1e- º Fe 1 0 |Zi| 3 2 Σλj cj |Zj| 15 0 ti -3 1.36x10 -4 9.07x10 -3 1.07x10 0.507 0.490 IM -2 4.31x10 -2 4.31x10 c) Si se supone que toda la corriente se debe a difusión se comete error en la determinación de hierro ya que existe una corriente de migración de Fe3+ hacia el polo negativo (cátodo en la electrolisis). Además Fe3+ difunde hacia el cátodo donde es reducido a Fe2+ en la electrólisis. Por tanto, la intensidad total es la suma de la intensidad debido a la difusión más la intensidad debido a la migración: ID = 95-8.87 = 86.13 µA IT = ID + IM ID = IT-IM Cuando se calcula concentración de Fe3+, al utilizar la Intensidad de corriente total en vez de exclusivamente la de difusión, el error que se comete es: %E = IT − I D I 8.87 *100 = M *100 = *100 = 10.3% ID ID 86.13 En el caso b, la corriente de migración se ve enormemente disminuida por la presencia de KCl como electrólito de fondo: ID = 95-0.0431 = 94.96 µA Cuando se calcula concentración de Fe3+, al utilizar la Intensidad de corriente total en vez de exclusivamente la de difusión, el error que se comete es: %E = IT − I D I 0.0431 *100 = M *100 = *100 = 4.5 x10 −2 % ID ID 94.96 Como se observa, al operar en presencia de electrólito soporte se minimiza la contribución del transporte de sustancia electroactiva por migración, con lo que se simplifica el tratamiento matemático de los sistemas electroquímicos, y además, se facilita la conductividad de la disolución al disminuir la resistencia de la célula electroquímica, Asimismo, puede colaborar a disminuir o eliminar algunos efectos debidos a la matriz. DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 4.- Se quiere determinar Fe2+ en disoluciones que contienen del orden de 10–3 M de dicho catión. Dichas disoluciones contienen, además, cloruros y sulfatos en concentración similar a la del hierro. El método de análisis se basa en la medida de corrientes límite de difusión. a) ¿Qué concentración de electrolito fondo (KCl) debe añadirse para que el error de los resultados sea inferior al 3 %? b) Si se obtuvieron corrientes del orden de 50 µA, utilizando un electrodo de platino de superficie eficaz 1.43 mm2. ¿Cuál será el espesor de la interfase si el coeficiente de difusión del Fe2+ es aproximadamente 2.8x10-5 cm2/s? Datos: Conductividades equivalentes: Fe2+ = 68; SO42– = 80 ; K+ = 73.5 ; Cl– = 76. -2 -4 Solución: [KCl]=1.31x10 M; δ=7.73x10 cm Como hemos visto en el ejercicio anterior: %E = IT − I D I %E *100 = M *100 ∴ I M = ID ID ID 100 IM = ± I T ti n Z Fe2+ difunde hacia el ánodo (polo positivo) para oxidarse a Fe3+ originando la corriente de difusión. Por otra parte Fe2+ migra hacia el cátodo (polo negativo) originando una corriente de migración, que se opone a la de difusión. La corriente total medida en el ánodo es la diferencia entre la corriente de difusión y la de migración. IT = ID-IM ID = IT-IM. Entonces: IM = I t n %E I t n t n % E ti n %E IT − T i ∴ i = 1 − ID ∴ T i = Z Z Z 100 Z 100 100 ti 3 ti 3x10 −2 −2 −2 = = 5.82 x10 −2 1 − ∴ 0.5ti = 3x10 − 1.5 x10 ti ∴ ti = −1 2 100 2 5.15 x10 Como ti = λ0i ci Z i n ∑λ c Z j =1 0 j j j 68 * 10 −3 * 2 ti = 68 * 10 −3 * 2 + 80 * 10 −3 * 2 + 73.5 * x + 76 * ( x + 10 −3 ) 0.0582 = 0.136 0.136 + 0.160 + 149.5 x + 0.076 x = 0.0131M DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS b) Hay que calcular el espesor de la interfase trabajando bajo la intensidad límite de difusión. Según la Ley de Fick: ID = KD(Cdisol-Celec); En condiciones límite, podemos suponer que Celec = 0, por tanto IT = ID = KD*Cdisol, siendo la constante de proporcionalidad: KD = nFSD0 d n = nº de electrones intercambiados (eq/mol) F = Cte de Faraday = 96500 co/eq S = superficie del electrodo (cm2) D0 = coeficiente de difusión de la especie (cm2/s) d = espesor de la interfase (cm) Por tanto: ID = nFSD0 nFSD0 Cdisol ∴ d = Cdisol d ID 1 * 96500 * 1.43 x10 −2 * 2.8 x10 −5 d= * 10 −3 * 10 −3 (cm 3 / L ) = 7.73 x10 −4 cm −6 50 x10 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 5.- Construir las curvas I-E de los siguientes ejemplos prácticos: c) Disolución de Fe2+ 0.1 M y de Fe3+ 0.05 M a pH=0 y a pH=2, con electrodo de Pt y calomelanos. d) Disolución de Fe2+ y Ce3+ 0.1 M en las condiciones anteriores. Datos: Eo (Fe3+/Fe2+) = + 0.77 V ; Eo (Ce4+/Ce3+) = + 1.0 V. a) Fe2+ 0.1 M Fe3+ 0.05 M pH = 0 y pH = 2 E0(Fe3+/Fe2+) = 0.7 v Formas oxidadas: Fe3+, H+ (H2O) Formas reducidas: Fe2+, O2- (H2O), H2 Fe3+ + 1e- º Fe2+ E0 = 0.77v 2H+ + 2e- º H2 E0 = 0.00v (reducción de H+ a H0) O2 + 4H+ + 4e- º 2H2O E0 = 1.23 v (reducción de O0 a O2-, médio ácido) En el ánodo ocurre la oxidación de Fe2+ a Fe3+ y, posteriormente, a potenciales mayores ocurrirá la oxidación del O2- procedente del H2O a O2 (vamos de potenciales más negativos a cada vez más positivos). En el cátodo ocurre la reducción del Fe3+ a Fe2+ y, posteriormente, la de H+ a H0 (vamos de potenciales más positivos a cada vez más negativos) Para estudiar las curvas se busca la relación I-E a partir de la ecuación de NERST y la Ley de FICK. E = E 0 + 0.059 Log [Ox]elec [Re d ]elec (En electrolisis, el ánodo es el polo positivo, la corriente de migración se opone a la de difusión) Según la Ley de Fick: IT = KFe2+([Fe2+]diso - [Fe2+]elec) Teniendo en cuenta que KFe2+[Fe2+]diso es la intensidad límite de difusión, IFe2+, cuando [Fe2+]elec = 0. IT = IFe2+ - KFe2+[Fe2+]elec [ Fe 2+ ]elec = I Fe − I K Fe 2+ 2+ El proceso de reducción consume electrones, es decir corriente eléctrica, por lo que su signo es negativo. Simplemente, se trata como si fuese oxidación, pero con el signo cambiado. DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS IT = - KFe3+([Fe3+]diso - [Fe3+]elec) Teniendo en cuenta que -KFe3+[Fe3+]diso es la intensidad límite de difusión, IFe3+, cuando [Fe3+]elec = 0. IT = IFe3+ + KFe3+[Fe+3]elec [ Fe 3+ ]elec = I T − I Fe K Fe 3+ 3+ Sustituyendo en la ecuación de Nerst: E = E 0 + 0.059 Log K Fe I − I Fe + 0.059 Log K Fe I Fe − I 2+ 3+ 3+ 2+ El potencial de semionda, E1/2, potencial cuando: I(E ) = 1 2 I Fe + I Fe 2 2+ 3+ E 1 = 0.77 + 0.059 Log 2 K Fe K Fe 2+ 3+ I Fe I − Fe 2 + 0.059 Log 2 I Fe I − Fe 2 2 2+ 3+ 2+ 3+ Suponiendo KFe2+ ≅KFe3+, queda que el potencial de semionda es igual al potencial normal. E 1 = E 0 = 0.77 2 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 0.11 0.10 0.09 0.08 0.07 0.06 0.05 Intensidad 0.04 0.03 0.02 0.01 0.00 -0.01 -0.02 -0.03 -0.04 -0.05 -0.06 0.60 0.70 0.80 Potencial 6.- Calcular la ecuación de la curva I-E, así como su potencial de semi-onda: a) Para una disolución de Cd2+ 10–3 M. b) Para una disolución de Cd2+ 10–3 M y NH3 1 M. Datos: ß4 (Cd(NH3)42+) = 106.56 , Eo (Cd2+/Cd0) = -0.402 V. E1/2= -0.4994 V; E1/2= -0.693 V 0.90 DEPARTAMENTO DE QUÍMICA ANALÍTICA Y TECNOLOGÍA DE ALIMENTOS 7.- Estudiar las curvas de I-E sobre un electrodo de mercurio en el transcurso de la valoración complexométrica de Cd2+ con EDTA. Siendo X ((Y4–)/(Cd2+)) = 0, 0.5, 1 y.2. Datos: Eo (Cd2+/Cd0) = -0.40 V; Eo (Hg2+/Hg0) = 0.86 V; Log Kd (CdY2-) = -16.1; Log Kd (HgY2-) = -20.4