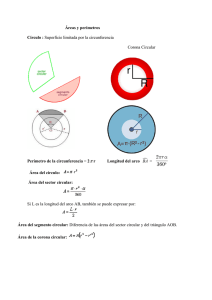
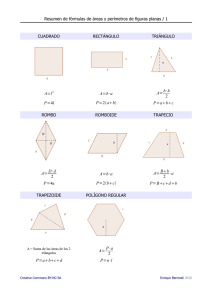
Geometría 1° de Secundaria: III Trimestre yanapa.com

Geometría 1° de Secundaria: III Trimestre
XI: ÁREA DE UN TRIÁNGULO
C
F
E
¿ AABC = b x h ?
2
h
A
B
b
Para realizar la demostración de la fórmula para hallar el área del triángulo haremos uso de
D
una construcción auxiliar: por el vértice C, trazaremos una paralela al segmento
AB
y por el
vértice B, trazaremos una línea paralela al segmento AC . El punto donde se cortan estas
dos líneas (punto de intersección) lo llamaremos E. Entonces se formará el cuadrilátero
ABEC. Asimismo, trazaremos las alturas
CD
y
FB , perpendiculares a los segmentos AB
y
CE , respectivamente.
El área del triángulo lo podremos hallar por una diferencia de áreas:
AABC = AABEC – ABCE … (1)
Ahora, si analizamos el cuadrilátero ABEC, notamos que, como todos sus lados son paralelos
dos a dos, entonces el cuadrilátero ABEC es un paralelogramo. En consecuencia, si la longitud
del segmento
AB
es “b”, por ser ABEC un paralelogramo, entonces la longitud del segmento
CE también es “b”.
Además, como sabemos que el área de un paralelogramo se obtiene multiplicando su base por
su altura, entonces:
AABEC = b x h … (2)
Ahora, si analizamos los triángulos ABC y BCE, observamos que como los segmentos
AB
y
CE tienen la misma longitud “b”, y las alturas CD y BF tienen la misma longitud “h”,
entonces los triángulos ABC y BCE son figuras equivalentes; y, como son figuras equivalentes,
por este motivo tendrán áreas iguales.
 AABC = ABCE … (3)
Si reemplazamos las ecuaciones (2) y (3) en la ecuación (1), obtendremos:
A ABC 
A ABEC  A BCE
 
A ABC

b x h  A ABC
Pasando AABC al lado izquierdo de la igualdad
AABC + AABC = b x h
2AABC = b x h
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Dividiendo cada término de la igualdad entre 2:
AABC = b x h
2
Área del Triángulo
Por lo que queda demostrada la fórmula para hallar el área del triángulo.
Esta fórmula del área del triángulo es aplicable a cualquier tipo de triángulo, el cual puede
ser:
a) Triángulo Escaleno.- Aquel que no tiene lados iguales, es decir, la longitud de sus lados es
diferente.
c
a
b
b) Triángulo Isósceles.-Tiene dos lados iguales, y al tercero se le considera como la base del
triángulo.
a
a
c)
b
Triángulo Equilátero.-Es aquel en el cual sus tres lados son iguales.
60º
60º
-
60º
El área del triángulo equilátero se puede hallar directamente si se conoce sólo la
longitud de su lado ó sólo la longitud de su altura, haciendo uso de las siguientes
fórmulas:
A= l
2
x
3
4
ó
h
2
A= h
x
3
3
yanapa.com
Geometría 1° de Secundaria: III Trimestre
-
La demostración la dejaremos pendiente, pues es necesario conocer nociones básica de
una rama de la Ciencia Matemática: la Trigonometría, curso que recién aprenderemos en
Tercero de Secundaria. Por este motivo, consideraremos como válidas “a priori” estas
dos fórmulas anteriores.
Conceptos Importantes
1. Teorema de Pitágoras Este teorema solamente se aplica a los triángulos rectángulos
(aquellos que poseen un ángulo de 90º). En un triángulo rectángulo los lados que se
interceptan en un ángulo de 90º se llaman CATETOS y al tercer lado se le conoce como
HIPOTENUSA.
Hipotenusa
h
C1
C2
Catetos
El teorema de Pitágoras se enuncia así: “La suma de los cuadrados de los catetos es igual
al cuadrado de la hipotenusa”.
Es decir:
C12  C22  h2
Teorema de Pitágoras
Si tenemos el siguiente triángulo rectángulo
h
3
4
La longitud de la hipotenusa la podremos hallar haciendo uso del Teorema de Pitágoras. En
efecto:
h2 
h2 
h2 
h 
C12  C 22
42  32
16  9  25
25
h  5
2. Semejanza de Triángulos (
)
Se dice que 2 triángulos son semejantes si cumplen con alguna de lo siguientes 3
criterios:
a)
Si al menos dos de sus 3 ángulos internos son iguales:
yanapa.com
Geometría 1° de Secundaria: III Trimestre
b
b)
a
c
d
a
c
Si dos lados del primer triángulo son proporcionales a dos lados del segundo, y los
ángulos formados por dichos lados son iguales.
Si:
a
m
b
n
c
a
p
m
c)
b
d
b
a
m
p
b
n
Si los tres lados del primer triángulo son proporcionales a los tres lados del
segundo.
Si:
c
a
3)
p
m
a
b
c
 
m n p
n
b
Congruencia de Triángulos (
) .-
Se dice que dos triángulos son CONGRUENTES (iguales), si cumplen con alguno de estos
3 criterios.
a)
Si tienen congruentes un lado y los ángulos adyacentes a él.
c
b
a
b=m
m
n
c=n
a
yanapa.com
Geometría 1° de Secundaria: III Trimestre
b)
Si tienen congruentes dos lados y el ángulo comprendido entre ellos.
a
c
a
m
b
c)
c=m
b
Si los tres lados de cada triángulo son congruentes entre ellos.
c
a
c
a
b
b
XII: ÁREA DE UN CUADRILÁTERO
Una vez conocidos estos teoremas importantísimos, estamos en condiciones de definir (y también
de demostrar) el área de las principales figuras geométricas. Empezaremos por los cuadriláteros.
Los cuadriláteros son figuras geométricas que poseen cuatro lados. Los cuadriláteros pueden ser:
* Rectángulo.
* Cuadrado
* Rombo
* Paralelogramo
* Trapecio
A continuación, pasaremos a detallar (y en algunos casos demostrar) el área de cada uno de estos
cuadriláteros.
1. Área del rectángulo
Un rectángulo es una figura geométrica que posee 4 lados paralelos dos a dos, e interceptados
bajo un ángulo de 90º. Los lados paralelos tienen igual longitud. El área de cualquier rectángulo
se obtiene multiplicando la longitud de su base por la longitud de su altura.
A RECTÁNGULO = B X h
H
B
Demostración: ¿AABCD = h x b?
C
B
h
A
A
b
N
P
H
A1
M
B
Q
D
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Para realizar la demostración de que el área del rectángulo ABCD es A = h x b, haremos una
construcción auxiliar: dibujaremos un rectángulo MNPQ de altura “H” y base “B”, donde H = B = 1;
es decir, tenemos un rectángulo de lado unitario. Este rectángulo será la unidad de área, es decir A1
= 1. (Nótese que como la base y altura son iguales, este rectángulo recibe el nombre de “cuadrado”).
Sabemos, por el Cuarto Teorema, que las áreas de 2 rectángulos son proporcionales al producto de
su base por su altura respectiva. Entonces:
A
h x b …. (1)

A1
HxB
Pero sabemos que A1 es uno, y que H = B = 1.
Entonces reemplazando estos valores en la ecuación (1).
A  h x b : Área del rectángulo
Por lo que queda demostrada la fórmula para hallar el área del rectángulo.
2. Área del Cuadrado
Un cuadrado es un tipo particular de rectángulo, donde la longitud del la base es igual a la
longitud de la altura. El área del cuadrado se obtiene elevando al cuadrado la longitud de la
base, o elevando al cuadrado la longitud de la altura. Es decir, multiplicando h x h ó b x b.
D
L
L
Demostración:
Puesto que conocemos que el área del rectángulo es:
A=hxb
Y como hemos dicho, en un cuadrado: h = b = L

A  L x L  L2
Área del Cuadrado
Obs.
El área del cuadrado también puede obtenerse así:
Donde D es la diagonal del cuadrado
3.
A
D2
2
Área del Paralelogramo
Un paralelogramo es una figura de 4 lados, donde sus lados son paralelos dos a dos, pero donde
el ángulo de intersección de los lados es distinto a 90º.
El área de un paralelogramo se obtiene multiplicando la longitud de su base por la longitud de su
altura; es decir, igual que el área del rectángulo, puesto que el paralelogramo es un tipo de
rectángulo al cual se le han inclinado dos lados.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Demostración:
B
A ABCD  b x h
C
h
A
F
D
b
Primero, debemos notar que tanto los segmentos AD y BC tienen la misma longitud, así como
E
los segmentos AB y CD. Para demostrar que el área del paralelogramo es
A = b x h haremos
una construcción auxiliar: prolongaremos el segmento AB y trazaremos las perpendiculares
CF y BE . Entonces se formarán los triángulos rectángulos ABE y CDF y el cuadrilátero EBCF.
Ahora, hallaremos el área del paralelogramo ABCD mediante el uso de suma y diferencia de
áreas.
Entonces: AABCD = AEBCF + AABE – ACDF …(1)
Ahora, analicemos el cuadrilátero EBCF: observamos que los segmentos EB y CF son paralelos
y sabíamos que los segmentos BC y AD eran paralelos, y como el ángulo de intersección de los
lados es 90º, entonces el cuadrilátero EBCF es un rectángulo.
Entonces: AEBCF = BC x EB = b x h … (2)
Ahora, analicemos los triángulos rectángulos ABE y CDF: como los segmentos AB y CD
son iguales y los ángulos interiores de los triángulos son iguales, entonces los dos triángulos son
idénticos, (figuras equivalentes), por lo que tendrán la misma área.
Entonces: AABE = ACDF … (3)
Si reemplazamos las ecuaciones (2) y (3) en la ecuación (1), obtendremos:
A ABCD  A EBCF  A ABE  A CDF


Área
del
A ABCD 



b x h  A ABE  A ABE
A ABCD  b x h
Paralelogramo
Por lo que queda demostrada la fórmula para hallar el área del paralelogramo.
a.
b.
c.
Un triángulo rectángulo es aquel que tiene un ángulo de 90º como ángulo interior.
Se dice que dos rectas o segmentos que pertenecen a un mismo plano son PARALELOS si,
por más que extendamos dichas rectas o segmentos, estas dos nunca, se cortarán. Un
ejemplo de rectas paralelas son las líneas horizontales de un cuaderno cuadriculado.
Se dice que dos rectas o segmentos
que pertenecen a un mismo plano son
PERPENDICULARES si dichas rectas o segmentos se cortan en un ángulo de 90º. Un
ejemplo de rectas o segmentos se cortan en un ángulo de 90º. Un ejemplo de rectas
perpendiculares sería el cruce de una línea horizontal de un cuaderno cuadriculado con una
línea vertical del mismo,
yanapa.com
Geometría 1° de Secundaria: III Trimestre
d.
4.
Cada vez que hablemos de la altura se considerará que la altura es perpendicular a la base
de la figura analizada.
Área del Rombo:
Un rombo es una forma particular del paralelogramo, en donde las diagonales de éste
paralelogramo se cortan perpendicularmente (en un ángulo de 90º).
El área de un rombo se obtiene multiplicando las longitudes de sus diagonales y dividiendo el
resultado entre dos. Es decir:
N
Si la diagonal MP es “d” y
la diagonal NQ es “D”
A1
A3
P
A4
A
A2
= Dxd
2
D
Q
5.
Entonces
d
M
A1 = A2 = A3 = A4 si el rombo es simétrico
Área del Trapecio
Un trapecio es un cuadrilátero que posee dos lados paralelos conocidos como base mayor (el lado más
grande) y base menor (el lado más pequeño) y dos lados no paralelos.
El área de un trapecio se obtiene sumando la base mayor con la base menor dividiendo el
resultado entre dos y, finalmente, multiplicando este resultado por la longitud de la altura del
trapecio.
b
A TRAPECIO = b + B
2
2
bm
x
H
Donde:
b : base menor
B : base mayor
bm : base media
H : altura
2
B
A esta semisuma (suma dividida entre 2) de la base mayor y la base menor se le conoce como
BASE MEDIA. La base media viene a ser un segmento que se encuentra a la misma distancia de
la base mayor y la base menor (H/2); es decir se encuentra en el “medio” de las 2 bases,
además es paralela a ellas.
bm 
bB
2
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Por lo que el área del trapecio también se puede formular así:
ATRAPECIO = bm x H
.
XIII: ÁREA DE SUPERFICIES CIRCULARES
A continuación detallaremos como obtener el área de superficies circulares. La base es el
área del círculo, así que apréndete bien la fórmula para su área y las demás te serán fáciles.
1. Área del Círculo
Un círculo es una figura geométrica que tiene la particularidad de que la distancia que
existe entre su centro (0) y sus extremos es siempre constante; a dicha distancia se le
conoce con el nombre de RADIO (r).
r
Figura I
B
r
r
O
A
Observaciones
a) Hay que tener cuidado de no confundir círculo con circunferencia. La circunferencia es
la línea que delimita el área circular, es decir, el borde del círculo; en cambio, el círculo
abarca la circunferencia y todo el espacio (área) que ésta encierra.
b)
Cuando dos radios forman parte de una misma recta, es decir son colineales (como en el
caso de los radios OA y OB ), al segmento que va desde un extremo a otro de la
circunferencia pasando por su centro (segmento AB ) se le denomina DIÁMETRO (D).
 D = 2r
c)
La longitud de la circunferencia (L) se puede obtener así:
L = 2r ó L = D
El área de un círculo es proporcional al cuadrado del radio del círculo. La constante de
proporcionalidad es un número irracional que recibe la notación de la letra griega (pi).
 = 3.1415927… 
  3.14
Es decir, el área de un círculo se puede calcular así:
A  r 2
 Área del Círculo
La demostración de ésta fórmula la dejaremos pendiente, pues es necesario conocer
conceptos de Matemática Superior, específicamente en el campo de Límites de funciones,
yanapa.com
Geometría 1° de Secundaria: III Trimestre
tema que (generalmente) se aborda en cursos de Álgebra Universitaria. Por este motivo,
consideraremos como válida “a priori” esta fórmula.
9. Área de una Corona Circular
Una corona circular es una superficie delimitada por las circunferencias de dos círculos
concéntricos (dos círculos son concéntricos si tienen el mismo centro).
Corona Circular
r
R
El área de una corona circular se obtiene multiplicando por  a la diferencia de los
cuadrados de los radios de cada círculo. Es decir:
A 
x
R2  r2
r
Figura II
R
A
Demostración:
Sea la corona circular de la figura II, cuyas longitudes de sus radios son r y R para el círculo
menor y círculo mayor respectivamente.
Consideraremos que el área del círculo de radio “r” es A1 y el área del círculo del radio “R” es
A2.
Entonces, podemos representar el área de la corona circular (A) de la siguiente manera:
A = A2 – A1 … (1)
Pero, como sabemos que el área de un círculo es igual a  por el radio elevado al cuadrado, el
área del círculo de radio “r” lo podemos expresar así:
A1 =  x r2 … (2)
Y el área del círculo de radio “R” lo podemos expresar así:
yanapa.com
Geometría 1° de Secundaria: III Trimestre
A2 =  x R2 … (2)
Ahora, reemplazando las ecuaciones (2) y (3) en la ecuación (1) obtenemos:
A  A 2  A1


A   x R2   x r 2
Factorizando  de cada sumando, obtenemos:

A   x R2  r 2

Área de una corona circular
Por lo que queda demostrada la fórmula para obtener el área de una corona circular.
10. Área de un Sector Circular:
Un sector circular es una porción del círculo, que tiene la particularidad de estar limitado
por 2 radios y por la circunferencia asociada al círculo.
El área de un sector circular se obtiene multiplicando la longitud del arco asociado al sector circular
por el radio del círculo y dividiendo éste resultado entre dos.
NOTA: El arco de un sector circular viene a ser la porción de la circunferencia que limita al
sector circular. La longitud del arco de un sector circular se denota por “l” y es
igual a:
 
.r .
180º
Donde  es la medida del ángulo que forman los 2 radios que delimitan al sector universal.
La medida del ángulo  debe darse en grados sexagesimales, los cuales se pueden obtener
empleando cualquier transportador.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Demostración:
P
r
O
A
r
¿ APOQ = b x r ?
2
Q
Lo primero que debemos saber, previo a la demostración de ésta fórmula, es que un círculo
completo tiene 360º (¡Compruébalo con tu transportador”).
Ahora, sabemos que el área de un círculo se obtienen así: A = r2 y que este círculo barre un
ángulo de 360º. Si usamos una Regla de Tres Simple podremos hallar el área de un sector
circular de “” grados puesto que consideraremos al círculo como un sector circular de 360º
ÁNGULO
ÁREA
Si:
360º
r2
Si:

A= ??
 A=
 x x r 2
360º
… (I)
Si arreglamos este resultado convenientemente, obtendremos:
A 

Pero:
xr x Xr
... ( 1 )
180º x 2
xr x
… (2)
180º
Entonces, reemplazando la ecuación (2) en la ecuación (1), obtendremos:
A 
l
x
2
r
Área de un Sector Circular
OBSERVACIONES:
a. A pesar de que la anterior fórmula es la presentación formal de cómo hallar el área del
sector circular, podemos hacer uso directamente de la fórmula (I), ya que es más
directa.
b. Al sector circular también se le llama SECCIÓN CIRCULAR, por ser una parte del círculo.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
c.
El área de un sector circular es equivalente a la de un triángulo que tenga por base la
longitud del arco que limita al sector y que tenga por altura la longitud del radio de la
circunferencia.
En efecto:
O
O
r
r
r
r
A
B

A SECTOR
CIRCULAR
B
A
l xr
l xr
 A TRIÁNGULO 
2
2
Esto se debe a que el sector circular es una clase particular de triángulo, llamado
TRIÁNGULO MIXTILÍNEO, el cual está formado de líneas rectas y líneas curvas.
11. ÁREA DE UN TRAPECIO CIRCULAR
Un trapecio circular viene a ser una sección (porción) de una corona circular.
El área de un trapecio circular limitado por 2 arcos y por radios diferentes de dos
círculos se puede calcular mediante la siguiente fórmula:
A 
  R2  r 2
360 º
Trapecio Circular
Demostración:
¿A
R

x

R2  r2
360º
x
?
MN=
M
P

A
L
N
Q
PQ
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Consideremos que en el anterior gráfico el área del trapecio circular MNPQ es “A”. El
círculo mayor tendrá un radio de longitud “R” y la longitud de su arco PQ será “L”. El
círculo menor tendrá un radio de longitud “r” y la longitud de su arco MN será “l”. El
ángulo entre los radios
OP
y
OQ
será “”.
El área del trapecio circular se puede expresar como la diferencia del área del sector
circular OPQ menos el área del sector circular OMN.
Entonces:
AMNPQ = AOPQ – AOMN … (1)
Pero sabemos que el área de un sector circular es

AOPQ =
LxR
2

AOMN =
l xr
2
l xr
2
Pero, usando el concepto de longitud de arco, tenemos:

AOPQ =
 AOPQ =

 x  x R

x R
 180º 
2
 x  x R2
… (2)
360º
 x  x r

xr
 180º 
AOMN =
2
 AOMN =
 x  x r2
2
…(3)
Esto se debe a que el ángulo para las dos secciones circulares es el mismo y es igual a “”.
Ahora, reemplazando las ecuaciones (2) y (3) en la ecuación (1), obtenemos:
yanapa.com
Geometría 1° de Secundaria: III Trimestre
A MNPQ  A OPQ  A OMN






A MNPQ 
Factorizando
 x  x R2  x  x r 2

360º
360º
  x 

 de cada sumando, obtenemos:
 360º 
A MNPQ 

 x  x R2  r 2
360º

Área del Trapecio Circular
Por lo que queda demostrada la fórmula para hallar el área de un trapecio circular.
Observaciones:
a. La demostración de ésta fórmula también podría obtenerse mediante una regla de tres simple,
haciendo una comparación entre el área de una corona circular (asociada a un ángulo de 360º) y el
área de un trapecio circular (asociado a un ángulo ).
b.
El área de un trapecio circular es equivalente a la de un trapecio rectilíneo que tenga por
bases a los arcos rectificados que limitan al trapecio circular y por altura la diferencia
de los radios.
En efecto:
O
D
C
r
R
R-r
D
C
R-r
A
A
B
B
L
L
yanapa.com
Geometría 1° de Secundaria: III Trimestre
A TRAPECIO 
CIRCULAR
A TRAPECIO 
CIRCULAR
A TRAPECIO 
CIRCULAR
Pero:


 x  x R2  r 2
360º

 x  x  R  r R  r 
360º
1  x  x R  x  x r 

x R  r 
2  180º
180º 
xRx
xxR
L y
l
180º
180º
A TRAPECIO 
CIRCULAR
1
 L  l  x R  r   A TRAPECIO
2
12. Área del Segmento Circular
Un segmento circular es una porción de un sector circular que se encuentra delimitada
por el arco de la circunferencia asociado al sector circular y el segmento que une las
intersecciones de los radios con la circunferencia.
Segmento Circular
A
B
El área de un segmento circular se obtiene mediante la diferencia del área del sector
AOB con el área del triángulo AOB.
ÁREA DEL SEGMENTO CIRCULAR
A  A SECTOR
CIRCULARAOB
 A TRIÁNGULOAOB
yanapa.com
Geometría 1° de Secundaria: III Trimestre
CUADRO RESUMEN: ÁREAS DE POLÍGONOS
FIGURA
ÁREA
h
Rectángulo
A = b x h
b
D
a
Cuadrado
D2
2
A = a2 ó A =
a
Triángulo
bxh
2
A =
h
b
Paralelogramo
h
A = h x b
b
b
Trapecio
B  b
A  
xh
 2 
h
B
Rombo
d
r
Círculo
Corona Circular
A = (R2 – r2)
r
A =
r
r
Trapecio Circular
A =
R
A
Dxd
2
A = r2
R r
Sector Circular
Segmento Circular
A 
D
B
 x r2 x 
360º

 x  x R2  r 2
360º
A  A SECTOR
CIRCULAR

 A TRIÁNGULOAOB
yanapa.com
Geometría 1° de Secundaria: III Trimestre
T
XIV: OPERACIONES CON ÁREAS
I. Suma de Áreas, Diferencia de Áreas:
Si tenemos el siguiente trapecio:
D
C
A2
A1
B
A
1.
Para hallar el área A del trapecio, la podremos obtener SUMANDO el área A1 y el área A2, es
decir sumando las respectivas áreas de los triángulos ADC y ABC. Por lo tanto:
Área del
Trapecio
2.
A = A1+ A2
Igualmente, si quisiéramos obtener el área del triángulo ABC, la podríamos hallar RESTANDO el
área del trapecio ABCD menos el área del triángulo ADC. Por lo tanto:
Área del
Triángulo ABC
-
A1 = A - A 2
El área de una superficie geométrica se denota con una letra “a” mayúscula. Sin embargo,
en varios libros el área de una superficie geométrica se denota con una letra “S”
mayúscula. Si bien estas notaciones se pueden usar indistintamente, nosotros usaremos
la primera de éstas  Área = A.
II. Figuras Equivalentes
Son aquellas que son iguales o pueden obtenerse como suma o diferencia de figuras iguales.
Todas las figuras equivalentes tienen IGUAL ÁREA.
Del mismo modo, si dos figuras geométricas tienen igual área, se dice que son figuras
equivalentes.
Es decir, dadas las siguientes figuras:
B
C
A2
A1
A
P
N
D
M
Q
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Donde:
A1 es el área del cuadrado ABCD y A 2 es el área del paralelogramo MNPQ, si A1 =
A2 entonces las dos son figuras equivalentes.
Las figuras equivalentes tienen algunas características:
1. Identicidad
A es equivalente a A.
2. Reciprocidad
Si A1 es equivalente a A2, entonces A2 es equivalente a A1.
3. Transitividad
Si A1 es equivalente a A2 y
A2 es equivalente a A3
Entonces A1 es equivalente a A3
*
Estas características las podremos notar mejor en el desarrollo del tema.
*
Antes de presentar las fórmulas para hallar el área de las principales figuras
geométricas, con sus respectivas demostraciones, enunciaremos algunos teoremas
imprescindibles, con el objeto de entender de una manera óptima las posteriores
demostraciones.
A. Primer Teorema
“Si dos rectángulos tienen igual base e igual altura, entonces los dos rectángulos son iguales”
B
C
Altura (h): 3
A
Q
P
h=3
4
D
S
b=4
R
Base (b)
Como tanto la base como la altura de los rectángulos ABCD y PQRS son las mismas,
entonces los rectángulos son iguales.
B. Segundo Teorema
“Si dos rectángulos tienen iguales las bases, sus áreas son proporcionales a las alturas
de cada uno de ellos”
yanapa.com
Geometría 1° de Secundaria: III Trimestre
C
B
P
N
5
A1
A
4
D
3
A2
M
4
Q
Como los dos rectángulos tienen igual base (b= 4), entonces sus áreas son D.P. a sus alturas.

A1

AB
A2

MN
A1
5

A2
3
C. Tercer Teorema:
“Si dos rectángulos tienen las alturas iguales, sus áreas son proporcionales a las bases”.
D. Cuarto Teorema:
“Las áreas de dos rectángulos son proporcionales a los productos de sus bases por sus
alturas”
C
B
P
N
Demostración:
h
A1
A
b
¿
A1
A2
D

H
A2
M
B
Q
T
S
H
A3
R
b
U
bxh
?
BxH
Haremos primero una construcción auxiliar y formaremos un rectángulo RSTU con base “b” (igual a la
del rectángulo ABCD) y con altura “H” (igual que la del rectángulo MNPQ).
Sabemos, por el Segundo Teorema, que como los rectángulos ABCD y RSTU tienen la misma
base (“b”), entonces sus áreas serán proporcionales a sus alturas.
Entonces:
A1
h

A3
H
yanapa.com
Geometría 1° de Secundaria: III Trimestre
 A3 
H
A 1 … (1)
h
Además, por el Tercer Teorema, sabemos que como los rectángulos MNPQ y RSTU tienen la misma
altura (“H”), entonces sus áreas son proporcionales a sus bases. Entonces:
A2
B
 A3 

A3
b
b
A 2 … (2)
B
Al observar las ecuaciones (2) y (3), notamos que estas ecuaciones son iguales, ya que indican
a qué es igual el área A3.
Por lo tanto:
A3 

H
b
A1  A 2
h
B
A1 b x h

A2 H x B
Por lo que queda demostrado el Cuarto Teorema

Relaciones Importantes entre Áreas:
I.
Triángulos
a.
A1
b1
A2
A1
b1
A2
b2
b2
yanapa.com
Geometría 1° de Secundaria: III Trimestre
b.
A1
A2
A2
H
h
h
H
A1
II. Paralelogramos
c.
A1 = A2 = A3 = A 4 = A
4
A2
A1
A3
Donde A es el área del paralelogramo
A4
d.
B
P
C
A1
A 1 = A ABCD
2
Donde P es cualquier punto entre B y C
A
D
e.
B
C
A 1 + A 2 = A ABCD
2
A1
A
III.
P
A2
D
Trapecios:
f.
C
B
A1 = AABCD
2
A1
A
D
yanapa.com
Geometría 1° de Secundaria: III Trimestre
g.
A1 = A 2
A3
A1
A2
A1 . A 2 = A 3 . A 4
2
A4
A ABCD = A3 + A 4
h.
B
C
A 1 = A2 = A3 = A
A1
3
A2
A3
A
D
- Las unidades de las áreas son metro cuadrado (m2), centímetro cuadrado (cm2), etc.
XV: RECTA Y PLANO
I. Planos: Determinación, posiciones relativas de dos planos. Posiciones relativas de un
plano con una recta. Teoremas. Distancias
1. Determinación de Planos
Un plano viene determinado:
a) Por dos rectas que se cortan.
b) Por 3 puntos no situadas en línea recta (no colineales).
c) Por una recta y un punto exterior a ella.
d) Por 2 rectas paralelas.
2.
Posiciones Relativas de dos planos
Dos planos pueden ocupar las siguientes posiciones:
a)
Cortándose:
En este caso tienen una recta común que se llama “intersección de los dos planos”.
b)
Ser Paralelos:
Cuando no tienen ningún punto en común.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
1
2
1
2
Paralelos
Cortándose
3.
Posiciones Relativas de un Plano con una recta
Una recta y un plano pueden ocupar las siguientes posiciones:
a) Estar la recta en el plano.
b) Cortándose. En este caso tienen un punto A en común.
c) Ser paralelas. En este caso no tienen algún punto en común.
4.
Posiciones Relativas de dos rectas en el espacio
Dos rectas en el espacio pueden ocupar las siguientes posiciones:
a) Cortándose. En este caso tienen un punto en común.
b) Ser paralelas. En este caso están en un mismo plano y no tienen algún punto en común.
c) Cruzándose. En este caso no están en un mismo plano y no tienen ningún punto en común.
También se les llama RECTAS ALABEADAS.
Teoremas Importantes
a) “Las intersecciones a y b de dos planos paralelos  y  con un tercer plano  son rectas
paralelas”.
5.
a
b
b)
“Si dos rectas a y b son paralelas, todo plano  que pase por una de las dos rectas es
paralelo a la otra recta”.
a
b
c)
“Si un plano  corta a una de 2 rectas a y b paralelas corta también a la otra”.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
b
a
d)
“Si una recta corta a uno de dos planos paralelos, corta también al otro”.
e)
“Si se cortan dos rectas por un sistema de planos paralelos entonces, los segmentos
correspondientes son proporcionales”.
Imagen I
C
N
D
Entonces:
=
A
M
B
f)
“Si una recta es perpendicular a un plano , cualquier plano  (y todos los planos paralelos
a ) que pase por la recta es perpendicular a ”

Distancia entre 2 puntos
Viene a ser la longitud del segmento que une dichos puntos.
6.
Recta Perpendicular a un Plano
Se dice que una recta es perpendicular a un plano si es perpendicular a todas las rectas del plano
que pasan por la intersección. Al punto de intersección se le llama Pie de la perpendicular (punto
P).
P
7.
Distancia de un punto P a un plano :
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Es el segmento PM de perpendicular trazada del punto al plano; se llama así por ser MENOR que
cualquier otro segmento PN que une el punto con cualquier otro punto del plano.
P
M
N
8.
Paralelismo y Perpendicularidad
* Si de dos rectas paralelas a y b, una de ellas (a) es perpendicular a un plano, la otra (b)
también es perpendicular al plano.
* Recíprocamente, dos rectas perpendiculares a un mismo plano son paralelas.
* Dados dos planos paralelos, si una recta es perpendicular a uno de ellos, entonces
también es perpendicular al otro.
9.
Distancia entre dos plano  y  paralelos
Es el segmento MN perpendicular comprendido entre los 2 planos. O también, es la distancia
de un punto cualquiera M de uno de ellos al otro.
10. Proyección de un punto A sobre un plano 
La proyección de un punto A sobre un plano es el pie A’ de la perpendicular trazada desde el
punto al plano.
A
A’
La proyección de una línea AB sobre un plano  es el conjunto
proyecciones de todos los puntos de la línea.
A' B'
formado por las
yanapa.com
Geometría 1° de Secundaria: III Trimestre
A
B
A’
B’
11. Distancia entre dos rectas que se cruzan
Es el segmento perpendicular común comprendido entre ambas rectas. Para trazar esta
distancia, sean a y b las dos rectas alabeadas. Por un punto M de una de ellas (b) se traza la
recta c paralela a la otra (a), la cual determina con b el plano . Se traza ahora al plano ,
perpendicular al plano , el cual corta a la recta a en el punto P. Trazando desde P la
perpendicular
b.
PQ
al plano , tenemos que
PQ
es la distancia buscada entre las rectas a y
a
P
b
*
M
Q
c
Para desarrollar este capítulo de una manera óptima es necesario recordar el Teorema de
Pitágoras:
c
b
c2 = a2 + b2
a
Esto nos ayudará mucho en el momento de hallar distancias.
XVI: ÁREA DE SÓLIDOS
a) Tetraedro
Llamado así porque posee 4 caras. Se obtiene uniendo en el espacio 4 triángulos equiláteros iguales.
D
D
A
B
A
D´´
C
D´
Desarrollo del Tetraedro
B
C
Tetraedro
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Como los 4 triángulos equiláteros son iguales, entonces:
Atetraedro = 4 Atriáng.equiláteros
 h2 3 

 3 


l2 3

 4 


= 4
=4

b)
A tetraedro  l 2 3
ó
A tetraedro 
4
3 h2
3
Hexaedro (Cubo)
Llamado así porque posee 6 caras. Se obtiene uniendo en el espacio 6 cuadrados iguales.
E
F
D
C
D
C
E
E´´
F´
E´
F
L
H´´
A
B
H
G
G´
A
H´
H
Desarrollo del Cubo
B
L
G
L
Hexaedro o Cubo
Como los 6 cuadrados son iguales:
Acubo = 6 Acuadrado
 Acubo = 6L2
c)
.
Octaedro
Llamado así porque posee 8 caras. Está formado por 8 triángulos equiláteros iguales, que
se unen de 4 en 4 formando una pirámide de base cuadrada y finalmente uniendo las
bases de ambas pirámides.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
A
D
E
C
A
B
A
E
B
B
D
C
B
P
R
P
P
N
D
N
C
Q
P
Q
Q
R
N
Desarrollo del Octaedro
Acoplamiento de Pirámides
Octaedro
Como los 8 triángulos equiláteros son iguales, entonces:
A octaedro  2l 2 3
d)
ó
A octaedro 
8
3 h2
3
Paralelepípedo
Está formado por 6 paralelogramos: 4iguales entre sí y 2 iguales entre sí:
Desarrollo del Paralelepípedo
Paralelepípedo
Su área se obtiene sumando las áreas de cada paralelogramo.
Una forma especial de paralelepípedo es el ortoedro, el cual tiene la particularidad de
que está formando por rectángulos.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
Ortoedro
Desarrollo del Ortoedro
Análogamente, su área se obtiene sumando las áreas de cada rectángulo.
e)
Cilindro Recto
Está formando por 2 círculos idénticos que se encuentran en planos paralelos, revestidos
por una superficie convexa de forma rectangular.
r
r
r
2 r
H
H
r
Desarrollo del Cilindro Recto
Cilindro Recto
Su área se obtiene sumando las áreas de los círculos y el rectángulo.
 Acilindro = 2r2 + 2r(H)
f)
Cono
Formando por un círculo y una sección circular:
yanapa.com
Geometría 1° de Secundaria: III Trimestre
r
g
g
g
H
AB = 2 r
A
B
Arco AB
Desarrollo del Cono
r
Cono
g 2 = H2 + r2 .
Por Pitágoras:
g = generatriz
h = altura del cono
r = radio
Su área se obtiene sumando las áreas del círculo y del sector circular.
XVII: VOLÚMEN DE SÓLIDOS
Teorema Fundamental
“El volumen de un poliedro se obtiene multiplicando el área de su base por la altura del
poliedro”.
La unidad del volumen de un poliedro es el metro cúbico (m3).
Así:
VSÓLIDO  ABASE X ALTURA
H
r
Base
Volumen de los Principales Sólidos
a)
Volumen de un Tetraedro Regular:
yanapa.com
Geometría 1° de Secundaria: III Trimestre
V
a
a
H
VTetraedro  A ABC x H
C
a
b)
B
a
Volumen del Cubo (Hexaedro)
VCUBO  a 3
c)
Volumen de un Octaedro Regular:
D
A
C
h
3
B
a
d)
VOctaedro  2A ABCD x
a
h
a
Volumen de un Paralelepípedo
c
H
h
a
b
V  APARALELOGR AMO X H
Ortoedro
V  axbxc
yanapa.com
Geometría 1° de Secundaria: III Trimestre
e)
Volumen de un Cilindro Recto:
O R
G
G
H
O´
f)
G: Generatriz; en este caso G = H
VCilindro  ACírculo x H
VCilindro 
R
xR
2
xH
Volumen de una Pirámide
Una pirámide es un sólido muy especial. Su base puede ser cualquier polígono y todas sus
caras (excepto la base) se unen en un solo vértice, llamado CÚSPIDE.
Su volumen se obtiene multiplicando el área de la base por la tercera parte de su altura.
V
Cúspide
V  A BASE
a
x
H
3
H
a
Base
a
Si observas cuidadosamente al octaedro, te darás cuenta que está formado por 2 pirámides
de base cuadrada, motivo por el cual, en el cálculo de su volumen, su altura se encuentra
dividida entre 3. Esta división de la altura es una particularidad de los sólidos de forma
triangular.
g)
Volumen del Cono
Como un cono también tiene forma triangular, para calcular su volumen dividiremos su altura
entre 3.
yanapa.com
Geometría 1° de Secundaria: III Trimestre
V
VCono 
g
h
 x r2 x h
3
g
g: Generatriz del Cono
r
Como se observa, el volumen del cono resulta siendo la tercera parte del volumen del cilindro.
Prisma y Tronco de Prisma:
Llamaremos PRISMA, al sólido limitado por la superficie prismática cerrada y 2 planos
paralelos y secantes a dicha superficie. En este curso sólo nos interesaremos de los prismas
RECTOS, es decir, aquellos cuyas caras laterales son rectángulos.
F
D
E
V  AABC x h
h
ABC - DEF
es un prisma
N
M
A
C
B
Se llama TRONCO DE PRISMA al sólido determinado al cortar un prisma mediante un plano
NO paralelo a sus bases. Del gráfico anterior, ABC-DMN es un tronco de prisma.
Casos de Troncos de Prismas:
i)
ii)
a
b
c
 abc 
V  ABASE x 

3


a
c
 ab
V  ABASE x 

 3 
iii)
a
a
V  ABASE x  
3
yanapa.com