Tema 8 Integral definida

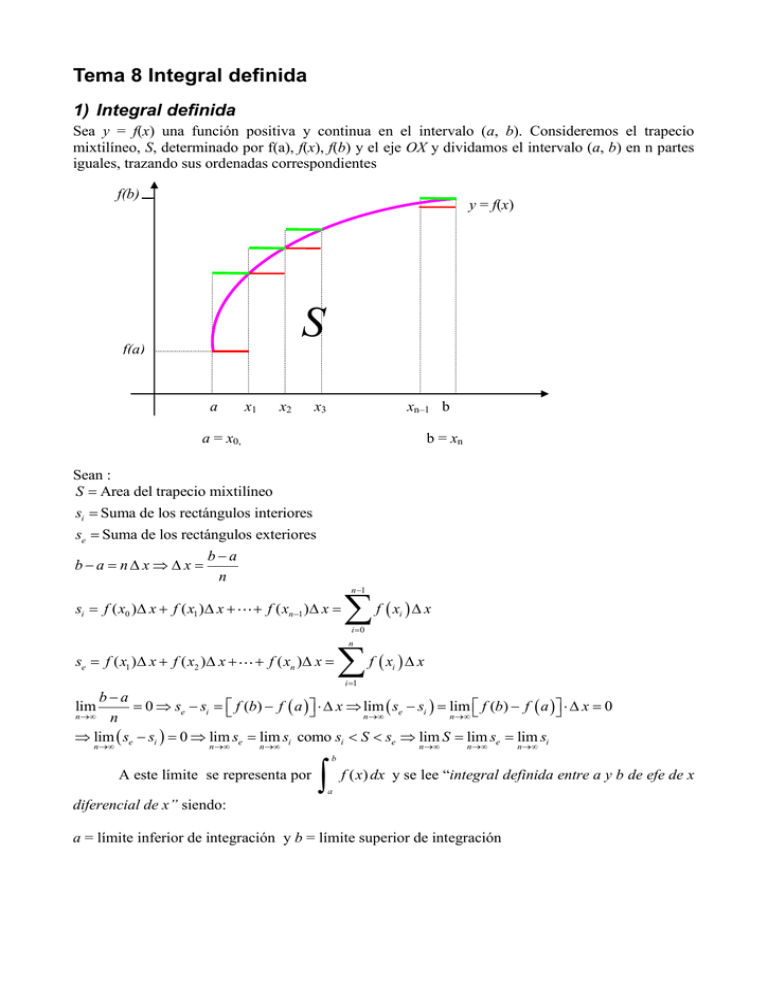
Tema 8 Integral definida
1) Integral definida
Sea y = f(x) una función positiva y continua en el intervalo (a, b). Consideremos el trapecio
mixtilíneo, S, determinado por f(a), f(x), f(b) y el eje OX y dividamos el intervalo (a, b) en n partes
iguales, trazando sus ordenadas correspondientes
f(b)
y = f(x)
S
f(a)
a
x1
x2
x3
xn–1 b
a = x0,
b = xn
Sean :
S  Area del trapecio mixtilíneo
si  Suma de los rectángulos interiores
se  Suma de los rectángulos exteriores
ba  n x   x 
ba
n
n 1
si  f ( x0 ) x  f ( x1 ) x 
 f x  x
 f ( x ) x 
 f x  x
 f ( xn 1 ) x 
i
i 0
n
se  f ( x1 ) x  f ( x2 ) x 
n
i
i 1
ba
lim
 0  se  si   f (b)  f  a     x  lim  se  si   lim  f (b)  f  a    x  0
n 
n 
n 
n
 lim  se  si   0  lim se  lim si como si  S  se  lim S  lim se  lim si
n 
n 
n 
A este límite se representa por
n 

n 
n 
b
f ( x) dx y se lee “integral definida entre a y b de efe de x
a
diferencial de x” siendo:
a = límite inferior de integración y b = límite superior de integración
2) Relación entre la integral definida e indefinida
En el trapecio mixtilíneo hacemos fija la abscisa inicial
variable la abscisa final mediante x. de este
es una función de x y la llamamos S(x)
Área rectángulo interior = f(x) x
a
y
modo, el área
Área rectángulo superior = f(x) (x + x),
entonces: f(x) x <
S
S(x) < f(x) x
Dividiendo por x:
a
f ( x) 

x
x + x
 S  x
 S  x
 f  x   x   lim
 f  x   d S  x   f  x  dx 
x 0
x
x
 d S  x   f  x  dx  S  x    f  x  dx
Por tanto, el área es una función primitiva de f(x)
3) Regla de Barrow. Valor de la integral definida
Sea  f ( x) dx  F ( x)  C
En el trapecio mixtilíneo hacemos fija la a y variable la b mediante x.
b
Sea S ( x)   f ( x) dx  F ( x)  C
a
a
Si x = a, el área vale cero. S (a)   f ( x) dx  F (a)  C  0  C   F (a)
a
sustituyo
el
valor
de
a
x
 S ( x)   f (t ) dt  F ( x)  F (a) haciendo
a
x
=
b.
S (b)   f ( x) dx  F (b)  F (a)   F ( x) a
b
b
a
Ejemplo:
3
 x2

 22
 9
32
7
x

1
dx


x


3

  2   3 4  
2    2  2
2
 2
 2
2
3
4) Propiedades de la integral
a) El valor de la integral definida depende de los límites de integración y no de la variable
independiente:


b
a
b
a
f ( x) dx   F ( x) a
b
f (t ) dt   F (t ) a
b
b) Si se invierten los límites de integración, cambia el signo de la integral pero no el valor
absoluto.
c) Si c y d son dos puntos intermedios del intervalo (a, b), entonces:

b
a
c
d
b
a
c
d
f ( x) dx  f ( x) dx   f ( x) dx   f ( x) dx
Desarrollando el segundo miembro de la igualdad, obtenemos:
 F ( x)a   F ( x)c   F ( x)d  F  c   F  a   F  d   F (c)  F  b   F  d   F b   F  a 
c
d
b
5) Integral definida por sustitución
Al resolver una integral definida por sustitución, hay que cambiar los límites de integración.
Ejemplo:

2
2
dx 
2
x 3

7
dt
7
7
  ln t 4  ln 7  ln 4  ln
4
1
4 t
 x 1 t  4
t  x2  3  
x  2  t  7
dt  2 x dx
6) Integral definida por partes
Para la integral por partes, hallamos la integral indefinida y después sustituimos:

b
a
f  x  dx  u  v a   v du
b
b
a
7) Áreas de recintos limitados por dos líneas
Consideremos la superficie S limitada por las dos gráficas, entonces:
S  superficie  aAcBb   superficie  aAdBb    f  x  dx   f  x  dx 
b
b
a
a
 S    f  x   g  x   dx
a
b
y = g(x)
B
S
y = f(x)
A
a
b
Para hallar los límites de integración se resuelve el sistema formado por las dos ecuaciones.
Ejercicios:
a) Halla por integración el área del triángulo que determina la recta 2x + 5y = 10, al cortar con
los ejes coordenados
b) Halla por integración el área de un círculo de radio r
x 0 sen t 0; t 0
x 2 y 2 r 2 x r sen t
y
r 2 x 2 dx r cos tdt x r sen t 1; t
2
A
4
c)
d)
e)
f)
g)
r
r2
x 2 dx
0
2
r2
r 2 sen 2 t r cos t dt
0
r2
2
cos 2 t dt
0
2
r2 2
r2
1
r2
r2 A
1 cos 2t dt
t
sen 2t
2 0
2
2
2 2
4
4
0
2
Halla el área limitada por las líneas y = 3x; y = x
2
Halla el área limitada por la curva y  x  e x el eje OX, la ordenada en x = 0 y la ordenada
en el máximo
Halla el área de la porción de plano comprendida entre la curva y = 3x3–3x2+x+6 y su
tangente en el punto x = y
1
x
Halla el área limitada por las gráficas de las funciones: f  x   1  y g  x    x  1 2
3
x
Halla el área limitada por las líneas: f  x   x e , y = 0, x = 0 x = 1
1
 cos x , el eje OX y las rectas x = 0 y x = π
2
1
i) Halla el área limitada por la curva f  x  
y las rectas x = –1 y x = ½
4  x2
j) Halla el área del recinto limitado por las curvas f  x   sen x y las rectas x = 0, y = 0, x = 2π
h) Halla el área limitada por la función f  x  
k) Halla el área comprendida entre la recta x = 1 y las curvas y  x 2 , y 
8
x

 ln  x  x 1 dx
1
l) Halla:
dx
1 x  5 x  6
2
1
m) Halla:
2
1
1
el eje OX y las rectas x = 2, x  2 3
4  x2
o) Determinar f(x) sabiendo que f   x   24 x, f   0   2, f  0   1, f 0   0
n) Halla el área comprendida entre y 


p) Se tiene a   x sen 2 x dx y b   x cos 2 x dx
2
0
2
0
Nota: Hallar: a + b, a – b y obtener los valores de a y b
q) Hallar el área del recinto limitado por las curvas y  x 2  4 x, y  2 x  5
8) Volumen de un cuerpo de revolución
Dividimos el intervalo (a, b) en n partes
iguales y trazamos sus ordenadas
correspondientes. El volumen engendrado
por la superficie aABb al girar 360º
alrededor del eje OX es igual a la suma de
los volúmenes engendrados por los infinitos
rectángulos. Cada uno de ellos engendra un
cilindro de altura x  dx y radio de la base
f(x). El volumen de un cilindro elemental
viene
dado
por:
dV    f  x   dx : V  
2
2
  f  x  dx
b
a
Ejemplos:
a) Halla por integración el volumen de un
a
b
cono de radio r y altura h
b) Volumen de una esfera de radio r
9) Longitud de un arco de curva plana
Sea AB un arco de la curva y = f(x), y en él un arco elemental dl (arco de longitud infinitamente
pequeño) en el límite la longitud de un arco y su cuerda se confunden
dl
A
B
dy
dx
a
dl
dx
2
b
l
1
b
dy
2
dx 2
dy 2 dx
dx
2
1
dy
dx
dx
1
y 2 dx
y 2 dx
a
Ejercicios:
a) Hallar la longitud de la circunferencia de radio r
x
b) Calcular; F x
10t dt y después resolver F(2)
0
8
; hallar a y b para que la curva pase por el punto (–2, –6)
x
y admita en ese punto una tangente horizontal. Hallar el área engendrada por la curva el eje
OX y las rectas x = 1, x = 2
1 2
x 2
d) Hallar: 2 2
dx
0 x
1
e) Dada la función y x x 2 bx c , hallar b y c para que presente un máximo en x = 1, un
c) Dada la función f x
ax
b
mínimo en x = 3 y calcular el área limitada por la curva y el eje OX
f) Hallar el área limitada por la curva y 3 2 x 2 x3 y el eje OX
Hallar la longitud del arco de la parábola x2 =8y comprendido entre x = 0 y x =