PROBLEMAS FÍSICA Y QUÍMICA 1º BACHILLERATO

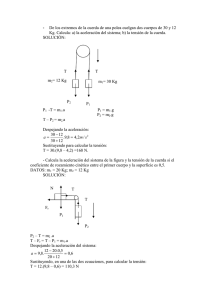
PROBLEMAS FÍSICA Y QUÍMICA 1º BACHILLERATO
RELACIÓN Nº 7: DINÁMICA (II)
MOVIMIENTO DE CUERPOS UNIDOS POR CUERDAS
1.- Por la garganta de una polea pasa una cuerda de cuyos extremos penden masas de 10
y 15 Kg. Suponiendo que no tiene masa la polea y que el rozamiento es despreciable.
Calcula: a) la aceleración del sistema, b) la tensión de la cuerda, c) el tiempo necesario
para que las masas se separen 2 m. Sol: a= 1,96 m/s2, T= 117,7 N, t= 1,43s.
2.- De los extremos de la cuerda de una polea cuelgan dos cuerpos de 30 Kg y 12 Kg.
Calcular:
a) La aceleración del sistema.
b) La tensión de la cuerda.
Sol: a) a= 4,2 m/s2; b) T= 168,3 N.
3.- Un bloque de 4,5 Kg descansa sobre un plano inclinado de 30º, unido mediante una
cuerda que pasa por una polea a un segundo cuerpo de 2 kg suspendido verticalmente.
Calcular la aceleración del sistema y la tensión de la cuerda. Sol:a=0,38m/s2;T=20,4N.
4.-Calcula la aceleración del sistema de la figura y la tensión de la cuerda si: a) no hay
rozamiento; b) el coeficiente de rozamiento cinético entre el cuerpo 1 y la superficie es
de 0,3.
m1= 15 Kg
m2= 10
Kg
= 20º
Sol: 1´9 m/s2; 79,1 N; 0´25 m/s2; 95´6 N
5. Si el coeficiente de rozamiento entre la masa m1 y el plano inclinado (ver figura) es
= 0,4 ¿cuál será la aceleración del sistema y la tensión del hilo?
Datos: m1= 1 Kg; m2= 200 g; sen = 0,6; cos= 0,8.
m2
m1

Sol: 0´66 m/s2; 2´09 N
6.- Sobre un plano inclinado 45º sin rozamiento, descansa un cuerpo de 15 Kg de masa
unido mediante una cuerda que pasa por la garganta de una polea a otro cuerpo de 5 Kg.
¿En qué dirección y con qué aceleración se moverá el conjunto? ¿Cuál será la tensión de
la cuerda? Sol: a=2,75 m/s2; T=62,8N
7.-Un cuerpo de masa m2=6 Kg se halla sobre un plano inclinado 30º y está unido,
mediante una cuerda ligera que pasa por una polea, a otro cuerpo de masa m1=2 Kg que
1
pende verticalmente. Calcula la aceleración con que se mueve el sistema y la tensión de
la cuerda que une los dos cuerpos.
Sol: a= 1,22 m/s2; T= 22 N.

8.-Sobre una mesa horizontal sin rozamiento y por la acción de la fuerza F se desliza un
sistema de dos masas de 6 y 2 Kg. Sabiendo que la aceleración del conjunto es 3,5 m/s2,

averigua el valor de F . La tensión de la cuerda, ¿depende del cuerpo al que se aplica la

fuerza F ? Sol: 28 N
9.- En un plano inclinado un ángulo respecto a la horizontal y sin rozamiento se
encuentra un bloque de masa M=10 Kg, unido por una cuerda que pasa a través de una
polea a otro bloque de masa m=2 Kg. Calcular:
a) El valor del ángulo para que el sistema esté en reposo.
b) La tensión de la cuerda en esas condiciones.
c) Se sitúa sobre el bloque de masa m otro bloque de masa m1= 1Kg. ¿Con qué
aceleración se mueve ahora el sistema?
d) En la nueva situación hallar la nueva tensión de la cuerda.
Sol: a) =11º32’; b) T=19,62 N; c) a=0,75 m/s2; d) T= 27,18 N.
10.- Dos bloques, de 8 Kg y 4 Kg, respectivamente, que están unidos por una cuerda,
deslizan hacia abajo sobre un plano inclinado de 30º. Los coeficientes de rozamiento
dinámico entre ambos bloques y el plano son, respectivamente, 0,25 y 0,40. Calcular:
a) La aceleración de cada bloque.
b) La tensión de la cuerda.
Sol: a) a= 2,35 m/s2; b) T= 3,4N.
DINÁMICA DEL MOVIMIENTO CIRCULAR
11.-Una piedra de 0,2 Kg, sujeta a una cuerda describe un círculo de 75 cm de radio en
un plano vertical. La tensión de la cuerda en el punto más alto es de 9 N. Calcula:
a) La fuerza centrípeta y la velocidad de la piedra en el punto más alto.
b) Averigua si se romperá la cuerda sabiendo que la velocidad en el punto más bajo es
de 10 m/s y que la tensión máxima que puede soportar es de 30 N.
Sol: a) Fc=10,96 N; v= 6,4 m/s; b) T= 28,56 N, no se romperá.
12.- Se ata una bola de 0,5 Kg de masa al extremo de una cuerda de 1,5 m de longitud y
se hace girar en un plano horizontal, sobre el que se apoya y con el que no tiene
rozamiento, con velocidad constante de 10 m/s. Calcula la tensión de la cuerda.
Sol: T= 33,3 N.
13.- Se ata una bola al extremo de una cuerda de 50 cm de longitud y se hace girar en el
aire con una velocidad constante en módulo. Si la cuerda forma un ángulo de 30º con la
vertical, calcula el módulo de la velocidad de la bola y el tiempo que tarda en dar una
vuelta completa. Sol: v= 1,2 m/s; t= 1,3 s.
14.- Se ata una bola al extremo de una cuerda de 75 cm de longitud y se hace girar en el
aire con una velocidad constante en módulo. Si la cuerda forma un ángulo de 45º con la
vertical, calcula el módulo de la velocidad de la bola. Sol: v= 2,3 m/s.
2
15.- Se ata una bola al extremo de una cuerda de 45 cm de longitud y se hace girar en el
aire con una velocidad constante en módulo. Si la cuerda forma un ángulo de 35º con la
vertical, calcula el tiempo que tarda en dar una vuelta. Sol: t= 1,2 s.
16.- Una bola de masa 200 g, sujeta a una cuerda de longitud 1,5 m, se hace girar en el
aire a velocidad constante, de modo que describe un péndulo cónico.
a) Si la cuerda forma un ángulo de 30º con la vertical, ¿cuánto tiempo tarda la bola en
dar una vuelta completa?
b) ¿Qué ángulo forma la cuerda con la vertical si la velocidad de la bola aumenta hasta
v= 4 m/s?
c) ¿Cuánto vale en este caso la tensión de la cuerda?
Sol: a) t= 2,3 s; b) 53,8º; c) T=3,3 N.
17.-Un automóvil de 1800 Kg de masa toma una curva plana de 100 m de radio a una
velocidad de 99 Km/h. Calcula la fuerza de rozamiento que existe entre los neumáticos
y la carretera. Sol: Fr= 13612,5 N.
18.-Un automóvil de 1400 Kg mantiene una velocidad de 90 km/h. Sabiendo que el
coeficiente de rozamiento de los neumáticos contra el suelo es 0,25, calcular:
a) La fuerza máxima de frenado cuando las ruedas se bloquean.
b) La distancia que recorre hasta pararse si frena en esas condiciones.
c) La velocidad máxima que puede tomar una curva no peraltada de 360 m de radio sin
que el coche derrape.
Sol: a) F= 3433,5 N; b) s= 127,5 m; c) v= 29,7 m/s.
19.- Un coche de 1000 Kg circula por una carretera horizontal sin peraltar y toma una
curva de 50 m de radio a una velocidad de 15 m/s. Si el coeficiente de rozamiento
contra el suelo es 0,4, ¿tiene peligro de derrape? ¿Y si la curva está peraltada un ángulo
de 30º? Sol: Fc= 4500N y Fr= 3924N, si hay peligro; b) v= 24,97 m/s.
20.- Calcula el coeficiente de rozamiento neumáticos-suelo para que un vehículo de 1
tonelada tome una cuerva de radio de giro 50 m a 80 km/h sin salirse. Sol: =1,01
21.- Calcula la velocidad máxima de un vehículo que toma una curva de 50 m de radio
con un peralte de 15° si el coeficiente de rozamiento es cero y la masa del vehículo 1 t.
Expresa el resultado en m/s y en km / h. Sol: v= 11,5 m/s.
3