Hallar el centro radical de las circunferencias

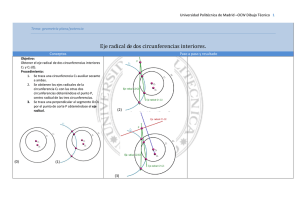
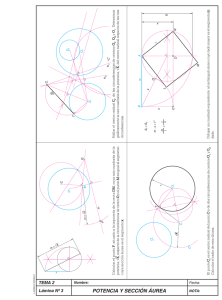
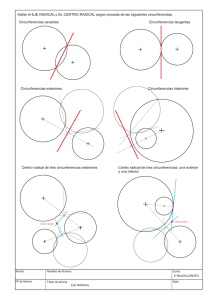
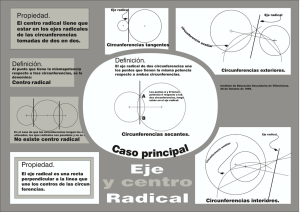
Problema realizado por Javier Chiquero
Enunciado:
Hallar el centro radical de las circunferencias:
c1: x2 + y2 +2x – 4y = 0
c2: x2 + y2 – 2x = 0
c3: x2 + y2 + 2x – 6y – 16 = 0
Teoría:
•
Una circunferencia es el lugar geométrico de los puntos del plano que
equidistan de un punto fijo llamado centro. La distancia al centro, se
llama radio.
•
Centro radical de tres circunferencias: Es el punto del plano que tiene
igual potencia respecto de las tres circunferencias (si los centros están
alineados, no hay centro radical, porque los ejes son paralelos).
C1 : x 2 + y 2 + Dx + Ey + F = 0
C2 : x 2 + y 2 + D' x + E' y + F' = 0
C3 : x 2 + y 2 + D' ' x + E' ' y + F' ' = 0
C1 - C2 : (D - D' )x + (E - E' )y + (F - F' ) = 0
Î Es una recta
c2 − c3 = (D'− D' ' )x + (E'−E' ' )y + F'− F' ' = 0
Î Es otra recta
Se resuelve el sistema formado por las dos rectas resultantes para hallar
el punto de corte entre ambas, que será el centro radical.
Resolución gráfica:
1. Se dibujan las circunferencias: Dibujamos su centro, y con la longitud del
radio, trazamos
2. Se trazan los ejes radicales: por los puntos en que se cortan las
circunferencias, trazamos rectas, que son los ejes radicales.
3. Se marca el punto de corte entre los ejes, el cual es el eje radical
Cálculo:
1. Restamos las ecuaciones de las circunferencias c1 y c2 para obtener uno
de los ejes radicales:
c1 : x 2 + y 2 + 2x − 4y = 0


−
4x − 4y = 0
c2 : x 2 + y 2 − 2x = 0



2. Restamos ahora las ecuaciones de las circunferencias c2 y c3 para
obtener el segundo eje radical:
c2 : x 2 + y 2 − 2x = 0



−
 - 4x + 6y + 16 = 0
c3 : x 2 + y 2 + 2x − 6y − 16 = 0


3. Resolvemos el sistema formado pos las dos rectas, despejando una
incógnita en una y sustituyéndola en la otra.
4y 

4x − 4y = 0 ⇒ x =   4y 
4  − 4  + 6y + 16 = 0

− 4x + 6y + 16 = 0
  4 
− 16y
+ 6y + 16 = 0
4
y = −8 ⇒ x =
4y
⇒ x = −8
4
Soluciones:
1. Primera recta: 4x − 4y = 0
2. Segunda recta: − 4x + 6y + 16 = 0
3. Intersección de las rectas, centro radical, y por tanto solución del
problema: C ( - 8 , 8 )