Descargar
Anuncio

CÓMO SE USA ESTE LIBRO
El libro contiene 14 unidades didácticas. Cada unidad
didáctica se inicia con una gran imagen motivadora, un
breve índice de contenidos con los epígrafes o apartados
que presenta el tema y un breve texto de introducción
con algunos ejemplos de aplicación de los contenidos tratados en la unidad.
u11
Estadística
223
1. Estadística
unidad 11 Estadística
contenidos
Desde los comienzos de la civilización han
existido formas sencillas de estadística. Hacia el año 3 000 a. C., los babilonios usaban
tablillas de arcilla para recopilar datos y los
egipcios analizaban los datos de la población. En cuanto a los griegos, realizaban
censos cuya información se utilizaba para
cobrar impuestos.
1. Estadística
2. Gráficos estadísticos
3. Parámetros estadísticos
4. Distribuciones de probabilidad
discretas
5. Distribuciones de probabilidad
continuas
En España, los primeros censos se remontan al siglo XVI.
6. Distribuciones bidimensionales
La estadística se desarrolla fundamentalmente a partir de los años 30.
En nuestros días, la estadística es ya un
método efectivo para describir los valores
de datos económicos, políticos, sociales…
y sirve como herramienta para relacionar
y analizar dichos datos. El trabajo estadístico no consiste solo en reunir y tabular
los datos, sino también en interpretar esa
información.
La estadística es la parte de las matemáticas que se ocupa del estudio de fenómenos mediante la recogida de datos, la organización, el análisis y la interpretación de resultados. Así, un estudio estadístico consta de cuatro fases:
Al conjunto de los datos estadísticos
recopilados se le llama distribución
estadística.
1. Recogida de datos.
2. Organización y representación gráfica.
3. Análisis.
Población es el conjunto de todos
los elementos de los que trata el estudio estadístico.
4. Obtención de conclusiones.
El estudio se puede realizar sobre una población entera o sobre una muestra.
A cada elemento se le llama individuo.
1.1. Variables
Se llama variable a la característica que queremos estudiar de los elementos
de una población.
Las variables pueden ser:
• Cualitativas: son las que no toman valores numéricos: color de ojos, sexo,
raza, profesión…
• Cuantitativas: son las que toman valores numéricos: número de hijos, altura, peso, número de goles…
Estas, a su vez, pueden ser:
Muestra es un subconjunto representativo de la población.
Recorrido es la diferencia entre los
valores extremos de una variable estadística.
– Discretas: la variable discreta es la que toma un número finito de valores, es decir, entre dos valores consecutivos no existe ningún otro valor.
EJEMPLO
• El número de hijos es una variable discreta, ya que se pueden tener 1,
2, 3, 4…, pero no hay valores intermedios (2,3 hijos, por ejemplo).
– Continuas: la variable continua es la que toma un número infinito de valores, es decir, entre dos valores consecutivos siempre existe otro valor.
Amplitud de un intervalo es la diferencia entre los valores extremos
del intervalo.
EJEMPLO
• La altura de los jugadores de un equipo de baloncesto es una variable
continua. Entre 190 cm y 195 cm hay infinitos valores: 191, 192, 192,5…
Si la variable estadística es continua, conviene agrupar los valores en intervalos. Para ello, dividimos el recorrido en tantas partes iguales como intervalos
queramos. Al valor del punto medio de cada intervalo se lo denomina marca
de clase y es el que se toma para realizar los cálculos.
EJEMPLO
• Un hospital hace un estudio sobre el peso de los bebés al nacer. Es una variable continua cuyo recorrido va desde 2 100 g hasta 4 820 g. Hacemos intervalos de 500 g.
Intervalos
2 000/2 500
2 500/3 000
3 000/3 500
3 500/4 000
4 000/4 500
4 500/5 000
2 250
2 750
3 250
3 750
4 250
4 750
Marca de clase
→
A continuación, comienza el desarrollo de contenidos ordenado en epígrafes y subepígrafes y acompañados de
numerosas fotografías, gráficos y ejemplos, que son ejercicios resueltos explicados de forma rigurosa, para hacer
más compresibles y amenos los diferentes aprendizajes.
Unidad 11 →
224
Una vez recogidos los datos, los organizamos en tablas de frecuencia.
• La frecuencia absoluta fi es el número de veces que aparece un determinado valor en un estudio estadístico. La suma de todas las frecuencias absolutas es igual al número de datos.
EJEMPLO
La variable se representa como xi y
se lee «equis sub i».
• Estudiamos el número de suspensos en una clase de 30 alumnos:
2, 0, 1, 3, 0, 0, 1, 0, 5, 0, 1, 2, 0, 0, 4, 1, 3, 0, 2, 1, 6, 1, 0, 0, 0, 2, 0, 1, 0, 1.
Calcula las frecuencias absolutas.
La frecuencia absoluta se representa por fi.
xi
0
1
2
3
4
5
6
suma
fi
13
8
4
2
1
1
1
30
• La frecuencia relativa hi de un determinado valor xi es el cociente entre la
f
frecuencia absoluta y el número total de datos: h i = i .
N
Si entre el valor mayor y el menor hay
algún valor posible que no aparece,
también lo debemos escribir.
EJEMPLO
• Calcula la frecuencia relativa y la frecuencia relativa en porcentaje del ejemplo anterior.
xi
0
1
2
3
4
5
6
fi
13
8
4
2
1
1
1
hi
8
2
13
4
1
1
1
= 0, 43
= 0, 27
= 0,13
= 0, 07
= 0, 03
= 0, 03
= 0, 03
30
30
30
30
30
30
30
%
43 %
27 %
13 %
7 %
3 %
3 %
EJEMPLO
• Calcula la frecuencia absoluta acumulada del ejemplo anterior.
Fi = f1 + f2… fi
Fi
13
21
25
27
28
29
30
• La frecuencia relativa acumulada Hi de un determinado valor xi es la suma
de su frecuencia relativa más las frecuencias relativas inferiores a xi.
En la frecuencia absoluta acumulada, el último valor coincide con el
número total de datos.
EJEMPLO
• Calcula la frecuencia relativa acumulada del ejemplo anterior.
Hi = h1 + h2… hi
Hi
0,43
0,70
0,83
0,90
0,93
0,96
0,99
ACTIVIDADES
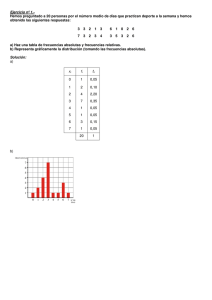
1. El número de horas que dedican
al estudio un grupo de alumnos
es 3, 1, 2, 3, 2, 1, 2, 0, 3, 4, 2, 2,
3, 1, 3, 2, 3, 1, 4, 2, 3, 3, 2, 1, 5.
Los gráficos más comunes son:
• Diagrama de barras: se utiliza para variables discretas.
– Dibujamos un eje de coordenadas.
– En el eje de abscisas representamos los valores de la variable xi y en el eje
de ordenadas las frecuencias.
– Se levantan barras verticales separadas que tienen la misma anchura y la
altura de la frecuencia.
EJEMPLO
xi
fi
1
3
Organiza los datos en una tabla
de frecuencias.
2. Representa en un diagrama adecuado los datos del ejercicio anterior.
10
• Representa en un diagrama de barras los resultados de un estudio estadístico sobre el número de libros leídos por un grupo de alumnos.
2
5
3
9
4
3
En los diagramas de barras se pueden utilizar frecuencias absolutas,
frecuencias relativas o frecuencias
porcentuales.
8
6
4
Si las frecuencias son muy elevadas,
conviene «tumbar» las barras, con
lo que se consigue un diagrama de
barras horizontal.
2
5
0
1
2
3
4
5
• Diagrama de sectores: los datos se representan en un círculo de manera que
la frecuencia sea proporcional al área del círculo. En un diagrama de sectores, los ángulos centrales de los sectores circulares son proporcionales a las
frecuencias.
EJEMPLO
• Representa en un histograma los
datos de la altura de los jugadores de un equipo de baloncesto.
EJEMPLO
• Representa en un diagrama de sectores los resultados
de fútbol a lo largo de un año.
xi
1
x
2
3 %
• La frecuencia absoluta acumulada Fi de un determinado valor xi es la suma
de su frecuencia absoluta más las frecuencias absolutas inferiores a xi.
La frecuencia relativa se puede expresar en porcentaje multiplicando
por 100.
225
Al realizar un estudio estadístico se obtiene gran cantidad de datos y, aunque
los agrupamos en tablas, también se pueden expresar mediante gráficos que nos
dan una idea más clara y sencilla de los resultados.
La suma de todas las frecuencias relativas es igual a 1.
Los márgenes incluyen información complementaria que
pueden contener ampliación de contenidos y curiosidades.
Para ampliar conocimientos y comprobar si se han entendido los contenidos analizados con anterioridad, se plantean diversas Actividades, numeradas correlativamente
desde el inicio de la unidad.
Estadística
2. Gráficos estadísticos
1.2. Tablas de frecuencia
El número total de datos se representa con la letra N.
fi
5
(180-185] 1
xi
4
(185-190] 2
fi
300
200
100
3
(190-200] 5
2
(200-205] 3
1
(205-210] 1
(180
-185]
• Histograma: se utiliza para variables continuas o discretas agrupadas en intervalos.
– Dibujamos un eje de coordenadas.
– En el eje de abscisas representamos los intervalos de la variable xi y en el
eje de ordenadas las frecuencias.
– Si todos los intervalos tienen la misma amplitud, dibujamos rectángulos
de igual anchura y de altura igual a la frecuencia. Si tienen diferente amplitud, el área de los rectángulos debe ser proporcional a la frecuencia. No
se deja espacio entre los rectángulos
(185
-190]
(190
-200]
(200
-205]
(205
-210]
EJEMPLO
• Representa en un polígono de frecuencias el número de accidentes
de moto durante la semana en una
localidad.
xi
fi
L
2
M X
1 3
J
1
V
8
S
7
D
4
J
V
S
D
8
• Polígono de frecuencias: se puede usar para variables discretas y continuas.
– Dibujamos un eje de coordenadas.
– En el eje de abscisas representamos la variable xi y en el eje de ordenadas
las frecuencias.
– Se dibujan los puntos y se unen mediante segmentos.
6
4
2
L
M
X
→
La aplicación práctica de los conceptos, se plasma en el
apartado de Actividades resueltas que contiene cada
una de las tipologías de actividades fundamentales de
la unidad.
Unidad 11 →
240
Estadística
241
ACTIVIDADES RESUELTAS
1. Las edades de 20 niños son 13, 14, 6, 8, 10, 10, 11, 11, 14, 12, 7, 9, 9, 12, 12, 9, 13, 8, 10, 7. Organiza los datos en
una tabla de frecuencias y calcula la media, la moda y la mediana. Representa los datos en un gráfico adecuado.
xi
6
7
8
9
10
11
12
13
14
Suma
fi
1
2
2
3
3
2
3
2
2
20
hi
0,05
0,1
0,1
0,15
0,15
0,1
0,15
0,1
0,1
1
Fi
1
3
5
8
11
13
16
18
20
Hi
0,05
0,15
0,25
0,4
0,55
0,65
0,8
0,9
1
6
14
16
27
30
22
36
26
28
xi fi
∑xf
i i
x =
Mo = hay tres modas: 9, 10 y 12.
N
=
Mediana: se calcula el valor central. Como el número de datos es par, se usa la fórmula
El rango es la diferencia entre el mayor y el menor de los datos: R = 14 – 6 = 8.
Ampliamos la tabla de frecuencias con los valores que necesitamos.
|xi – x–| fi
xi2 fi
Dm =
∑x
σ =
∑x f
205
205
= 10, 25.
20
Media:
Moda:
3. Con los datos del ejercicio 1, calcula el rango, la desviación media, la desviación típica y el coeficiente de variación.
N
N
y
+ 1.
2
2
El valor central es la media aritmética de 10 y 11, que es 10,5. Se busca la frecuencia absoluta mayor a 10,5 y se mira a qué
valor de la variable se corresponde; en este caso es 10, por lo que Me = 10.
Como la variable es discreta, el gráfico más adecuado será un diagrama de barras.
i
− x fi
N
2
i i
N
=
4,25
6,5
36
98
39, 5
= 1, 975
20
4,5
128
σ2 =
3,75
0,75
1,5
5,25
5,5
7,5
39,5
243
300
242
432
338
392
2 209
∑x f
2
i i
N
− x2 =
2 209
− 105, 06 = 5, 39
20
σ
2, 32
=
= 0, 226
Cv =
10, 25
x
− x 2 = 2, 32
4. En una guardería con 20 niños falta a clase cada uno de ellos el 10 % de los días. Calcula la probabilidad de que
un día no falte ninguno y la probabilidad de que falten menos de cinco niños.
n = 20
k=0
p = 0,10
q = 0,90
B (20, 0,10)
P (x = 0) = 20 0,100 ⋅ 0, 9020 = 0,12
0
La probabilidad de que falten menos de 5 será la probabilidad de que no falte ninguno más la de que falte 1 o 2 o 3 o 4.
P (x < 5) = P (x = 0) + P (x = 1) + P (x = 2) + P (x = 3) + P (x = 4).
3
P (x < 5) = 0,12 + 20 0,11 ⋅ 0, 919 + 20 0,12 ⋅ 0, 918 + 20 0,13 ⋅ 0, 917 + 20 0,14 ⋅ 0, 916.
1
2
4
3
2
P (x < 5) = 0,12 + 0,27 + 0,29 + 0,19 + 0,09 = 0,96.
1
0
6
7
8
9
10
11
12
13
14
5. En un pueblo, dos de cada tres familias tienen Internet en casa. Si elegimos 90 familias, calcula la probabilidad
de que al menos 60 tengan Internet.
n = 90
2. Halla la media, la varianza y la desviación típica de una variable X cuya función de probabilidad es:
x
1
3
4
pi
0,2
0,3
0,5
p = 2/3
q = 1 – p = 1/3
Como se tiene en este caso que: n · p = 90 · 0,66 = 59,4 ≥ 5.
n · q = 90 · 0,33 = 29,7 ≥ 5.
La distribución binomial B (90, 0,66) será aproximable a una distribución normal N = (60, 4,47).
Si calculamos la probabilidad de que como mínimo 60 familias tengan Internet instalado:
Ampliamos la tabla de frecuencias con los valores que necesitamos.
µ =
∑ x p = 3,1
∑x p − µ
σ2 =
σ =
i
i
∑x p
2
i i
2
xi pi
0,2
0,9
2
3,1
xi2 pi
0,2
2,7
8
10,9
6. La recta de regresión de y sobre x de una distribución estadística es y = 2,87x + 13,44. Calcula una estimación para
x = 18.
i
2
i
60 − 60
p (x > 60) = p Z >
= p (Z > –0) = 1 – p (Z ≤ 0) = 0,5.
4, 47
= 10, 9 – 9, 61 = 1, 29
− µ 2 = 114
,
y = 2,87 · 18 + 13,44
→
y = 65,1.
Para x = 18 se estima una y = 65,1.
→
Pruebas acceso FP Matematicas Primeras.indd 4
05/03/14 18:43
IMPORTANTE: Todas las actividades propuestas en este libro deben
realizarse en un cuaderno de trabajo, nunca en el propio libro.
Las páginas de Actividades finales incluyen ejercicios
y problemas agrupados por contenidos que permiten
evaluar los contenidos y afianzar el aprendizaje. Estas
actividades están clasificadas en tres niveles de dificultad mediante los siguientes símbolos:
Unidad 11 →
242
Estadística
243
ACTIVIDADES FINALES
Variables, gráficos y tablas de frecuencia
○ 1.
◐ 9.
Una variable aleatoria x toma los valores 2, 3, 5, 7, 8, 9 con probabilidades 0,1; 0,3; 0,15; 0,25; 0,12; 0,08 respectivamente.
Comprueba que es una función de probabilidad y halla la media y la desviación típica.
Indica si las variables siguientes son cualitativas o cuantitativas y si son discretas o continuas.
a) Número de hijos por familia en una determinada población.
Distribuciones de probabilidad continuas
b) Color de pelo de un grupo de chicas.
● 10. La vida media de un teléfono móvil es de 2 años con una desviación típica de 0,3 años. Si la vida media de los teléfonos
c) Peso de los jugadores de un equipo de fútbol.
móviles sigue una distribución normal, halla la probabilidad de que al comprar un teléfono móvil, este dure más de 3 años.
d) Grupo sanguíneo de los miembros de una familia.
● 11. El tiempo empleado por los alumnos de un instituto en llegar desde sus casas sigue una distribución normal de media
e) Número de viajeros que usan a diario el puente aéreo.
15 min y desviación típica 5 minutos. Calcula cuál sería la probabilidad de que el tiempo de llegada esté entre 10 y 20 min.
f) Altura de los jugadores de un equipo de baloncesto.
○ 2.
Agrupa los siguientes datos en cuatro intervalos iguales y construye una tabla de frecuencias.
Distribuciones bidimensionales
0; 1,25; 1,80; 2,25; 3,4; 1; 0,64; 0,25; 0,75; 3,16; 0,68; 3,43; 2,32.
○ 3.
● 12. La siguiente tabla muestra las notas de 6 alumnos de física y matemáticas.
Representa los siguientes datos en un diagrama adecuado.
Intervalo
Frecuencia
(0,2]
(2,4]
(4,6]
(6,8]
(8,10]
2
4
8
5
1
Física
6
4
3
4
8
5
Matemáticas
7
5
4
6
9
5
a) Calcula el coeficiente de correlación lineal e interpreta el resultado.
○
Sencilla
Parámetros de centralización
○ 4.
Calcula la media, la moda y la mediana de los siguientes datos estadísticos.
◐
Media
○ 5.
A continuación se muestran los datos del número de hermanos que tienen los alumnos de una clase: 1, 3, 2, 2, 2, 3, 3, 4,
0, 1, 1, 1, 2, 3, 2, 6, 3, 2, 2, 1, 0, 3, 3, 1, 2.
●
Difícil
b) Calcula la recta de regresión de Y sobre X y de X sobre Y. Halla el punto de corte de las 2 rectas.
xi
10
12
15
18
25
30
fi
4
3
6
1
7
2
c) Representa gráficamente las 2 rectas.
d) Efectúa la estimación para x = 7.
e) Realiza la interpretación de los resultados.
AUTOEVALUACIÓN
a) Construye una tabla de frecuencias y representa los datos en un gráfico estadístico.
b) Calcula los parámetros de centralización.
◐ 6.
◐ 7.
Para completar la unidad se plantea una Autoevaluación
con preguntas tipo test que pone a prueba nuestros conocimientos. Las soluciones de estas autoevaluaciones se
encuentran al final del libro.
Como cierre de la teoría, En resumen nos presenta un
resumen conceptual muy práctico para organizar los
contenidos de la unidad. Este apartado nos sirve para
recapitular lo tratado en la unidad.
Calcula el recorrido, la varianza y la desviación típica de los siguientes datos estadísticos.
xi
10
14
17
20
23
25
fi
2
6
4
1
3
5
c) Punto medio.
b) Marca de clase.
d) Punto intervalo.
b) La muestra es 3 y la frecuencia absoluta es 15
Se ha hecho un estudio sobre el número de horas diarias que dedica un grupo de personas a ver la televisión. Las respuestas son las siguientes: 3, 2, 5, 4, 7, 1, 0, 3, 2, 2, 3, 4, 1, 2, 5, 3, 2, 0, 4, 1.
c) El valor de la variable con mayor frecuencia absoluta.
d) Siempre mayor que la media.
6. El coeficiente de variación es:
a) El cociente entre la desviación típica y la media.
c) La muestra es 15 y la frecuencia absoluta es 5
b) El cociente entre la media y la desviación típica.
d) La muestra es 15 y la frecuencia relativa es 3
c) El cociente entre la varianza y la desviación típica.
3. La media de la siguiente distribución estadística es:
b) Calcula los parámetros de dispersión.
Distribuciones de probabilidad discretas
Un estudio revela que un 15 % de los niños de 11 años ha probado alguna vez un cigarrillo.
xi
1
2
3
4
5
fi
4
5
6
2
4
a) 2,8
Si se eligen al azar 10 niños, calcula:
a) Probabilidad de que ninguno haya probado el tabaco.
b) 3
7. Para una variable xi que sigue una distribución binomial
B (4, 0,2), los valores de la media y de la desviación típica
son:
c) 3,2
a) 0,4 y 0,2
d) 3,4
a) Media.
c) Varianza.
c) ¿Cuál es el número medio de niños que se espera que hayan probado el tabaco si se eligen 100 niños al azar?
b) Mediana.
d) Moda.
b) 0,8 y 0,8
c) 4 y 2
d) 0,4 y 0,02
8. Se sacan 5 cartas de la baraja española con devolución
y miramos si son ases. ¿Cuál es la probabilidad de sacar
3 ases?
4. El valor que ocupa el valor central se llama:
b) Probabilidad de que al menos 8 hayan fumado alguna vez.
a) 0,81
b) 0,081
c) 0,0081
d) 0,00081
→
Unidad 11 →
244
Unidad 5 →
104
EN RESUMEN
EN RESUMEN
{
Variable
Cuantitativa
{
• Definición de sistema de ecuaciones lineales. Solución
Discreta
Unsistemademecuacioneslinealesconnincógnitas ( x1, x 2 , x3 ... x n ) serepresentadeformagenéricadelasiguiente
manera:
Continua
a11x1 + a12 x 2 + a13 x3 + ....... + a1n x n = b1
a x + a x + a x + ....... + a x = b
22 2
23 3
2n n
2
21 1
....................................................................
am1x1 + am 2 x 2 + am3 x3 + ....... + amn x n = bm , donde aij y bi (1 ≤ i ≤ m, 1 ≤ j ≤ n) sonnúmerosrealesconocidos.
Esunconjuntoenelcualsebuscaunasolucióncomúnatodaslasecuaciones.
Cualitativa
• Tablas de frecuencias:
Paraunsistemadedosecuacioneslinealescondosincógnitasx, y,lasolucióneselpardevaloresqueverificalasdos
ecuacionesalavez.Resolverelsistemaconsisteenencontrarlasolución.
– La frecuencia relativa hieselcocienteentrelafrecuenciaabsolutayelnúmerototaldedatos.
• Transformaciones que convierten un sistema en otro equivalente al dado
– La frecuencia absoluta acumuladaFieslasumadelasfrecuenciasabsolutasinferioresaxi.
– Multiplicarodividirunadelasecuacionesdelsistemaporunnúmerononulo.
– La frecuencia relativa acumulada Hieslasumadelasfrecuenciasrelativasinferioresaxi.
– Intercambiardeposicióndosecuacionesoincógnitasentresí.
– Gráficos estadísticos:diagramadebarras,diagramadesectores,histograma,polígonodefrecuencias.
{
– Sumarorestaraunaecuaciónunmúltiplodeotra.
• Parámetros estadísticos:
– Despejarenunaecuaciónunadelasincógnitasysustituirlaenotrasecuaciones.
• Tipos
de sistemas
– Moda:eselvalorquetienemayorfrecuenciaabsoluta.SerepresentacomoMo.
– Mediana:eselvalorqueocupaellugarcentraldetodoslosdatoscuandoestánordenadosdemenoramayor.
Se representacomoMe.
– Rango o recorrido:esladiferenciaentreelmayoryelmenordelosvaloresdelavariabledeunadistribución
estadística.SerepresentacomoR.
Sistemas de
ecuaciones
lineales
– Desviación media:eslamediaaritméticadelvalorabsolutodelasdesviacionesrespectodelamediadeuna
distribuciónestadística.SerepresentacomoDm.
– Varianza:eslamediaaritméticadelcuadradodelasdesviacionesrespectodelamediadeunadistribución
estadística.Serepresentacomos2.
– Desviación típica:eslaraízcuadradadelavarianza.Serepresentacomos.
– Coeficiente de variación:eselcocienteentreladesviacióntípicaylamedia.
• Parámetros de distribuciones de probabilidad discreta:
– Media:μ=n·pydesviacióntípica: σ =
{
{
{
– Añadiroeliminarunaecuaciónqueseacombinaciónlinealdelasdemásecuaciones.
– Media aritmética:eselvalorobtenidoalsumartodoslosdatosydividirelresultadoentreelnúmerototalde
datos.Serepresentacomo x.
n⋅p⋅q.
– Homogéneos
(Todos los bi = 0)
– No homogéneos
(algún bi ≠ 0)
• Métodos de resolución
• Parámetros de distribuciones de probabilidad continua:
– μ=0 y s=1. SerepresentacomoN(0,1).
{
– Compatibles.
Tienen solución
– Compatibles.
Tienen solución
–Determinados.
Lasoluciónesúnica
Gráfica:dosrectasquesecortan
enunpunto.
–Indeterminados.
Infinitassoluciones
Gráfica:
dosrectas
coincidentes.
–Determinados.
Lasoluciónesúnica
Gráfica:dosrectasquesecortan
enunpunto.
–Indeterminados.
Infinitassoluciones
Gráfica:
dosrectas
coincidentes.
– Incompatibles.
No tienen solución
Gráfica:dos
rectasparalelas.
– Por sustitución
P araresolverunsistemaporelmétododesustitución,sedespejaunaincógnitaenuna
delasecuacionesysesustituyesuvalorenlaotra.
– Por reducción
– Covarianza:eslamediaaritméticadelosproductosdelasdesviacionesdecadaunadelasvariablesrespecto
de susmedias.Serepresentacomosxy.
R
esolverunsistemaporelmétododereducciónconsisteenencontrarotrosistemacon
lasmismassolucionesquetengaloscoeficientesdeunamismaincógnitaigualesode
signocontrarioparaque,alrestarosumarlasdosecuaciones,laincógnitadesaparezca.
– Por igualación
– Correlación:eselgradodedependenciaqueexisteentrelasdosvariablesdeunadistribuciónbidimensional.
Se representacomor.
– Método de Gauss
P araresolverunsistemaporelmétododeigualación,sedespejalamismaincógnita
enlasdosecuacionesyseigualan.
a1x + b1y + c1z = p
ElmétododeGaussconsisteenobtenerun
sistemaequivalentealdadoqueseaescalonado:
b2 y + c 2 z = q .
c3 z = r
• Distribución bidimensional
– Recta de regresión:eslarectaquemejorseajustaalanubedepuntos.
Estadística
245
La recta
163
Nota (xi )
1
2
3
4
5
6
7
8
N.º de alumnos (fi )
3
4
5
7
8
5
4
3
9
1. a) Halle la ecuación de una recta que pase por el origen de coordenadas y el punto (–1, 3).
b) Halle la ecuación de una recta paralela a la que has obtenido en el apartado anterior y que pase por el punto (1, 9).
2. Una partícula se desplaza sobre un plano describiendo una trayectoria r en línea recta que pasa por los puntos (–5, 0) y (0, 2)
de un sistema de ejes cartesianos definido en el plano. Otra partícula se desplaza por el mismo plano a lo largo de la recta
s de ecuación –7x + 3y –6 = 0.
a) Determine la ecuación cartesiana de la recta r.
2. El peso medio de los jugadores de un equipo de fútbol es de 58 kg y su desviación típica es de 4 kg, mientras que la altura
media es de 175 cm y su desviación típica es de 5 cm.
b) Halle el punto de corte de ambas trayectorias.
Y
3. Sean los puntos A (1, 1), B (5, 2), C (4, 4) y D (0, 3) los vértices
de un paralelogramo.
3. Si z es una variable aleatoria que sigue una distribución normal N z (0, 1), ¿cuánto vale P (z ≤ 0)?
6
5
a) Halle la medida del ángulo A:
a) P (z ≤ 0) = 0
4
a) 95,32°
b) P (z ≤ 0) = 0,5
3
b) 102,53°
xi
1
2
3
4
5
N.º de animales
fi
20
50
80
70
30
a) x + 3y = 5
–6
–5
–4
–3
c) x + 5y = 15
1
2
3
4
5
6
X
–3
–4
a) Halla la ecuación de la recta que pasa por los puntos A y B.
b) Calcula la pendiente de la recta que pasa por los puntos A y B.
c) Indica cuál es la moda.
B
A
0
–1
–2
4. Dados los puntos A (2, –1) y B (5, 3).
b) Calcula la media.
–2
–1
b) x + 2y = 15
a) Elabora un diagrama de barras a partir de los datos de la tabla.
C
1
b) Halle la ecuación de la recta BD.
4. El número de animales que hay en una granja según el número de años de vida que tiene cada uno viene dado por la tabla:
D
2
c) 105°
c) P (z ≤ 0) = 1
N.º años de vida
A
1. En la tabla adjunta se recoge la distribución de las notas obtenidas en la asignatura de Matemáticas por los 40 alumnos de
una clase. Calcula la mediana, la moda, la media aritmética y la desviación típica de la variable:
EB
A
EB
U
U
PR
ACTIVIDADES DE PRUEBAS DE ACCESO
PR
ACTIVIDADES DE PRUEBAS DE ACCESO
Calcule los coeficientes de variación e indique en qué grupo hay más dispersión, en el de los pesos o en el de las alturas.
Regístrate en nuestra web y accede al Solucionario de
todas las actividades y a los recursos adicionales:
<www.editex.es>.
b) El valor de la variable con menor frecuencia absoluta.
3
, entonces:
15
a) La muestra es 15 y la frecuencia absoluta es 3
a) Construye una tabla de frecuencias y representa los datos en un gráfico estadístico.
◐ 8.
a) La frecuencia absoluta más alta.
a) Marca de intervalo.
2. Si la frecuencia relativa de una variable xi es
– La frecuencia absoluta fi eselnúmerodevecesqueapareceundeterminadovalor.
Para finalizar la Unidad, se presenta el apartado Actividades de pruebas de acceso, en el que se recogen actividades
correspondientes a pruebas de acceso de distintas comunidades autónomas.
5. La moda es:
1. Al punto medio de un intervalo se le llama:
Parámetros de dispersión
–5
–6
c) Calcula las coordenadas del punto medio del segmento que une los puntos A y B.
d) Determina el porcentaje de animales de la granja que tiene menos de 3 años.
d) Calcula la distancia entre los puntos A y B.
5. Los porcentajes de población activa dedicados a la agricultura en 30 países africanos son 47, 24, 70, 63, 91, 61, 63, 75, 56,
57, 68, 74, 77, 69, 68, 70, 75, 64, 37, 36, 65, 91, 62, 14, 66, 81, 24, 66, 63, 43.
5. Halla la ecuación de la recta que pasa por el punto (1, 1) y es paralela a la recta que pasa por los puntos A (1, 2) y B (3, –4).
6. Dada la recta de ecuación 3x – 2y + 6 = 0, realiza las siguientes cuestiones:
a) Agrupa estos datos en 5 intervalos de igual amplitud.
a) Pendiente de dicha recta.
b) Calcula la media, la moda y la mediana.
b) Puntos de corte con los ejes coordenados.
c) Calcula la varianza, la desviación típica y el coeficiente de variación.
c) Punto medio de los dos puntos obtenidos en el apartado anterior.
6. Se ha medido durante 16 días consecutivos la temperatura en grados centígrados del interior de una cámara de frío: 4, –1,
0, 4, 2, 0, 2, 0, 0, –1, 2, 2, 2, 2, 0, 4.
d) Ecuación de la recta que pasa por el origen de coordenadas y es perpendicular a dicha recta.
7. Dados los puntos A, B y P de coordenadas A (–3, 2), B (1, –1) y P (1, 4), calcula:
¿Cuál es la opción correcta?
a) x = 1,275 y R = 3
c) R = 5 y M = 3
b) Mo = 2 y x = 1,375
d) Mo = 6 y V = 2,73
a) La ecuación de la recta r que pasa por A y B.
b) La ecuación de la recta s perpendicular a la anterior y que pasa por el punto P.
c) El perímetro del triángulo formado por los puntos A, B y P.
Extracto de Pruebas de Acceso a Ciclos Formativos de Grado Superior:
País Vasco 2012 (1), Galicia 2012 (2 y 3), Extremadura 2011 (4),
Castilla-La Mancha (5), Canarias 2009 (6).
Extracto de Pruebas de Acceso a Ciclos Formativos de Grado Superior:
Navarra 2012 (1), Madrid 2012 (2), Galicia 2012 (3), Extremadura 2011 (4),
Castilla-La Mancha 2009 (5), Extremadura 2010 (6), Aragón 2012 (7).
←
←
→
Pruebas acceso FP Matematicas Primeras.indd 5
05/03/14 18:43