b - iesaricel.org
Anuncio
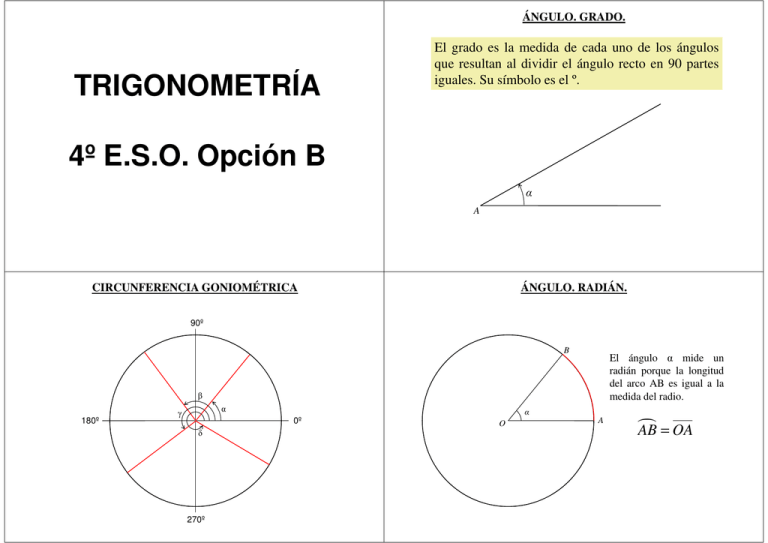
ÁNGULO. GRADO. TRIGONOMETRÍA El grado es la medida de cada uno de los ángulos que resultan al dividir el ángulo recto en 90 partes iguales. Su símbolo es el º. 4º E.S.O. Opción B α A CIRCUNFERENCIA GONIOMÉTRICA ÁNGULO. RADIÁN. 90º B El ángulo α mide un radián porque la longitud del arco AB es igual a la medida del radio. β 180º α γ α 0º δ 270º O A AB = OA PASO DE RADIANES A GRADOS Y VICEVERSA BC AB sen α = 360º = 2π radianes Paso de grados a radianes RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO cos α = AC AB tg α = BC AC Paso de radianes a grados B α grados = 2π ⋅ α radianes 360 n radianes = 360 ⋅ n grados 2π α 360 180 El valor de un radián es: = = 57º 17' 45'' 2π 3,1416 RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO A RAZONES TRIGONOMÉTRICAS DEL ÁNGULO 45º Los lados de un triángulo ABC miden 8, 15 y 17 centímetros, respectivamente. a) Comprueba si el triángulo es rectángulo. b) Halla las razones trigonométricas del ángulo agudo de mayor amplitud. 17 C c = x 2 + x 2 = 2x 2 = 2 x c x x a) Para que el triángulo sea rectángulo ha de cumplir el teorema de Pitágoras. 82 + 152 = 64 + 225 = 289 = 172 → El triángulo es rectángulo. cos 45º = x 1 2 = = 2 2x 2 tg 45º = b) En el triángulo el cateto opuesto al de mayor amplitud es el más grande, por tanto mide 15, y el cateto contiguo mide 8. 8 cos α = 17 x 1 2 = = 2 2x 2 45º 8 15 15 sen α = 17 sen 45º = 15 tg α = 8 sen 45º = 2 2 cos 45º = 2 2 x =1 x tg 45º = 1 RAZONES TRIGONOMÉTRICAS DEL ÁNGULO 60º RAZONES TRIGONOMÉTRICAS DEL ÁNGULO 30º 30º x 30º x x2 3x 2 3x h= x − = = 4 4 2 xh 60º 2 60º x/2 sen 60º = x2 3x 2 3x h= x − = = 4 4 2 xh 2 x/2 x 1 cos 60º = 2 = x 2 3x 2 = 3 x 2 sen 60º = 3 2 cos 60º = 1 2 tg 60º = 3x 2 = 3 x 2 x 1 sen 30º = 2 = x 2 sen 30º = tg 60º = 3 RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS cos 30º = 1 2 3x 2 = 3 x 2 cos 30º = 3 2 tg 30º = x 2 = 1 = 3 3 3x 3 2 tg 30º = 3 3 RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS B c a sen α c a = = = tg α cos α b b c a α A b tg α = B c C 2 2 2 2 2 2 1 sen α + cos α sen α cos α = = + = tg 2 α + 1 2 2 2 2 cos α cos α cos α cos α sen 2 α + cos 2 α = 1 α 2 2 2 c2 a b a +b sen α + cos α = + = = =1 c2 c2 c c 2 a sen α cos α A b C tg 2 α + 1 = 1 cos 2 α RELACIÓN ENTRE LAS RAZONES TRIGONOMÉTRICAS CIRCUNFERENCIA GONIOMÉTRICA Si el coseno de un ángulo α vale 2 , ¿cuál es el seno de este ángulo? ¿Y 3 la tangente? 90º Primer cuadrante cos α sen 2 α + cos 2 α = 1 A (cos α , sen α) 2 2 sen 2 α + = 1 3 2 sen 2 α = 1 − 3 7 sen 2 α = 9 sen α = Segundo cuadrante 7 sen α 7 14 = 3 = = tg α = cos α 2 2 2 3 2 sen α α 180º 0º Tercer cuadrante Cuarto cuadrante Las coordenadas del punto A son el valor de coseno y seno de α 7 3 270º RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA Halla el coseno y la tangente de α si sen α = 90º sen α ≥ 0 cos α ≤ 0 tg α ≤ 0 B cos β RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA cos α sen α ≥ 0 cos α ≥ 0 tg α ≥ 0 A 1 π y ≤ α ≤ π. 3 2 sen 2 α + cos 2 α = 1 2 sen β β α γ 180º 1 2 + cos α = 1 3 sen α 0º δ sen γ sen α ≤ 0 C cos α ≤ 0 tg α ≥ 0 sen δ cos δ cos γ 270º D sen α ≤ 0 cos α ≥ 0 tg α ≤ 0 1 cos 2 α = 1 − 3 8 cos 2 α = 9 8 cos α = − 3 2 tg α = sen α = cos α 1 3 − 8 3 = 1 − 8 =− 8 2 =− 8 4 RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS Ángulos Suplementarios Ángulos que difieren en 180º sen (180º −α ) = sen α 180º– α cos (180º −α ) = − cos α α sen (α + 180º ) = − sen α α+180º α tg (180º −α ) = −tg α cos (α + 180º ) = − cos α tg (α + 180º ) = tg α RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS Ángulos opuestos Ángulos Complementarios sen ( −α ) = − sen α α –α cos ( −α ) = cos α tg ( −α ) = −tg α sen ( 90º −α ) = cos α 90º– α α cos ( 90º −α ) = sen α tg ( 90º −α ) = cotg α RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS Halla las razones trigonométricas del ángulo de 330º. Teorema del seno a 1 sen 330º = sen ( 360º −30º ) = sen ( −30º ) = −sen ( 30º ) = − 2 sen A a = 4 cm Datos: b = 5 cm B = 30º A b 83º 63m 42º a? B a sen A sen A sen C → h B c Ejemplo: Dos lados y el ángulo opuesto. Hallar A = 180º −83º −42º = 55º C c sen C RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA Ejemplo: Dos ángulos y un lado. Hallar a = a b h → h = b ⋅ sen A a b b = b ⋅ sen A = a ⋅ sen B → sen A sen B = h → h = a ⋅ sen B sen B a RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA a c sen A= 1 sen 330º 3 −1 tg 330º = = 2= =− cos 330º 3 3 3 2 C sen B = Demostración: − Datos: b A 3 cos 330º = cos ( 360º −30º ) = cos ( −30º ) = cos ( 30º ) = 2 c = 63 m A = 83º B = 42º = C a 63 sen 83º = → a = 63 ⋅ = 76 ,34 m sen 83º sen 55º sen 55º = b sen B → 4 sen A = A 5cm 5 cm c 30º C 4 cm B 5 4 ⋅ sen 30º → sen A= = 0, 4 sen 30º 5 = 156º 25' 19'' Dos posibles soluciones: A1 = 23º 34' 41'' y A 2 > 180º Si A = 156º 25' 19'' → A+ B A = 23º 34' 41'' RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA Ejemplo: Dos lados y el ángulo que forman. Hallar b Teorema del coseno a = 1200 m Datos: c = 700 m B = 108º a 2 = b 2 + c 2 − 2bc ⋅ cos A b 2 = a 2 + c 2 − 2ac ⋅ cos B c = a + b − 2ab ⋅ cos C 2 RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA 2 2 B 1200m C b C 700m A a b → b = 12002 + 7002 − 2 ⋅1200 ⋅ 700 ⋅ cos 108º b 2 = a 2 + c 2 − 2ac ⋅ cos B b = 1564 ,97 m A 108º c B