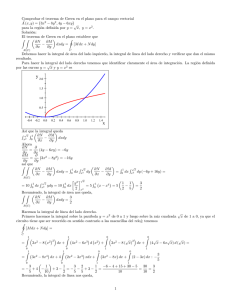
Consideremos la Integral ∫ ∫ dxdy donde R = [0,∞) × [0
Anuncio

Consideremos la Integral
RR
1
dxdy
R (x2 +y 2 )5 +1
donde R = [0, ∞) × [0, ∞) y vamos a comprobar
que es convergente.
Z Z
R
1
dxdy = lı́m
2
n→∞
(x + y 2 )5 + 1
Z
= lı́m
n→∞
π
2
Z
dθ
0
0
n
n
Z
r
dr
10
r +1
Z
0
!
0
n
1
dxdy
2
(x + y 2 )5 + 1
Z
= lı́m
|{z}
n→∞
P olares
0
π
2
Z
0
n
r
drdθ
10
r +1
Z n
Z n
π
r
π
r
= lı́m
dr = lı́m
dr
n→∞
2 0 r10 + 1
2 n→∞ 0 r10 + 1
Esta última integral la vamos a separar de la siguiente manera
Z ∞
Z 1
Z ∞
r
r
r
dr
=
dr
+
dr
10
r10 + 1
r10 + 1
0
0 r +1
1
Para la integral roja definimos f (r) =
r
r 10 +1
la cual esta definida para todo r ∈ [0, 1] y tenemos
que el valor mı́nimo que alcanza f en [0,1] es 0 y para ver el valor máximo de f en [0,1] vamos
a derivar
f (r) =
1 − 9r10
1
r
1
0
⇒
f
(x)
=
⇒ f 0 (x) = 0 ⇔ r = 1 ∴ f ( 1 ) ≈ ·7
10
10
2
r +1
(r + 1)
9 10
9 10
De esta manera tenemos que
r
≤ ·7 ⇒ 0 ≤
0 ≤ 10
r +1
Z
0
1
r10
r
dr ≤ ·7
+1
Por tanto el valor de la integral existe.
Para la integral azul tenemos que
Z n
Z ∞
Z ∞
Z ∞
r
r
1
1
−1
1
dr ≤
dr
dr = lı́m
dr = lı́m 8 |n1 =
10
10
9
9
n→∞
n→∞
r +1
r
r
8r
8
1
1
1 r
1
RR
1
∴ la integral
dxdy converge
R (x2 +y 2 )5 +1
Teorema 1. Criterio de comparación para integrales múltiples de integrando positivo
0 ≤ f (x, y) ≤ g(x, y) ∀(x, y) ∈ D
Z Z
Z Z
g(x, y)dxdy converge ⇒
f (x, y)dxdy converge
Si
D
D
1
!
Demostración. Si In =
RR
Dn
f (x, y)dxdy es una sucesión de números reales entonces es con-
vergente si y solo si es de cauchy, es decir hay que probar que
Dado > 0 ∃ N
tal
que m, n ≥ N ⇒ |Im − In | < Por hipótesis g es convergente entonces la sucesión Jn =
Dado > 0 ∃ N
tal
RR
Dn
g(x, y)dxdy es de cauchy ∴
que m, n ≥ N ⇒ |Jm − Jn | < siendo m ≥ n se cumple Dm ⊃ Dn entonces para cualquier función h (f ó g) se tiene
Z Z
Z Z
Z Z
h(x, y)dxdy =
f (x, y)dxdy +
f (x, y)dxdy
Dm
Dn
h=Dm−Dm
∴
Z Z
Z Z
h(x, y)dxdy −
Z Z
h(x, y)dxdy =
Dm
h(x, y)dxdy
Dn
h=Dm−Dm
Como f ≤ g se tiene que
Z Z
Z Z
f (x, y)dxdy −
Im − In =
Z Z
h=Dm−Dm
Z Z
Z Z
Z Z
g(x, y)dxdy = Jm − Jn < g(x, y)dxdy −
g(x, y)dxdy =
Dn
Dm
h=Dm−Dm
f (x, y)dxdy ≤
f (x, y)dxdy =
Dn
Dm
como h ≥ 0 |Im − In | = Im − In y |Jm − Jn | = Jm − In ∴ |Im − In | ≤ |Jm − Jn | < por lo tanto
In es una sucesión de cauchy ∴ In es convergente
Analogamente se demuetra que
Si 0 ≤ f (x, y) ≤ g(x, y) ∀(x, y) ∈ D
Z Z
Z Z
f (x, y)dxdy diverge ⇒
g(x, y)dxdy diverge
D
D
R R y−x
Aplicando el criterio de comparación comprobar si la integral
en
D (x+y+1)((x2 +y 2 )5 +1) D = [0, ∞) × [0, ∞) converge.
2
Tenemos que
y
−
x
|y| + |x|
|y − x|
(x + y + 1)((x2 + y 2 )5 + 1) ≤ |x + y + 1||(x2 + y 2 )5 + 1| ≤ |x + y + 1||(x2 + y 2 )5 + 1|
≤
∴
Z
0
∞
Z
0
∞
1
(x2 + y 2 )5 + 1
Z
y
−
x
(x + y + 1)((x2 + y 2 )5 + 1) ≤
∞
Z
0
∞
0
((x2
1
dxdy
+ y 2 )5 + 1)
esta última es convergente ∴ la integral pedida es convergente.
Teorema 2. Sea F una función continua de (x,y) en el rectángulo
R = {(x, y) ∈ R2 |a ≤ x ≤ b
y
α ≤ y ≤ β}. Entonces tómese f definido en I : {a ≤ x ≤ b}
por
Z
β
f (x) =
F (x, y)dy
α
es continua en I. Por lo tanto integrable en I, y
Z b
Z β
f (x)dx =
F (x, y)dxdy
a
α
Demostración. Como F es continua en un cerrado y acotado entonces F es uniformemente
continua y
|F (x1 , y) − F (x2 , y)| < si |x1 − x2 | < δ
∴
Z β
Z β
Z β
|f (x1 ) − f (x2 )| = F (x1 , y)dy −
F (x2 , y)dy = F (x1 , y) − F (x2 , y)dy α
α
α
Z β
Z β
≤
|F (x1 , y) − F (x2 , y)| dy <
dy =
(β − α) = (β − α)
α
α (β − α)
si |x1 − x2 | < δ ∴ f es continua
Teorema 3. Sean tanto F como
b
y
∂F (x,y)
∂x
continuas en el rectángulo R = {(x, y) ∈ R2 |a ≤ x ≤
α ≤ y ≤ β}. Entonces f dada por
Z
β
f (x) =
F (x, y)dy
α
3
es diferenciable en I : {a ≤ x ≤ b} y ademas la derivada puede calcularse mediante la diferenciación bajo el signo de integral
d
dx
Z
β
β
Z
F (x, y)dy =
α
α
∂F (x, y)
dy
∂x
Rβ
(x,y)
dy como g es continua
Demostración. Sea g(x) = α ∂F∂x
Z x
Z xZ β
Z βZ x
Z β
∂F (x, y)
∂F (t, y)
g(t)dt =
F (x, y) − F (a, y)dy =
dydt =
dtdy =
∂x
∂t
a
a
α
α
a
α
Z β
Z β
F (x, y)dy −
F (a, y)dy = f (x) − f (y)
α
α
derivando ambos miembros con respecto a x g(x) = f 0 (x) ∴
Z β
∂F (x, y)
0
f (x) =
dy
∂x
α
Ejercicio.-Para cualquier a positiva fija, sea f definida en I : {−a ≤ x ≤ a} por f (x) =
Rβ
α
e−xt dt
a)Demostrar que f es continua en I.
Sol.
R1
e−xt dt y tenemos que:
Z
Z 1
Z 1
e−x1 t dt = |f (x2 ) − f (x1 )| = e−x2 t dt −
Definimos f (x) =
0
0
0
0
Z
0
1
1
Z
e−x2 t − e−x1 t dt ≤
1
−x t
e 2 − e−x1 t dt ≤
0
=
(1 − 0)
En la última desigualdad se utilizo el hecho de que la función e es continua y al considerar un
intervalo cerrado y acotado en este caso [0,1], ahi la función es uniformemente continua
∴ f es continua
b)Evaluar la integral para obtener una fórmula explı́cita para f.
Sol.
Z
0
1
e−xt dt =
−e−xt 1
−e−x −e0
−e−x −e1
=
−
=
+
0
x
x
x
x
x
4
cuya derivada es:
−e−x −e1
+
x
x
0
=
e−x (x + 1)
1
− 2
2
x
x
c) Derivar f mediante la derivación de la integral. Evaluar la integral resultante y verificar que
se obtiene el mismo resultado al derivar la fórmula encontrada en b)
Z 1
Z 1
Z 1
Z 1
∂ −xt
d
−xt
−xt
0
te−xt dt
−te dt = −
e dt =
e dt =
f (x) =
dx
∂x
0
0
0
0
Procediendo por partes tenemos que: u = t, du = dt, dv = e−xt y v =
Z
−
1
−xt
te
0
e−xt
dt = − t
−
−x
Z
0
1
e−xt
−x
por lo tanto
−xt
e−xt
e
1 e−xt 1
e−x e−x
1
dt = − t
+
=
+ 2 − 2
0
−x
−x
x −x
x
x
x
El cual coincide con el resultado de derivar b)
5