MISION INSTITUCIONAL VISION INSTITUCIONAL VALORES
Anuncio
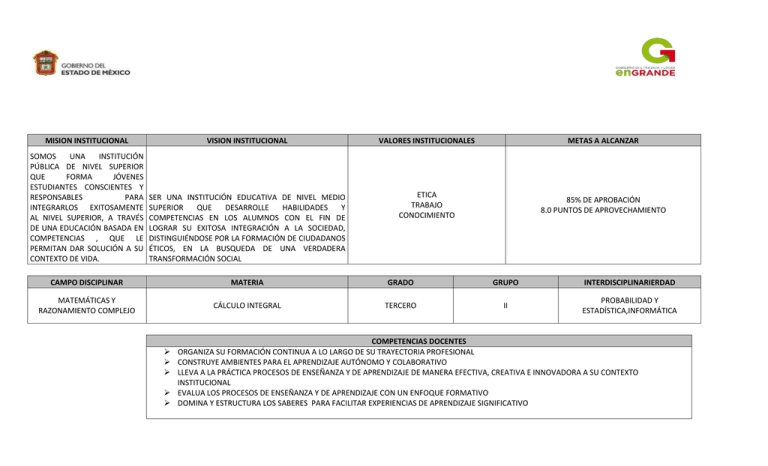
MISION INSTITUCIONAL VISION INSTITUCIONAL VALORES INSTITUCIONALES METAS A ALCANZAR SOMOS UNA INSTITUCIÓN PÚBLICA DE NIVEL SUPERIOR QUE FORMA JÓVENES ESTUDIANTES CONSCIENTES Y RESPONSABLES PARA INTEGRARLOS EXITOSAMENTE AL NIVEL SUPERIOR, A TRAVÉS DE UNA EDUCACIÓN BASADA EN COMPETENCIAS , QUE LE PERMITAN DAR SOLUCIÓN A SU CONTEXTO DE VIDA. SER UNA INSTITUCIÓN EDUCATIVA DE NIVEL MEDIO SUPERIOR QUE DESARROLLE HABILIDADES Y COMPETENCIAS EN LOS ALUMNOS CON EL FIN DE LOGRAR SU EXITOSA INTEGRACIÓN A LA SOCIEDAD, DISTINGUIÉNDOSE POR LA FORMACIÓN DE CIUDADANOS ÉTICOS, EN LA BUSQUEDA DE UNA VERDADERA TRANSFORMACIÓN SOCIAL ETICA TRABAJO CONOCIMIENTO 85% DE APROBACIÓN 8.0 PUNTOS DE APROVECHAMIENTO CAMPO DISCIPLINAR MATERIA GRADO GRUPO INTERDISCIPLINARIERDAD MATEMÁTICAS Y RAZONAMIENTO COMPLEJO CÁLCULO INTEGRAL TERCERO II PROBABILIDAD Y ESTADÍSTICA,INFORMÁTICA COMPETENCIAS DOCENTES ORGANIZA SU FORMACIÓN CONTINUA A LO LARGO DE SU TRAYECTORIA PROFESIONAL CONSTRUYE AMBIENTES PARA EL APRENDIZAJE AUTÓNOMO Y COLABORATIVO LLEVA A LA PRÁCTICA PROCESOS DE ENSEÑANZA Y DE APRENDIZAJE DE MANERA EFECTIVA, CREATIVA E INNOVADORA A SU CONTEXTO INSTITUCIONAL EVALUA LOS PROCESOS DE ENSEÑANZA Y DE APRENDIZAJE CON UN ENFOQUE FORMATIVO DOMINA Y ESTRUCTURA LOS SABERES PARA FACILITAR EXPERIENCIAS DE APRENDIZAJE SIGNIFICATIVO UNI DA D MACRO RETÍCUL A MESO RETÍCULA MICRO RETÍCULA 1.1.1 Situaciones de áreas de figuras en forma numérica y algebraica COMPETENCIAS CATEG ORÍA Se expresa y se comunica Piensa crítica y reflexiva mente I LA INTEGRA L 1.1 Construcci ón del área bajo la curva 1.1.2 Aproximación del área bajo la curva por extremos derechos e izquierdos a partir de situaciones contextuales 1.1.3 Solución de situaciones de distancia a partir de la velocidad como área bajo la curva 2.1.1 La integral definida como límite de una sumatoria de áreas II SIGNIFICA DO DE LA INTEGRA L DEFINIDA 2.1 Significado de la integral definida 2.1.2 Cálculo de integrales definidas con sumatorias de Riemman 2.1.3 El teorema del punto medio Aprende en forma autónom a Trabaja en forma colaborat iva GENERI CA Argument a la solución la obtenida de un problema sobre áreas con métodos numéricos , gráficos y analíticos o variacional es mediante el lenguaje verbal matemátic o y el uso de las tecnología s de la informació n y la comunicac ión Explica e interpreta los resultados obtenidos mediante procedimien tos matemático s y los contrasta con modelos establecido so situaciones reales ATRIBUTO ACTIVIDADES BÁSICAS EXTENDIDAS Calcula áreas de figuras regulares principalmente rectangulares y con lados curvos utilizando procedimientos numéricos y algebraicos Escucha, interpreta y emite mensajes pertinentes en distintos contextos mediante la utilización de medios, códigos y herramientas apropiadas Desarrolla innovaciones y propone soluciones a problemas a partir de métodos establecidos Sustenta una postura personal sobre temas de interés y relevancia general, considerando otros puntos de vista de manera crítica y reflexiva Aprende por iniciativa propia a lo largo de la vida Visualiza y obtiene en forma aproximada el área de la región limitada por una curva y el eje x en el plano utilizando procedimientos numéricos Construye e interpreta modelos matemáticos mediante la aplicación de modelos aritméticos, algebraicos, geométricos y variacionales para la comprensión y análisis de situaciones reales, hipotéticas o formales Resuelve situaciones contextuales que originan calcular el área bajo una curva, por ejemplo la distancia a partir de la velocidad de un móvil Identifica la integral definida como límite de una suma bajo la curva a partir de situación es contextuales Identifica y utiliza las sumas de Riemman para evaluar el área bajo una curva emanada de situaciones contextuales relacionadas con las ciencias sociales o naturales Visualiza y utiliza el teorema del punto medio como un procedimiento que permite evaluar una integral definida en la solución de situaciones contextuales Planteamiento de interrogantes que plantean una serie de dudas en base a un problema contextual cuyo escenario es el Gran Premio de la Fórmula 1 Investigación sobre el origen del Cálculo Integral Investigación sobre el método de exhaución de Arquimides Investigación del cálculo de áreas bajo una curva utilizando rectángulos izquierdos y derechos Presentación en forma colaborativa de la solución al problema planteado mediante el uso de las tecnologías Argumentación de la solución del problema por cada equipo Resolución de ejercicios contextuales sobre el cálculo de áreas bajo la curva Planteamiento de interrogantes que plantean una serie de dudas en base a un problema contextual emanado de las ciencias sociales o naturales Investigación sobre las propiedades de las sumatorias Explicación sobre el uso de las sumatorias de Riemman Resolución de ejercicios contextuales sobre el cálculo de áreas bajo la curva y el teorema del punto medio utilizando el método de Sumatorias de Riemman EVALU ACIÓN RÚBRI CAS FECHAS 28/01 al8/02 del 2013 15%Tra 11/02 bajo al18/02 Power de 2013 point 15% Ejercici os de clase 19/02 al 26/03 de 2013 10% Evalua 27/02 al ciones 6/03 de parciale 2013 s 8/03 al 15/03 de 2013 19/03 al 10/04 de 2013 COMPETENCIAS UNI DAD MACR O RETÍC ULA MESO RETÍCUL A MICRO RETÍCULA 3.1.1. Teorema fundamental del cálculo 3.1 Teorema fundament al del cálculo 3.1.2. La derivada y la integral como procesos inversos 3.2.1. La integral indefinida como una familia de funciones en forma geométrica y algebraica III LA INTEG RAL INDEFI NIDA 3.2 La integral indefinida en situaciones contextual es 3.2.2.Fórmulas básicas de integración con problemas contextuales 3.2.3. La regla de sustitución con problemas contextuales CATE GORÍ A GENÉRIC A ATRIBUTO Identificar el teorema del cálculo para hallar la primitiva de una función Se expres a y se comun ica Piensa crítica y reflexiv ament e Apren de en forma autóno ma Trabaj a en forma colabo rativa ACTIVIDADES BÁSICAS Compren de y aplica el proceso de la integral indefinida para hallar la primitiva de una función en la solución de situacione s contextual es Escucha, interpreta y emite mensajes pertinentes en distintos contextos mediante la utilización de medios, códigos y herramientas apropiadas Aprende por iniciativa propia a lo largo de la vida Identifica el teorema fundamental del cálculo y sus implicaciones con la integral definida Establece a partir del Teorema fundamental del cálculo la derivación y la integración como procesos inversos Identifica la integral indefinida como el proceso para hllar la primitiva de una función Desarrolla innovaciones y propone soluciones a problemas a partir de métodos establecidos Sustenta una postura personal sobre temas de interés y relevancia general, considerando otros puntos de vista de manera crítica y reflexiva EXTENDIDAS La integral indefinida en situaciones contextuales Utiliza las fórmulas básicas de integración para resolver e interpretar situaciones contextuales Utiliza la regla de sustitución para plantear, resolver e interpretar situaciones contextuales EVALUA CIÓN RÚBRIC AS FECHAS Construir el concepto de función primitiva con base en la lectura realizada y el vídeo consultado, discutirlo en ternas y desarrollarlo en un organizador grafico socializarlo para exponerlo al grupo. 12/04 al 19/04 de 2013 Analizar e interpretar a la función primitiva como la antiderivada de una función, su notación y al Cálculo Integral como el proceso inverso del Cálculo Diferencial en problemas de ciencias exactas (área bajo una curva), naturales (crecimientos exponenciales) y sociales (oferta y demanda), manifestando su opinión escrita mediante una reflexión, después de resolver los ejercicios propuestos. 22/04 al 26/04 de 2013 Resolver ejercicios de manera individual sobre integrales inmediatas y técnicas de integración para adquirir habilidad operativa en un contexto teórico, comentar al grupo los obstáculos que encontraron al integrar funciones y dar sugerencias para identificar correctamente el tipo de técnica a aplicar de acuerdo a la forma de la función. 10%Car peta de evidenci as 15% Ejercicio s de clase 15% Evaluaci ones parciales 29/04 al 14/05 de 2013 17/05 al 24/05 de 2013 27/05 al 31/05 de 2013 COMPETENCIAS NI DAD MACR O RETÍC ULA MESO RETÍCUL A MICRO RETÍCULA 4.1.1. Integración por partes IV TECNI CAS DE INTEG RACIÓ N EN SITUA CIONE S CONT EXTUA LES 4.1.2. Integrales trigonométricas 4.1 Técnicas de integración 4.1.3. Integrales por sustitución trigonométrica 4.1.4. Integrales de funciones racionales por fracciones parciales CATE GORÍ A Se expres a y se comun ica Piensa crítica y reflexiv ament e Apren de en forma autóno ma Trabaj a en forma colabo rativa GENÉRIC A Explica e interpreta los resultado s obtenida de situacione s contextual es reales o hipotética s a través del uso de técnicas de integració n ATRIBUTO ACTIVIDADES BÁSICAS EXTENDIDAS EVALUA CIÓN RÚBRIC AS 3/06 al 7/06 de 2013 Utiliza la integración por partes para plantear, resolver situaciones contextuales Escucha, interpreta y emite mensajes pertinentes en distintos contextos mediante la utilización de medios, códigos y herramientas apropiadas Desarrolla innovaciones y propone soluciones a problemas a partir de métodos establecidos Sustenta una postura personal sobre temas de interés y relevancia general, considerando otros puntos de vista de manera crítica y reflexiva Resuelve integrales trigonométricas utilizando los criterios adecuados para su solución Analiza y resuelve problemas en contexto, aplicando métodos de integración Utiliza la integración por sustitución trigonométrica para plantear, resolver situaciones contextuales FECHAS Analiza y resuelve problemas contextuales de manera individual que utilicen las diferentes técnicas de integración Presentación en ternas de un problema contextual que utilice los métodos de integración Aprende por iniciativa propia a lo largo de la vida 10%Car peta de evidenci as 10/06 al 14/06 de 2013 15% Ejercicio s de clase 15% Evaluaci ones parciales Utiliza la integración por fracciones parciales para plantear, resolver situaciones contextuales CATEDRÁTICO DE LA MATERIA Vo. Bo. DE LA SUBDIRECTORA ACADÉMICA PROFR. ALFREDO SALGADO VARÓN MTRA. ANA GABRIELA FERNÁNDEZ JIMÉNEZ _____________________________________________________________________ ____________________________________________________________________ 17/06 al 21/06 de 2013 24/06 al 4/07 de 2013
