taller de recuperación de química 8 grado j. tarde
Anuncio

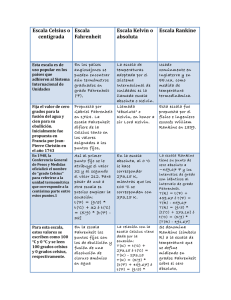
I.E. INTEGRADO DE SOACHA TALLER DE RECUOERACION QUIMICA GRADO 8 J.TARDE 2015 Doc. Hugo Cortes LA TEMPERATURA Se puede definir la temperatura como la propiedad de un cuerpo que determina la dirección del flujo de calor. Esto significa que dos cuerpos a la misma temperatura puestos en contacto entre sí no efectúan una transferencia de calor. Por otra parte, si se ponen en contacto dos cuerpos con temperaturas distintas, el calor fluye del más caliente al más frío. La unidad SI de temperatura es el kelvin; 1 kelvin (K) se define como 1/273.16 veces la temperatura del punto triple del agua. El punto triple es la temperatura a la que el agua líquida se encuentra en equilibrio con el hielo (agua sólida) a la presión ejercida sólo por el vapor de agua. La mayoría de las personas están más familiarizadas con el punto de congelación normal del agua (273.15 K), que sólo es 0.01 K menor que el punto triple del agua. El punto de congelación normal del agua es la temperatura a la que coexisten el agua y el hielo en equilibrio con aire a presión atmosférica normal (1 atm). La unidad en el SI de temperatura se define de forma que 0 K es la temperatura del cero absoluto. La escala SI o Kelvin se denomina con frecuencia escala de temperatura absoluta. Aunque parece que no se puede alcanzar el cero absoluto, se ha aproximado a menos de 10−4 K. OTRAS ESCALAS DE TEMPERATURA En la escala Celsius de uso común (nombre tradicional: escala centígrada), una diferencia de temperatura de un grado es igual que un grado en la escala Kelvin. El punto de ebullición normal del agua es 100°C; su punto de congelación normal, 0°C, y el cero absoluto es −273.15°C. Una diferencia de un grado en la escala Fahrenheit equivale exactamente a 5/9 K. El punto de ebullición normal del agua es 212°F; su punto de congelación normal, 32°F, y el cero absoluto es −459.67°F. En la figura 1-1 se ilustra la relación entre las tres escalas. La conversión de una escala a otra se hace con las ecuaciones que se muestran a continuación. Las ecuaciones de la derecha representan una reorganización de las ecuaciones de la izquierda. No es necesario memorizar dos ecuaciones que se utilizan para el mismo cálculo: es suficiente aprenderse una de ellas, sustituir los valores y despejar la incógnita. K = °C + 273.15 °F = °C + 32 o o °C = K – 273.15 °C = (°F – 32) USO CORRECTO E INCORRECTO DE LAS UNIDADES Debe tenerse en cuenta que las cantidades no pueden sumarse ni restarse directamente a menos que tengan no sólo las mismas dimensiones, sino también las mismas unidades. Además, las unidades se pueden simplificar durante las operaciones de multiplicación o división. Las unidades del resultado deben coincidir con la naturaleza de la dimensión (por ejemplo, la longitud no se puede expresar en gramos). No es posible sumar 5 horas (tiempo) con 20 millas/hora (velocidad), debido a que tiempo y velocidad tienen distinto significado físico. Si se tiene que sumar 2 lb (masa) y 4 kg (masa), primero se deben convertir lb a kg o kg a lb. Sin embargo, se pueden combinar cantidades de diversos tipos en las multiplicaciones o divisiones, ya que las unidades, al igual que los números se apegan a las leyes algebraicas de multiplicación, elevación al cuadrado, división y simplificación. Es importante recordar estos conceptos: 1. 6 L + 2L = 8L 2. (5 cm) x (2 cm2) = 10 cm3 3. (3 pie3) x (200 lb. /pie3) = 600 lb. 4. (2 s) x (3 m/s2) = 6 m/s 5. MÉTODO DEL FACTOR UNITARIO O FACTORES DE CONVERSIÓN Una forma de resolver problemas consiste en analizar las unidades, esta técnica se denomina método del factor unitario o análisis dimensional. En esencia, la resolución de un problema se logra al convertir la o las unidades de los datos del problema a la o las unidades finales que se desean, mediante la multiplicación por una fracción llamada factor unitario o tan sólo factor. El numerador y el denominador del factor deben representar la misma cantidad (mL/mL, pie/pie, y no mL/L, pie/pulg). EJEMPLO 5 Convierta 5.00 pulgadas a centímetros. El factor unitario adecuado es 2.54 cm/1 pulg. El resultado de este problema se obtiene al multiplicar el valor problema de 5.00 pulgadas por el factor, de manera que se simplifiquen las dimensiones. 5.00 pulg × 2.54 cm / 1 pulg = 12.7 cm Observe que se simplifican las pulgadas (pulg) y sólo se obtienen centímetros (cm). EJEMPLO 6 ¿Cuál es el peso, en gramos, de siete clavos tomados de un lote de clavos que pesa 0.765 kg por gruesa? La simplificación de las unidades ayuda a la resolución del problema. La resolución contiene un factor unitario de dimensiones mixtas (0.765 kg/1 gruesa de clavos). El factor unitario no está compuesto de medidas universalmente equivalentes, porque una gruesa de distintas clases de clavos tiene diferente peso. Habrá muchos ejemplos parecidos durante todos sus cursos. ESTIMACIÓN DE LOS RESULTADOS NUMÉRICOS Cuando se resuelven problemas suponemos que la calculadora funciona bien, que todos los números se introdujeron en ella y se teclearon en forma correcta. Suponga que una o más de estas consideraciones son incorrectas, ¿se aceptará tal resultado? Una destreza importante es determinar, por inspección visual, un resultado aproximado. Tiene especial importancia el orden de magnitud correcto, representado por el lugar del punto decimal puede (o por la potencia de 10). PROBLEMAS RESUELTOS UNIDADES BASADAS EN MASA O LONGITUD 1.1. En los siguientes ejemplos se ilustran conversiones entre diversas unidades de longitud, volumen o masa: 1 pulgada = 2.54 cm = 0.0254 m = 25.4 mm = 2.54 × 107 no 1 pie = 12 pulg = 12 pulg × 2.54 cm/pulg = 30.48 cm = 0.3048 m = 304.8 mm 1 litro = 1 dm3 = 10−3 m3 1 milla = 5 280 pies = 1.609 × 105 cm = 1.609 × 103 m = 1.609 km = 1.609 × 106 mm 1 libra = 0.4536 kg = 453.6 g = 4.536 × 105 mg 1 ton métrica = 1 000 kg = 106 g (o bien, 1 × 106 g) Ejercicios de TEMPERATURA El alcohol etílico a) hierve a 78.5°C y se congela a −117°C, a una atmósfera de presión. Convierta estas temperaturas a la escala Fahrenheit. Utilice la siguiente conversión: o F= + 32; a) ( b) ( o C) + 32 = 173 oF o C) + 32 = 179 oF El mercurio a) hierve a 675°F y b) se solidifica a −38.0°F, a una atmósfera de presión. Exprese estas temperaturas en grados Celsius. Use la siguiente conversión o C= ( oF -32) a) ( 675 – 32 ) = 357 oC b) = ( -38.0 -32) = -38.9 oC Pase a) 40 o C y - 5 o C a grados Kelvin use el siguiente factor de conversión o C+ 273 = oK a) 40 oC+ 273 = 313 oK b) - 5 oC+ 273 = 313 oK Conviertan a) 220 oK y 498 oK a la escala Celsius. Usen la siguiente conversión: oK – 273 = oC a) 220 oK -273 = -53 oC b) 498 oK -273 = 225 oC Durante un experimento, la temperatura en el laboratorio aumento 0.8 oC, exprese el aumento en grados Fahrenheit. Ver la figura de los termómetros, en la Kelvin hay 180 divisiones del punto de licuefacción al punto de ebullición del agua y en la Celsius hay 100, por lo que por cada 5 grados en la Celsius hay 9 en la Fahrenheit Se debe deducir que hay que conseguir un número que divida a 100 y a 180 o sea que haya un número entero y ese es 20 entonces: 100 / 20 = 5 y 180 / 20 = 9 para pasar de Celsius a Fahrenheit se usa 9/5 y al contrario de Fahrenheit a Celsius 5/9 como factores. 100 oC 180 oF por lo tanto ( ) x (0.8 oC) = 1.4 oF EJERCICIOS DE TEMPERATURA a) Convierta 88°F a °C; 16°F a °C; 130°F a °C. b) Convierta 35°C a °F; 2°C a °F; −29°C a °F. Resp. a) 31°C, –9°C, 54°C; b) 95°F, 36°F, –20°F Convierta las siguientes temperaturas: −149.7°C a °F; −396.0°F a °C; 1 555°C a °F. Resp. −237.5°F, −237.8°C, 2 831°F La temperatura del hielo seco (temperatura de sublimación a la presión normal) es −109°F. ¿Es mayor o menor que la temperatura de ebullición del etano (un componente del gas embotellado), que es −88°C? Resp. mayor Una persona enferma tiene 103°F de temperatura, más o menos la misma temperatura que un gato sano. ¿Cuál es esa temperatura en: a) °C y b) kelvins? Resp. a) 39.4°C; b) 312.6 K Se ha extraído y refinado oro durante muchos miles de años, antes de que hubiera hornos eléctricos y otros aparatos de alta temperatura. El punto de fusión del oro es 1 064°C; exprese esa temperatura en las escalas Kelvin y Fahrenheit. Resp. 1 303 K y 1 947°F Los metales se contraen y dilatan cuando cambia la temperatura. Se utiliza una barra de metal para construir parte de la plataforma de una torre petrolera para el Mar del Norte, que debe resistir −45°C. Indique la temperatura en a) °F y b) en la escala Kelvin. Resp. a) −49°F; b) 228 K En 1714, Gabriel Fahrenheit sugirió que el punto cero en su escala fuera la temperatura mínima obtenible con una mezcla de sales y hielo, y como punto 100°F la temperatura normal máxima conocida en algún animal. Exprese esos “extremos” en grados Celsius. Resp. −17.8°C, 37.8°C El sodio metálico tiene un intervalo muy grande de temperaturas en estado líquido; funde a 98°C y hierve a 892°C. Exprese el intervalo del estado líquido en grados Celsius, kelvins y Fahrenheit. Resp. 794°C, 794 K, 1 429°F Convierta 298 K, 892 K y 163 K en grados Celsius. Resp. 25°C, 619°C, −110°C Exprese 11 K y 298 K en grados Fahrenheit. Resp. −440°F, 77°F Convierta 23°F en grados Celsius y en kelvins. Resp. −5°C, 268 K Durante el incendio de un vehículo se puede alcanzar una temperatura tan alta que se funde el vidrio del parabrisas. El punto de fusión de ese vidrio de automóvil (en esencia, SiO2) es 1 698°C. Convierta esa temperatura a: a) la escala Kelvin, y b) la escala Fahrenheit. Resp. a) 1 971 K; b) 3 088°F ¿A qué temperatura las lecturas en grados Celsius y Fahrenheit tienen el mismo valor numérico? Resp. −40° La temperatura corporal normal es 98.6°F, pero la temperatura interna (del hígado) de una persona fallecida que se encontró en un apartamento fue 91.5°F. La disminución de la temperatura esperada en las condiciones del apartamento es de 1°C por cada hora y 15 min después del deceso. a) Exprese la temperatura corporal en °C. b) ¿Cuánto tiempo hace que falleció esa persona? (Con estos datos y la rapidez de enfriamiento sólo se puede obtener una estimación.) Resp. a) 37°C y 33°C; b) 6 horas, aproximadamente Actividad Resuelva los ejercicios propuestos y entregarlos en hojas al inicio de las clases, después de vacaciones Fuente: QUÍMICA, Serie Schaum Novena edición