TEMA 9: ESTADÍSTICA CONCEPTOS BÁSICOS Población. Es el

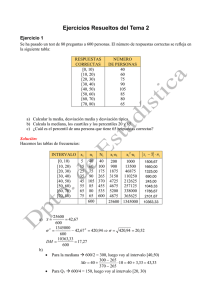
TEMA 9: ESTADÍSTICA
CONCEPTOS BÁSICOS
Población. Es el conjunto de todos los elementos cuyo conocimiento nos interesa y que serían objeto de nuestro estudio.
Muestra es un subconjunto extraído de la población, cuyo estudio sirve para inferir características de toda la población.
Individuo es cada uno de los elementos que forman la población o la muestra.
Caracteres son los aspectos que deseamos estudiar en los individuos de una población. Los valores que damos a los
caracteres se llaman variables y estas pueden ser de dos tipos:
- Variable cuantitativa si toman valores numéricos. Estas a su vez se dividen en dos tipos:
 Discretas si solo toman valores aislados. Por ejemplo ……
 Continuas si pueden tomar cualquier valor de un intervalo. Por ejemplo ……
- Variable cualitativa si toman valores no numéricos. Por ejemplo …..
LAS DOS RAMAS DE LA ESTADÍSTICA
La estadística descriptiva trata de describir y analizar algunos caracteres de los individuos de un grupo dado
(población) sin extraer conclusiones para un grupo mayor.
Por ejemplo si hacemos un estudio sobre los resultados académicos de los alumnos de 4º eso de nuestro colegio para
compararlos con otros estudios de años anteriores sería estadística descriptiva, pues se realiza sobre la totalidad de la
población.
La estadística inferencial trabaja con muestras y pretende, a partir de ellas, ―inferir‖ características de toda la población.
Es decir, se pretende tomar como generales propiedades que solo se han verificado para casos particulares. En este proceso
hay que operar con mucha cautela: ¿Cómo se elige la muestra? ¿Qué grado de confianza se puede tener en el resultado
obtenido?
Por ejemplo se realiza una encuesta 400 alumnos de una universidad sobre sus preferencias en la lectura, con el fin de
extraer consecuencias válidas para todos los universitarios. Esto es estadística inferencial, pues , a partir de una muestra,
se desea obtener información de toda la población.
TABLAS DE FRECUENCIA
Una vez recogidos los datos estos se agrupan en tablas de frecuencia.
Cuando los valores que toma la variable son pocos se colocan los valores en una columna (xi) y a su lado las veces que se
repite cada dato (fi)
Cuando el número de valores que toma la variable es grande, conviene elaborar una tabla de frecuencias agrupándolos en
intervalos. Para ello vamos a ver un ejemplo.
En una maternidad se han tomado los pesos (en kilogramos) de 50 recién nacidos:
2,8 3,2 3,8 2,5 2,7 3,7 1,9 2,6 3,5 2,3
3,0 2,6 1,8 3,3 2,9 2,1 3,4 2,8 3,1 3,9
2,9 3,5 3,0 3,1 2,2 3,4 2,5 1,9 3,0 2,9
2,4 3,4 2,0 2,6 3,1 2,3 3,5 2,9 3,0 2,7
2,9 2,8 2,7 3,1 3,0 3,1 2,8 2,6 2,9 3,3
Localizamos los valores extremos, que son ……. y ……. , y calculamos el recorrido que es su diferencia
r=
Decidimos el número de intervalos que vamos a tomar (entre 6 y 15), y según el número calculamos la longitud de cada
intervalo (ha de ser igual para todos)
Nosotros tomaremos …… intervalos. Empezaremos por un número algo menor que el extremo menor y terminaremos
en un número algo mayor que el extremo mayor. Y ahora viene lo peor, hemos de contar cuántos datos hay en cada
intervalo.
El punto medio de cada intervalo se llama marca de clase, y es el valor que utilizaremos para futuros cálculos.
PARÁMETROS ESTADÍSTICOS
A partir de una tabla de frecuencia veremos cómo se obtienen los parámetros
Media aritmética: x 
x  f
f
i
i
. Para calcular éste parámetro añadimos una nueva columna
i
Desviación típica:  
x  f
f
2
i
i
i
2
 x . Para calcular éste parámetro añadimos una nueva columna
Coeficiente de variación. Sirve para comparar las dispersiones de poblaciones heterogéneas, pues indica la variación
relativa. C.V . 

x
En nuestro ejemplo el C.V. =
Ejercicio.
1. Calcula los anteriores parámetros en la siguiente distribución
MEDIDAS DE POSICIÓN
Mediana. Es el valor que queda en medio si colocamos los valores en orden creciente. Se representa Me y por encima de
ella está el 50% de la población y por debajo, el otro 50%. Si el número de valores es par se toma como mediana la media
de los dos valores centrales.
Por ejemplo:
6 , 7 , 7, 7 , 8 , 9 , 10 , 12 , 15 la mediana será Me =
6 , 7 , 7, 7 , 8 , 9 , 10 , 12 , 15 , 16 La mediana será Me=
Cuartiles. Si en lugar de dividir los valores en dos mitades, lo hacemos en cuatro partes iguales, los nuevos puntos de
separación se llaman cuartiles.
Q1 es el cuartil inferior y tiene por debajo el 25% de la población y por encima, el 75%
Q2 es la mediana
Q3 es el cuartil superior t tiene por debajo el 75% de la población y por encima, el 25%
Por ejemplo en la distribución 1 , 2 , 2 , 3 , 4 , 5, 5 , 5 , 6 , 8 , 9 , 10 los cuartiles serán:
Q1 =
Q2 = Me =
Q3 =
Percentiles. Si partimos la población en 100 partes y señalamos el lugar que deja debajo k de ellas, el valor
correspondiente a ese lugar se designa pk y se denomina percentil k.
La mediana es Me = p50, y los cuartiles, Q1 = ……, Q3 = …..
Ejercicio.
2. Calcula Me, Q1, Q3, p10 y p80 en la distribución:
1 , 1 , 2 , 3 , 4 , 4, 5 , 5 , 5 , 5 , 6 , 7 , 7 , 7 , 8 , 9 , 10
Frecuencias acumuladas. Cuando las distribuciones están dadas por tablas de frecuencias acudimos al concepto de
frecuencia acumulada para facilitar los cálculos.
Veamos un ejemplo.
El percentil pk es el valor para el cual la frecuencia
acumulada correspondiente supera el k%.
En el caso de que una de ellas coincida con k%, se
toma como pk el valor intermedio entre ese valor de xi
y el siguiente
Q1 =
P73 =
Q2 = Me =
Q3 =
P85 =
Ejercicio.
3. En la fabricación de cierto tipo de bombillas se han detectado algunas defectuosas. Se han estudiado 200 cajas de 100
bombillas cada una, obteniéndose la siguiente tabla:
Calcula la mediana, los cuartiles y los percentiles p10, p90 y p95.
DIAGRAMAS DE CAJA
El diagrama de caja (también llamado de caja y bigotes) son una forma de representar las distribuciones estadísticas.
La caja abarca el intervalo Q1 , Q3 y en ella se señala el valor de la mediana, Me.
Los bigotes se trazan hasta abarcar la totalidad de los individuos, con la condición de que cada largo no supere 1,5 veces
la longitud de la caja.
Si uno o más valores queda por debajo o por encima de esa longitud, el correspondiente bigote se dibujaría con esa
limitación y se señalarían los individuos que quedaran fuera mediante un asterisco (serían valores atípicos)
Ejercicios.
4. Interpreta el siguiente diagrama de caja. En él se representan las alturas de un grupo de personas.
Todos miden entre ……. cm y ….. cm, excepto uno que mide …… cm.
Un 25% de las personas miden menos de …..
Un 25% mide entre ……. cm y …… cm
Un 25% mide entre ……. cm y ……. cm
Un 25% mide más de ….. cm.
5. Haz el diagrama de caja correspondiente a esta distribución
ESTADÍSTICA INFERENCIAL
Esta rama de la estadística trabaja con muestras, y del estudio de ésta, se infieren conclusiones para toda la población.
Las causas para elegir una muestra pueden ser los siguientes:
- La población es excesivamente numerosa.
- La población es difícil o imposible de controlar.
- El proceso de medición es destructivo o demasiado caro.
- Se desea conocer rápidamente los resultados y se tardaría demasiado tiempo en realizar las mediciones.
El tamaño de la muestra no tiene que ser pequeño y ésta se ha de elegir al azar, de este modo todos los individuos de la
población tienen la misma probabilidad de ser elegidos.
Ejercicio.
6. Se desea conocer el número de horas que dedican al estudio los 1000 alumnos de un colegio, para ello se extrae una
muestra de 100 de ellos. Reflexiona sobre la validez de cada uno de los métodos seguidos para escoger la muestra.
a) El director los elige procurando que haya alumnos de todo tipo.
b) Se eligen los 100 primeros que lleguen al colegio un cierto día
c) Se numeran del 1 al 1000 y se eligen al azar 100 de ellos.
EJERCICIOS
1. El número de faltas de ortografía que cometieron un grupo de estudiantes en un dictado fue:
03120
21304
01143
53241
50210
00021
21003
05321
a) Di cuál es la variable y de qué tipo es.
b) Haz una tabla de frecuencias y representa los datos en un diagrama adecuado.
2. Las urgencias atendidas durante un mes en un centro de salud fueron:
15321
64223
43510
15336
24632
43215
a) ¿Cuál es la variable y de qué tipo es?
b) Haz una tabla de frecuencias y representa los datos.
3. En una maternidad se han tomado los pesos (en kilogramos) de 50 recién nacidos:
2,8 3,2 3,8 2,5 2,7
3,0 2,6 1,8 3,3 2,9
2,9 3,5 3,0 3,1 2,2
2,4 3,4 2,0 2,6 3,1
2,9 2,8 2,7 3,1 3,0
3,7 1,9 2,6 3,5 2,3
2,1 3,4 2,8 3,1 3,9
3,4 2,5 1,9 3,0 2,9
2,3 3,5 2,9 3,0 2,7
3,1 2,8 2,6 2,9 3,3
a) ¿Cuál es la variable y de qué tipo es?
b) Construye una tabla con los datos agrupados en 6 intervalos de 1,65 a 4,05.
c) Representa gráficamente esta distribución.
4. A un grupo de 30 personas se les ha tomado el número de pulsaciones por minuto (ritmo cardíaco) obteniéndose los
siguientes resultados:
87 85 61 51 64 75 80 70 69 82
80 79 82 74 92 76 72 73 63 65
67 71 88 76 68 73 70 76 71 86
Representa gráficamente esta distribución agrupando los datos en 6 intervalos (desde 50,5 a 92,5).
5. Deseamos hacer una tabla con datos agrupados a partir de 384 datos, cuyos valores extremos son 19 y 187.
a) Si queremos que sean 10 intervalos de amplitud 17, ¿cuáles serán esos intervalos?
b) Haz otra distribución en 12 intervalos de la amplitud que creas conveniente.
6. Halla la media, la desviación típica y el coeficiente de variación en las siguientes distribuciones:
a)
b)
c)
d)
Sol: a) x = 1,7 σ = 1,57 CV = 0,9235 b) x = 3,1 σ = 1,59 CV = 0,5129
c) x = 2,9 σ = 0,39 CV = 0,1345 d) x = 74,3 σ = 9,1 CV = 0,1225.
7. Los gastos mensuales de una empresa A tienen una media de 100 000 euros y una desviación típica de 12 500 euros.
En otra empresa B la media es 15 000 euros, y la desviación típica, 2 500 euros. Calcula el coeficiente de variación y
di cuál de las dos tiene más variación relativa. Sol: Tiene mayor variación relativa la empresa B.
8. El peso medio de los alumnos de una clase es de 58,2 kg, y su desviación típica, 3,1 kg. El de las alumnas de esa
clase es 52,4 kg y su desviación típica es 5,2 kg. Calcula el coeficiente de variación y compara la dispersión de
ambos grupos. Sol: El peso medio de las alumnas es más variable que el peso de los alumnos.
9. Se han pedidos los pesos y las alturas de 6 personas, obteniéndose los siguientes datos:
Calcula el coeficiente de variación y di si están más dispersos los pesos o las alturas.
Sol: Están más dispersas las alturas que los pesos.
10. La mediana y los cuartiles de la distribución de ―Aptitud para la música‖ (escala 1-100) en un colectivo de personas
son Q1 = 31, Me = 46 y Q3 = 67.
Completa las siguientes afirmaciones:
a) El 75% tiene una aptitud superior o igual a ——.
b) El 25% tiene una aptitud superior o igual a ——.
c) El ——% tiene una aptitud igual o menor a 46 puntos.
d) El ——% tiene una aptitud superior o igual a 46 e inferior o igual a 67.
e) El ——% tiene una aptitud superior o igual a 31 e inferior o igual a 67.
11. La altura, en centímetros, de un grupo de alumnos y alumnas de una misma clase es:
150 169 171 172 172 175 181
182 183 177 179 176 184 158
Calcula la mediana y los cuartiles y explica el significado de estos parámetros.
Sol: Me = 175,5 cm; Q1 = 171 cm (4.° lugar); Q3 = 181 cm (posición 11).
12. Calcula la mediana y los cuartiles de la siguiente distribución:
Sol: Me = 1, Q1 = 0 y Q3 = 3.
13. Halla la mediana, los cuartiles y el percentil 60 en cada una de las siguientes distribuciones, correspondientes a las
notas obtenidas en un test que han hecho dos grupos de estudiantes:
A: 25 – 22 – 27 – 30 – 23 – 22 – 31 – 18 - 24 – 25 – 32 – 35 – 20 – 28 – 30
B: 27 – 32 – 19 – 22 – 25 – 30 – 21 - 29 – 23 – 31 – 21 – 20 – 18 – 27
Sol: A: Me = 25, Q1 = 22 (4ª posición), Q3 = 30 (12ª posición) y p60 = 27,5 (entre 9ª y 10ª posición)
B: Me = 24, Q1 = 21 (4ª posición), Q3 = 29 (11ª posición) y Q3 = 29 (11ª posición)
14. En la fabricación de cierto tipo de bombillas se han detectado algunas defectuosas. Se han estudiado 200 cajas de
100 bombillas cada una, obteniéndose la siguiente tabla:
Calcula la mediana, los cuartiles y los percentiles p10, p90 y p95.
Sol: Q1 = p25 = 3 , Q3 = p75 = 6 , p10 = 2,5 , p90 = 6,5 , p95 = 7
15. Las puntuaciones obtenidas por 87 personas tienen los siguientes parámetros de posición:
Q1 = 4,1; Me = 5,1 y Q3 = 6,8. Todas las puntuaciones están en el intervalo 1 a 9. Haz el diagrama de caja.
16. Las estaturas de 35 alumnos de una clase están comprendidas entre 153 y 188. Los tres restantes miden 151, 152
y 190. Conocemos los siguientes parámetros: Q1 = 161; Me = 166 y Q3 = 176.
Haz un diagrama de caja para esta distribución.
17. Se quiere realizar los siguientes estudios:
III. Tipo de transporte que utilizan los vecinos de un barrio para acudir a su trabajo.
III. Estudios que piensan seguir los alumnos y alumnas de un centro escolar al terminar la ESO.
III. Edad de las personas que han visto una obra de teatro en una ciudad.
IV. Número de horas diarias que ven la televisión los niños y niñas de tu comunidad autónoma con edades
comprendidas entre 5 y 10 años.
a) Di en cada uno de estos casos cuál es la población.
b) ¿En cuáles de ellos es necesario recurrir a una muestra? ¿Por qué?
18. ¿Cómo se puede contar el número aproximado de palabras que tiene un cierto libro?
— Se seleccionan, abriendo al azar, unas cuantas páginas y se cuentan las palabras en cada una.
— Se calcula el número medio de palabras por página.
— Se da un intervalo en el que pueda estar comprendido el número total de palabras.
Hazlo con algún libro. O si no, imagina que lo has hecho e inventa los resultados.
19. Para hacer un sondeo electoral en un pueblo de 400 electores, aproximadamente, se va a elegir una muestra de
200 individuos. Di si te parece válido cada uno de los siguientes modos de seleccionarlos y explica por qué.
a) Se le pregunta al alcalde, que conoce a todo el pueblo, qué individuos le parecen más representativos.
b) Se eligen 200 personas al azar entre las que acuden a la verbena el día del patrón.
c) Se seleccionan al azar en la guía telefónica y se les encuesta por teléfono.
d) Se acude a las listas electorales y se seleccionan al azar 200 de ellos.
20. En una urbanización de 25 familias se ha observado la variable ―número de coches que tiene la familia‖ y se han
obtenido los siguientes datos:
0 1 2 3 1 0 1 2 3 1 0 1 1 1 4 0 1 1 1 43 2 2 1 1
a) Construye la tabla de frecuencias de la distribución.
c) Calcula la media y la desviación típica.
e) Haz el diagrama de caja.
Sol: c) x = 1,48 σ = 1,14 d) Me = 1, Q1 = 1 y Q3 = 2.
b) Haz el diagrama de barras.
d) Halla la mediana y los cuartiles.
21. El número de personas que acudieron cada día a las clases de natación de una piscina municipal fueron:
38 31 54 47 50 56 52 48 55 60 58 46 47 55 60 53 43 52 46 55
43 60 45 48 40 56 54 48 39 50 53 59 48 39 48
a) Haz una tabla de frecuencias agrupando los datos en intervalos.
b) Representa gráficamente la distribución.
Sol: c) x = 49,43
c) Halla x y σ.
σ = 7,34.
22. Un dentista observa el número de caries en cada uno de los 100 niños de un colegio y obtiene los resultados
resumidos en esta tabla:
a) Completa la tabla obteniendo x, y, z.
b) Calcula el número medio de caries.
Sol: a) y = 35 y z= 0,35 b) El número medio de caries es de 1,55.
23. El número de errores cometidos en un test por un grupo de personas viene reflejado en la siguiente tabla:
a) Halla la mediana y los cuartiles inferior y superior, y explica su significado.
b) ¿Cuál es el número medio de errores por persona?
Sol: a) Me = 2, Q1 = 1 y Q3 = 3 b) El número medio de errores por persona es ligeramente superior a 2.
24. Al preguntar a un grupo de personas cuánto tiempo dedicaron a ver televisión durante un fin de semana, se
obtuvieron estos resultados:
Dibuja el histograma correspondiente y halla la media y la desviación típica.
AYUDA: Como los intervalos no son de la misma longitud, para representar la distribución mediante un
histograma pondremos en cada barra una altura tal que el área sea proporcional a la frecuencia:
Sol: x = 2,57
σ = 1,93.
25. Estas tablas recogen la frecuencia de cada signo en las quinielas durante las 20 primeras jornadas:
a) Haz una tabla de frecuencias para el número de veces que sale el ―1‖ en cada una de las 20 jornadas:
Halla su media y su desviación típica.
b) Haz lo mismo para la ―X‖ y para el ―2‖.
c) Halla el C.V. en los tres casos y compáralos.
Sol: a) x = 7,45 σ = 1,96. b) EQUIS: x = 4,3 σ = 1,71 DOSES: x = 2,25
c) UNOS: CV = 0,2631 EQUIS: CV = 0,3977 DOSES: CV = 0,64.
σ = 1,44.
26. Cada alumno de un grupo cuenta el número de personas y el número de perros que viven en su portal. Suman sus
resultados y obtienen una muestra con la que se puede estimar el número de perros que hay en su ciudad. Por
ejemplo, supongamos que en su observación obtienen un total de 747 personas y 93 perros. Y saben que en su
ciudad viven 75 000 personas.
a) ¿Cuántos perros estiman que habrá en la ciudad?
b) ¿Cómo es de fiable esta estimación?
c) ¿Es aleatoria la muestra que han utilizado?
Sol: a) 9 337 perros, aproximadamente.
27. Para hacer un estudio sobre los hábitos ecológicos de las familias de una ciudad, se han seleccionado por sorteo las
direcciones, calle y número, que serán visitadas. Si en un portal vive más de una familia, se sorteará entre ellas la
que será seleccionada. ¿Obtendremos con este procedimiento una muestra aleatoria?
28. Se ha medido el nivel de colesterol en cuatro grupos de personas sometidas a diferentes dietas. Las medias y las
desviaciones típicas son las que figuran en esta tabla:
Las gráficas son, no respectivamente:
Asocia a cada dieta la gráfica que le corresponde.
29. Completa la tabla de esta distribución en la que sabemos que su media es 2,7.
Sol: 5.
30. Dos distribuciones estadísticas, A y B, tienen la misma desviación típica.
a) Si la media de A es mayor que la de B, ¿cuál tiene mayor coeficiente de variación?
b) Si la media de A es el doble que la de B, ¿cómo serán sus coeficientes de variación?
Sol: a) B tiene mayor coeficiente de variación. b) El coeficiente de variación de A es la mitad que el de B.
31. La validez de la información que nos proporciona una encuesta depende, en gran medida, de la cuidadosa
elaboración del cuestionario. Algunas características que deben tener las preguntas son:
— Ser cortas y con un lenguaje sencillo.
— Sus esquemas deben presentar opciones no ambiguas y equilibradas.
— Que no requieran esfuerzo de memoria.
— Que no levanten prejuicios en los encuestados.
Estudia si las siguientes preguntas son adecuadas para formar parte de una encuesta y corrige los errorres que
observes:
a) ¿Cuánto tiempo sueles estudiar cada día?
Mucho
Poco
Según el día
b) ¿Cuántas veces has ido al cine este año?
c) ¿Qué opinión tienes sobre la gestión del director?
Muy buena
Buena
Indiferente
d) ¿Pierden sus hijos el tiempo viendo la televisión?
Sí
No
e) ¿En qué grado cree usted que la instalación de la planta de reciclado afectaría al empleo y a las condiciones
de salud de nuestra ciudad?
32. En una fábrica se ha medido la longitud de 1 000 piezas de las mismas características y se han obtenido los datos
que puedes ver en esta tabla.
a) Representa el histograma correspondiente.
b) Se consideran aceptables las piezas cuya longitud
está en el intervalo [75, 86].
¿Cuál es el porcentaje de piezas defectuosas?
Sol: b) 9,25% de las piezas serán defectuosas.
33. Se ha pasado un test de 80 preguntas a 600 personas. Este es el número de respuestas correctas:
a) Comprueba que la mediana está en el intervalo [40-50). Asígnale un valor repartiendo homogéneamente
los 105 individuos que hay en el intervalo.
b) Haz lo mismo para los cuartiles.
Sol: a) Me = 43,33 b) Q1 = 26,66 Q3 = 59,41.
1.
AUTOEVALUACIÓN
En una clase de 4º ESO se ha realizado un examen final de tipo test que constaba de 30 preguntas. El número de
respuestas
15 10 30 5 25
20 25 5 25 30
30 25 10 15 20
20 10 5 15 30
a) Resume estos datos mediante una tabla de frecuencias.
b) Representa gráficamente esta distribución.
2. Hemos preguntado las edades a un grupo de 50 personas. Los resultados obtenidos se reflejan en la tabla siguiente:
EDAD
0, 5
5, 10
10, 15
15, 20
20, 25
25, 30
Nº DE PERSONAS
4
8
10
9
17
2
Halla la media y la desviación típica.
3. En la siguiente tabla hemos resumido los resultados obtenidos al lanzar un dado 120 veces:
Nº OBTENIDO
1
2
3
4
5
6
Nº DE VECES
18
30
21
25
17
9
Calcula Me, Q1, Q3 y p20.
4. a) Los tiempos que un grupo de personas han empleado en hacer un test se distribuyen entre 0 y 50 minutos.
Construye el diagrama de caja sabiendo que Q1 = 23, Me = 34 y Q3 = 39.
b) En un grupo, A, de personas, la media de edad es 16,4 años con una desviación típica de 2,1.
En otro grupo, B, la media de edad es 4,3 años, y la desviación típica, 1,8. Calcula el coeficiente de variación
en los dos casos y compara la dispersión de ambos grupos.
5. a) En un centro universitario se desea conocer el número de estudiantes que se financian sus estudios. Para ello,
el encuestador se pone en la parada del autobús de la universidad un día laborable de 11 h a 12 h y pregunta a
100 estudiantes. Reflexiona si el procedimiento de selección para obtener una muestra aleatoria es adecuado.
b) Interpreta el siguiente diagrama de caja relativo a las calificaciones obtenidas por un grupo de estudiantes:
6. En una gasolinera estudian el número de vehículos que repostan a lo largo de un día, obteniendo:
HORAS
0, 4
4, 8
8, 12
12, 16
16, 20
20, 24
Nº DE VEHÍCULOS
6
14
110
120
150
25
Calcula Me , Q3 y p80