Preuniversitario Esperanza Joven Cinemática III

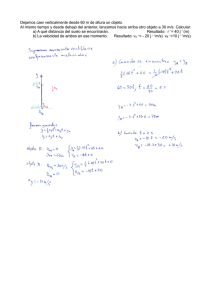
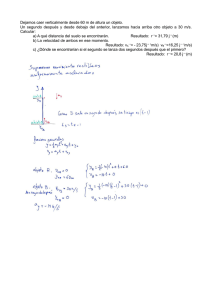
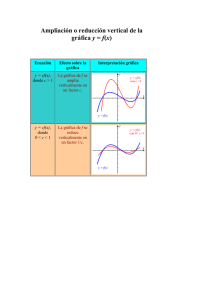
Preuniversitario Esperanza Joven
Curso Fı́sica Intensivo, Módulo Común
Guı́a 4
Cinemática III
Nombre:
Fecha:
Caı́da libre
Cualquier objeto que cae libremente experimenta una aceleración dirigida hacia abajo, independiente del
movimiento inicial del objeto. Este movimiento corresponde a un MRUA pero dirigido en la abscisa (coordenada vertical). Por lo tanto se ocuparán las mismas fórmulas para movimientos en el eje x pero esta vez
en el eje y.
Por simplicidad en los cáculos, se tomará x0 = 0 m.
1
x(t) = − · a · t2 ,
2
v(t) = −g · t,
a(t) = −g = constante.
El signo negativo aparece porque se ha tomado negativo hacia abajo.
Lanzamientos verticales
El lanzamiento vertical hacia abajo es similar a la caı́da libre (MRUA), con la diferencia que la velocidad
inicial es diferente de cero (~v0 = ~0).
El lanzamiento vertical hacia arriba, es un movimiento rectilı́neo uniformemente retardado. Si tomamos
positivo hacia arriba las ecuaciones que rigen a estos movimientos son las siguientes
1
· a · t2 ,
2
v(t) = ±v0 − g · t,
x(t) = ±v0 · t −
a(t) = −g = constante.
Recordar que por convención, si la velocidad inicial es positiva el lanzamiento es vertical hacia arriba y
viceversa, todo esto para el cálculo de desplazamiento y velocidad instatánea. En el caso que se requiera
distancia recorrida o rapidez instantánea, se debe tomar la magnitud del resultado.
Análisis del movimiento de ida y vuelta
Las expresiones que se dan a continuación nos permiten calcular el tiempo de subida y la altura máxima
alcanzada por el cuerpo
v0
,
g
v2
= 0 .
2·g
tsubida =
hmax
En las expresiones anteriores se muestra que, en estos movimientos, la masa del cuerpo es indiferente.
El tiempo de subida es proporcional a la velocidad
inicial, y la altura máxima es proporcional con la velocidad inicial al cuadrado. Notar que con un sencillo
análisis de la ecuacion de itinerario podemos llegar
fácilmente a estas expresiones.
Ejercicios
1. Un cuerpo es dejado caer libremente desde un acantilado de altura h demorando un tiempo t en tocar
el suelo. El tiempo que demora en tocar el suelo si lo dejamos caer desde un acantilado de altura 4h
es
A) t
B) 2t
C) 4t
D) 8t
E) 10t
2. En el planeta “Namek” la gravedad es la mitad que la nuesta. Si lanzamos verticalmente hacia arriba
un cuerpo a 10 m/s en la Tierra y en “Namek” a 20 m/s las alturas máximas respectivamente son
A) 5 m y 10 m
B) 10 m y 20 m
C) 5 m y 40 m
D) 40 m y 5 m
E) 40 m y 10 m
3. Una bola de billar es lanzada verticalmente hacia arriba desde la base de un edificio de 80 m de altura.
Si la velocidad inicial es 40 m/s, es correcto afirmar que transcurridos
A) 4 s regresa al lugar de lanzamiento.
B) 4 s se encuentra en la parte superior del edificio.
C) 4 s la aceleración es nula.
D) 8 s la velocidad media es 2 m/s.
E) 8 s la rapidez media es nula.
4. Al lanzar verticalmente hacia abajo una canica ésta tiene
I) velocidad incial cero.
II) aceleración constante.
III) velocidad y aceleración con igual sentido y dirección, durante su recorrido.
Es (son) verdadera(s)
A) Sólo I
B) Sólo I y II
C) Sólo I y III
D) Sólo II y III
E) I, II y III
5. Una pelota de fútbol de 7 kg se deja caer desde una altura de 80 m. ¿Cuánto tiempo tarda en llegar al
piso=
A) 2 s
B) 4 s
C) 8 s
D) 12 s
E) 16 s
6. En la Fig., el cuerpo A tiene el doble de masa que B. Si en un mismo instante soltamos A y lanzamos B
verticalmente hacia arriba con rapidez inicial v0 , de manera que en C queda en reposo por un instante,
entonces
I) ambos cuerpos experimentan la misma aceleración.
II) ambos tardan el mismo tiempo en recorrer la distancia H.
III) ambos impactan el suelo con rapidez v0 . De estas apreciaciones es(son) verdadera(s)
A) Sólo II
B) Sólo III
C) Sólo I y II
D) Sólo II y III
E) I, II y III