Energía libre de Gibbs y Helmholtz Entropía y Equilibrio Potencial
Anuncio

Clase1.doc
TERMODINÁMICA QUÍMICA I
1
Ws = (H2 - T S2) - (H1 - T S1) + T Sgen
H - TS es la energía libre de Gibbs G.
Para un cambio a T y V constante:
Es posible obtener otras formas de la Ecuación fundamental partiendo de la primera ley y de las
definiciones de entalpía y Energía libre de Helmholtz:
Para la Energía Interna:
dU = TdS – PdV , entonces U = U(S,V)
∂
∂
+
⇔
+
≥
Para la entalpía:
H = U + PV
dH = dU + PdV +VdP, entonces dH = TdS + VdP, entonces H = H(S,P)
∂
∂
]d
^d
_
h ff g
e
b a
k ii j
]d
_d
`
h ff g
e
c a
k ii j
∂
∂
∂
∂
⇔
+
∂
∂
∂
∂
+
H
+
O
S
R
W
YP
ZP
[
K II J
O
T S
N LL M
Q
S
R
W
YP
ZP
[
K II J
Q
T S
N LL M
=
U
R
X
YP
Z
KI J
T U
NL M
∂
∂
V
R
YPX
[
KI J
T V
NL M
T
R
+
son equivalentes al potencial químico.
\
\
Potencial Químico
son equivalentes al potencial químico.
7
7
δ
−
∂
∂
8@
9@
:
D BB C
A
> =
G EE F
8@
;@
<
D BB C
A
? =
G EE F
∂
∂
a T y V constantes δQ = dU, entonces:
TdS – dU ≥ 0 ó dU - TdS ≤ 0
dA ≤ 0
Entonces para un cambio espontáneo de 1 a 2 se requiere que:
A2 - A1 ≤ 0
Equivalentemente para Gibbs.
Para la Energía Libre de Helmholtz:
De la definición de la Energía libre de Gibbs:
G = H – TS, G = U + PV – TS, diferenciando se tiene:
A = U – TS
dA = dU – TdS – SdT, entonces dA = – SdT – PdV, entonces A = A(T,V)
dG = dU + PdV + VdP – TdS – SdT
∂
∂
+
∂
∂
+
∂
∂
Por otra parte, diferenciando G numéricamente, se tiene:
JAIME AGUILAR
09/09/2004
JAIME AGUILAR
l
+
s
w
v
}t {
~t
o mm n
s
x w
r pp q
u
w
v
{
}t
~t
o mm n
u
x w
r pp q
=
y
v
|
}t
om n
x y
rp q
∂
∂
z
v
}t|
~
om n
x z
rp q
Entonces: dG = VdP – SdT, y G = G(T,P)
x
v
Pero de la primera ley se tiene: dU = Q + W = TdS – PdV
09/09/2004
#
+
*
.
2
4+
5+
6
& $$ %
*
/ .
) '' (
∂
∂
,
.
2
4+
5+
6
& $$ %
,
/ .
) '' (
+
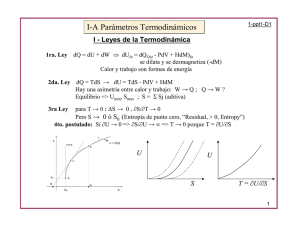
Pero de la segunda ley, dU también tiende a un mínimo en el equilibrio, entonces
Entropía y Equilibrio
De la desigualdad de Clausius:
∂
∂
0
3
4+
5
&$ %
/ 0
)' (
=
U2 - U1 = Ws + T (S2 - S1) - T Sgen
Despejando Ws
∂
∂
1
4+3
6
&$ %
/ 1
)' (
Ws = G2 - G1 + T Sgen
+
Dado que esta ecuación es suficiente para expresar el estado termodinámico de una mezcla, a ésta se
le denomina Ecuación Fundamental.
/
-
∆U = Ws + T∆S - T Sgen
+µ
dU = - PdV + δWs + TdS - T Sgen
+µ
−
U2 - U1 = - P(V2 - V1 ) + Ws + T (S2 - S1) - TSgen
Entonces:
=
∆U = -P∆V + Ws + T∆S - T Sgen
δQ(Id) = TdS y δQ(Id) = T Sgen
Por lo que dG es:
dU = - PdV + δWs + TdS - T Sgen
El calor real transferido es menor que el ideal.
El efecto de adicionar pequeñas cantidades a la mezcla será mayor para un componente que para
otros, y dado que G se relaciona con la condición de equilibrio, ésta diferencial está asociada con una
propiedad conocida como el potencial químico, µi.
!
Para un cambio a T y P constante:
+
Las dos primeras diferenciales parciales corresponden al volumen y la entropía (con signo contrario).
Las siguientes corresponden al efecto sobre la energía de Gibbs de adicionar pequeñas cantidades de
un componente manteniendo todas las demás cantidades constantes.
"
δQ(real) = δQ(Id) - δQ(no Id)
Wid = Wreal - Wno id
2
dU = - PdV + δWs + δQ
Similarmente el calor puede expresarse en dos
contribuciones:
Ws = A2 - A1 + T Sgen
Si no hay irreversibilidades, el trabajo máximo
que se puede obtener es ∆A, puede verse
como:
∂
+
∂
U - TS es la energía libre de Helmholtz A.
∂
+
∂
dU = δW + δQ
∂
+
∂
Ws = (U2 - T S2) - (U1 - T S1) + T Sgen
Planteando la primera ley de la termodinámica:
TERMODINÁMICA QUÍMICA I
∂
=
∂
Energía libre de Gibbs y Helmholtz
Se distingue entre el trabajo de flujo y otro tipo
de trabajo δWs.
Clase1.doc
+
Clase1.doc
TERMODINÁMICA QUÍMICA I
3
son equivalentes al potencial químico.
∂
⇔
∂
∂
∂
Criterios del Equilibrio:
Dado que de la segunda ley dU – TdS ≤ 0 (a volumen constante), se tiene que los cambios
espontáneos a energía interna constante son aquellos donde la entropía crece. La entropía crecerá
hasta donde pueda (máximo)
Por otro lado, los cambios espontáneos para entropía constante, son aquellos donde la energía interna
disminuye (hasta un mínimo).
09/09/2004
JAIME AGUILAR