Sesión 6 - S3 amazonaws com

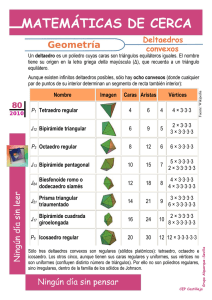
ACTIVIDADES PARA LA
SESIÓN SEXTA
AUTOR: Begoña Soler de Dios1
Máster en Profesor de Educación Secundaria Esp. Matemáticas
Universidad de Valencia
1
[email protected]
Modelización (Geometría)
Enero 2014
Sesión 6
POLIEDROS ARQUIMEDIANOS
1.
¿Qué se ve en la imagen? ¿Cuántos “trozos” negros? ¿Cuántos blancos? ¿Cuántos hay en
total, negros y blancos?
En la imagen podemos ver una pelota que geométricamente se llama
icosaedro truncado. Este poliedro se crea al truncar el icosaedro de
forma que el corte se realiza por una distancia adecuada para que por
cada cara del poliedro nos aparezca un polígono regular que tenga el
doble número de lados que el polígono de las caras del poliedro. En este
caso, al tratarse de truncar un icosaedro, las caras del poliedro de partida
tenían tres caras por lo que al truncarse tendrá seis. Es decir, como cada hexágono
corresponde a una cara del icosaedro, habrá veinte “trozos” blancos. Como los “trozos” negros
son el resultado del corte del truncamiento, al truncarse por cada vértice habrá doce “trozos”
negros. Es decir, en total habrá 32 “trozos” o caras.
2.
Un modelo más sencillo: ¿Con qué poliedro puede relacionarse? ¿Qué se mantiene y
cambia en la transformación? ¿Cómo podemos determinar C, V, A… de este sólido a partir
del cubo?
Esta figura es un cubo truncado y se obtiene al truncar, del mismo modo
que en el apartado anterior, un cubo cortando sus vértices. Como en el
cubo concurren tres caras en cada vértice, el resultado del corte será un
triángulo.
Tras la transformación se mantienen las caras del poliedro inicial pero con diferente número
de lados, concretamente el doble y además aparecen ocho caras más que provienen de los
vértices truncados. También sigue manteniéndose el orden de los vértices del poliedro, tres
(dos polígonos que provienen de caras y un polígono que proviene del truncamiento del
vértice).
Para determinar C, V y A nos basamos en que se forma a partir del truncamiento del cubo. El
número de caras del cubo es seis, al hacerse los cortes en cada uno de los vértices
Universidad de Valencia
2
Modelización (Geometría)
Enero 2014
obtendremos ocho caras más adicionales ya que el cubo tiene ocho vértices, es decir, nuestra
figura tendrá seis caras que serán octógonos y ocho caras que serán triángulos (6+8=14). El
número de aristas también lo podemos calcular a partir del cubo, habrá 36, las que provienen
de los vértices del cubo más las que provienen de las caras originales. Es decir, habrá tres
aristas nuevas creadas por cada truncamiento de un vértice del cubo, por lo que se añaden
3*8=24 aristas a las 12 iniciales del cubo. Finalmente también podemos calcular el número de
vértices teniendo en cuenta que al truncarse un vértice surgen tres vértices nuevos por lo que
8*3=24 vértices.
3. Sigamos de manera sistemática: ¿Qué tienen en común los poliedros de la figura?
Estos poliedros tienen en común que se han obtenido a partir de sólidos platónicos
truncándolos como se explica en el ejercicio uno. Es decir, el corte se realiza por una distancia
adecuada para que por cada cara del poliedro nos aparezca un polígono regular que tenga el
doble número de lados que el polígono de las caras del poliedro de partida.
Los poliedros que aparecen en las figuras son el tetraedro truncado, el octaedro truncado, el
dodecaedro truncado y el icosaedro truncado, que se obtienen cortando los vértices (tal y
como se ha explicado anteriormente) del tetraedro, octaedro, dodecaedro e icosaedro
respectivamente.
3
Universidad de Valencia
Modelización (Geometría)
4.
Enero 2014
¿Hay otros poliedros con caras regulares? ¿Hay otras posibilidades para cortar los
vértices de los poliedros regulares de manera que por cada cara se siga obteniendo un
polígono regular? ¿Qué nuevos poliedros encontramos? ¿Con qué poliedros regulares se
relacionan? ¿Qué características numéricas tienen? ¿Qué otras propiedades tienen? En la
última figura se muestran dos poliedros regulares y el cuboctaedro. ¿Qué explicaciones das
al nombre que tiene? ¿Cómo nombras los sólidos de la última figura?
Además de los sólidos platónicos y de los cinco truncados que hemos visto anteriormente,
existen más poliedros con las caras regulares: cuboctaedro, icosidodecaedro pequeño
rombicuboctaedro, gran rombicuboctaedro, pequeño icosidodecaedro, gran icosidodecaedro,
cubo chato y dodecaedro chato. Sus características numéricas, propiedades y sus relaciones
con otros poliedros aparecen en un documento anterior llamado “Poliedros Arquimedianos”
(preg. 5 y 6 del pdf allí).
En la figura inferior aparecen un dodecaedro, un icosaedro y un icosidodecaedro. El nombre
icosidodecaedro es debido a que este sólido es la intersección del icosaedro y el dodecaedro.
4
Universidad de Valencia
Modelización (Geometría)
Enero 2014
TRUNCAMIENTO, SECCIONES Y SIMETRÍAS DE LOS POLIEDROS
REGULARES
7.
¿Qué forma tiene la sección del cubo perpendicular al eje que pasa por vértices opuestos
y equidista de ellos? Puedes dar diferentes tipos de respuesta más o menos visuales. Por
ejemplo, para responder te puedes basar en las figuras siguientes. Responde también a esta
actividad de otras maneras.
Situándonos en una de las esquinas del cubo y cortamos esa esquina con un ángulo apropiado
de modo que la sección producida será un triángulo equilátero. Si seguimos moviéndonos
mediante planos paralelos al corte primero realizado, evidentemente, aparecerán triángulos
mayores hasta que se llegue a los vértices, ese será el triángulo equilátero mayor. En el caso de
seguir haciendo cortes las secciones se convertirán en hexágonos irregulares, llegando un
momento en el que el hexágono será regular y nuevamente volverán a ser irregulares hasta
que se llegue a los vértices del cubo, de donde aparece nuevamente el triángulo equilátero de
partida.
8.
Planos de simetría (PS) y ejes de rotación (ER) de los poliedros regulares. Determinas los
PS y ER de cada uno de los poliedros regulares. Razonar la forma que tienen, cuántos hay de
cada tipo y las relaciones que hay entre ellos (los planos de simetría y los ejes de rotación).
Indicar también la forma de otras secciones que dividen al poliedro regular en dos partes
iguales pero que no son planos de simetría.
-Planos de simetría:
CUBO:
1. Hay planos paralelos a pares de caras opuestas. 3
5
Universidad de Valencia
Modelización (Geometría)
Enero 2014
2. Hay planos que pasan por pares de aristas opuestas. 6
OCTAEDRO:
1. Planos perpendiculares al segmento que une pares de vértices opuestos. 3
2. Planos de simetría que pasan por puntos medios de pares de aristas opuestas. 6
TETRAEDRO:
1. Contienen una de sus aristas y pasa por el punto medio de otra. 6
OCTAEDRO e ICOSAEDRO:
1. Pasan por un par de aristas opuestas y cortan por el punto medio a otro par de
aristas opuestas. 15
Tres de estos planos de simetría son perpendiculares dos a dos, como ocurre en el modelo de
las simetrías del cubo y del octaedro.
-Ejes de rotación:
CUBO y OCTAEDRO:
Como las caras del cubo se corresponden con los vértices del octaedro, cabe pensar que los
ejes se corresponden.
1. El octaedro tiene 3 ejes de rotación de orden 4, uno por cada par de vértices
opuestos. Cada uno es perpendicular a un plano de simetría del octaedro. En el
caso del cubo pasa por los centros de caras opuestas.
2. Pasan por vértices opuestos del cubo. Hay 4 de este tipo y son de orden 3. En el
caso del octaedro pasará por los centros de sus caras. Estos ejes no son
perpendiculares a ningún plano de simetría. Y sus cuatro posibles secciones serán
hexagolanes regulares.
3. Pasan por puntos medios de aristas opuestas. Hay seis y son de orden dos. Cada
uno de ellos será perpendicular a un plano de simetría, que en el cubo pasa por
pares de aristas opuestas, y en el octaedro por puntos medios de pares de aristas
opuestas.
DODECAEDRO e ICOSAEDRO:
1. 6 ejes de rotación de orden 5: Pasan por los centros de las caras del dodecaedro o
por los vértices opuestos del icosaedro. El plano perpendicular de cada uno de
ellos los corta en una sección de decágono regular.
2. 10 ejes de rotación de orden 3: Pasan por los centros de las caras del icosaedro y
por vértices opuestos del dodecaedro. El plano perpendicular a cada uno de ellos
corta al dodecaedro en hexágonos regulares y al icosaedro en un dodecágono no
regular.
Universidad de Valencia
6
Modelización (Geometría)
Enero 2014
3. 15 ejes de rotación de orden 2: Pasan por puntos medios de aristas opuestas y son
perpendiculares a planos de simetría del poliedro.
Los 4 ejes de rotación de orden 3 del cubo y octaedro están dispuestos exactamente de la
misma manera que 4 ejes de rotación de orden 3 del dodecaedro e icosaedro.
Los tres ejes de rotación de orden 4 del cubo y del octaedro están dispuestos exactamente de
la misma manera que 3 ejes de rotación de orden 2 del dodecaedro e icosaedro.
TETRAEDRO:
1. 3 de orden 2: Pasan por puntos medios de aristas.
2. 4 de orden 3: Pasan por un vértice del tetraedro y el centro de la cara opuesta.
Siete de estos ejes se cortan exactamente de la misma manera que siete del cubo.
RELACIÓN ENTRE EJES Y PLANOS DE SIMETRÍA:
En las rectas donde se cortan planos de simetría hay ejes de rotación que tienen un orden que
coincide con el número de planos que se cortan en esa recta.
REFERENCIAS:
Guillén G, Poliedros, Ed. Síntesis
7
Universidad de Valencia