EL BARICENTRO Y LAS MEDIANAS DE UN TRIÁNGULO. UNA

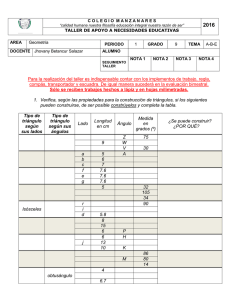
EL BARICENTRO Y LAS MEDIANAS DE UN TRIÁNGULO.
UNA EXPERIENCIA EN EL AULA
Ana Inés Battaglino – Mónica Figueroa
[email protected] – [email protected]
Estudiantes del IPA y docentes de los liceos 55 y 41, Uruguay.
Modalidad: CB- Comunicación Breve.
Nivel educativo: Nivel medio.
Palabras clave: Centro de gravedad .Medianas de triángulo.
Resumen
Uno de los principales desafíos de nuestras prácticas educativas es acompañar los
cambios que conlleva la sociedad. Estamos viviendo una sociedad de la información
donde las propuestas deben ser dinámicas, atractivas visualmente, contextualizadas y
que satisfagan las necesidades de los estudiantes. El cambio social ha permitido el
acceso a distintas herramientas tecnológicas (XO en Uruguay) por lo que se tiene que
repensar el uso de las mismas en el aula en forma eficaz. Saber aprender es una
necesidad formativa básica generada fundamentalmente por las implicaciones sociales
de las revoluciones tecnológicas.
En éste marco planteamos actividades de aula para trabajar conceptos geométricos
únicamente con el uso de la computadora. Entendemos que entre otras cosas, permitirá
a los estudiantes que tienen dificultades con los instrumentos de geometría, un mejor
desempeño y análisis propiciando mejores logros.
Las actividades se centrarán en construcciones de medianas en triángulos, observando
algunas propiedades interesantes de las mismas y su relación con el baricentro.
Desarrollo del Trabajo
En la valoración de J.Pozo la educación tiene que estar dirigida a ayudar a los
estudiantes a aprender a aprender. Promoviendo la capacidad de que éstos gestionen sus
propios aprendizajes y desarrollen un pensamiento crítico que les permita seguir
aprendiendo a lo largo de toda la vida.
Saber aprender es un factor de progreso personal y social y no cabe duda de que en la
sociedad actual, caracterizada por una nueva forma de relacionarse e interactuar con el
conocimiento,
ha
pasado
a
ser
una
necesidad
formativa
básica
generada
fundamentalmente por las implicaciones sociales de las revoluciones tecnológicas.
En el marco del Plan Ceibal de educación secundaria del ciclo básico en el cual cada
estudiante tiene acceso al software Geogebra desde su propia XO, pretendemos
incentivar, estimular y trabajar estrategias de aprendizaje utilizando esta herramienta. Es
fortaleciendo el uso de las TICs en el aula y adecuando la currícula a la actualidad que
creemos se propiciarán mejores logros en el aprendizaje.
GeoGebra Uruguay 2012
ISSN 2301-0185
223
El desafío del docente, en este nuevo escenario educativo, es incentivar a los educandos
a descubrir, conjeturar, visualizar, realizar hipótesis y potenciar sus fortalezas y en
consecuencia lograr una mayor autonomía. El docente es el responsable de utilizar la
herramienta en función de los contenidos curriculares en forma apropiada.
Pensamos que los aprendizajes logrados utilizando las TICs permiten que los
estudiantes perciban la importancia de la matemática y su vínculo con otras áreas del
conocimiento.
"Una actividad es más educativa en la medida en que permite al alumno desempeñar un
papel activo más que pasivo en situaciones de aprendizaje" (Raths)
Luego de la exploración de los alumnos con el programa Geogebra y actividades áulicas
respecto a la geometría del triángulo se abordarán las actividades que proponemos sobre
las medianas de un triángulo y algunas de sus propiedades.
El presente trabajo describe una experiencia enfocada principalmente a alumnos de
segundo año del Ciclo Básico.
Objetivos generales:
Que el alumno explorando, jugando, razonando, describiendo, explicando y
relacionando se involucre en un proceso integral obteniendo así aprendizajes
caracterizados por significados.
Objetivos específicos:
Trabajar con triángulos y la construcción de sus medianas así como también deducir y
verificar algunas de sus propiedades.
Desarrollo:
Se plantearán actividades
Ö
Trazado del baricentro. Trazado de dos medianas y deducir la Propiedad de
concurrencia de las tres medianas.
Ö Baricentro.
Ö Cálculo de las áreas de los triángulos que quedan determinados por las medianas.
Ö Triángulos rectángulos y sus medianas.
Se realizarán puestas en común y registro de las propiedades observadas.
GeoGebra Uruguay 2012
ISSN 2301-0185
224
Conclusión:
Primeramente observemos que el uso del programa Geogebra no se limita a la instancia
de clase sino que promueve una búsqueda continua que posibilita al desarrollo del
pensamiento crítico en los estudiantes.
Por otro lado consideramos que el verdadero desafío de los docentes en la actualidad, y la clave
del éxito estará en la capacidad de crear, adaptar, presentar y compartir actividades didácticas
innovadoras, mediadas por tecnología, donde ésta enriquece la práctica, genera interacción,
facilita la adopción, flexibiliza los diferentes ritmos de aprendizaje y promueve genuinos
procesos cognitivos inspiradores que enriquecen el currículo.
GeoGebra Uruguay 2012
ISSN 2301-0185
225
Referencias bibliográficas para las actividades a desarrollar
Coexeter, H.S.M.y Greitzer S.L. (1994). Retorno a la Geometría. Capítulo 1 Puntos y
líneas relacionados con el triángulo. Madrid. Ed.Euler.Col. La tortuga de Aquiles, 1.
Coexeter, H.S.M. (1971). Fundamentos de Geometría. Capítulo 1 Triángulos. MejicoBuenos Aires. Agencia para el desarrollo internacional.(A.I.D.)
Cursos en el marco del Plan Ceibal. Nuevos escenarios educativos con dotación
1:1...construyendo el conocimiento desde la práctica. Qualitas. Microsoft.
Cursos en el marco del Plan Ceibal. Herramientas sociales y Aplicaciones web 2.0 para
el Desarrollo y diseño de Nuevos espacios Aúlicos. Qualitas. Microsoft.
Zambra M. Rodríguez M y Belcredi L (1999) Geometría. Un curso de geometría
métrica para el segundo ciclo. Uruguay.Ediciones de la Plaza.
Anexo:
Planificación de la Clase:
GeoGebra Uruguay 2012
ISSN 2301-0185
226
Grupo: 2º año Ciclo Básico
Tema: Geometría del Triángulo. Medianas. Baricentro. Propiedades.
Tiempo: 2 hora clase (45´cada una)
Conocimientos previos:
•
Triángulos. Áreas y clasificación.
•
Mediatriz.
•
Ortocentro y circunferencia circunscripta.
•
Manejo del Software Geogebra.
Objetivos: Que el alumno explorando, jugando, razonando, describiendo, explicando y
relacionando se involucre en un proceso integral obteniendo así aprendizajes
caracterizados por significados.
Objetivos específicos:
Trabajar con triángulos y la construcción de sus medianas así como también deducir y
verificar algunas de sus propiedades.
Desarrollo:
Se plantearán tres actividades. En la primera se trabaja revisión de clasificación de
triángulos y construcción del baricentro.
La segunda actividad refiere a áreas de los triángulos que quedan determinados por las
medianas. Verificando que los seis triángulos son de igual área.
Luego, a partir de un triángulo rectángulo, se observará una propiedad interesante. En
todo triángulo rectángulo el ortocentro es el punto medio de la hipotenusa y por lo tanto
la mediana correspondiente a la hipotenusa, coincide con el radio.
Se dará a los estudiantes una actividad por vez.
Ö Actividad Previa:
Se realizará una actividad para agrupar a los estudiantes en equipos,
integrándolos en forma arbitraria.
Se trabajará revisando clasificación de triángulos, perímetro de un triángulo,
mediatriz, etc.
GeoGebra Uruguay 2012
ISSN 2301-0185
227
La idea es que los estudiantes además de trabajar los contenidos matemáticos
mencionados, no siempre trabajen con los mismos compañeros y se propicie la
integración en el grupo.
Para formar los grupos. Se dará una carta a cada uno de los estudiantes y se les
pedirá que “encuentren” y formen su equipo de manera que las cartas que tengan
se relacionen entre sí.
Se apuntará a formar grupos de tres estudiantes.
Los estudiantes deben buscar al resto de los integrantes de cada equipo de modo
que las tarjetas se relacionen entre sí, siempre teniendo en cuenta los conceptos
que se quieren revisar.
Para facilitar la actividad y lograr un clima adecuado de trabajo, se propone que
cada equipo esté formado por cartas de distinto color.
Se repartirá una carta por estudiante y se pedirá que quienes tienen cartas de
color naranja se paren a buscar a otros compañeros que tengan cartas de color
verde y cuyas cartas se relacionen.
Luego se hará lo mismo con quienes tienen cartas de color rojo.
Ö Algunas cartas (a modo de ejemplo)
Grupo 1
Triángulo
rectángulo.
Un triángulo con un
ángulo recto.
Grupo 2
Triángulo
isósceles.
GeoGebra Uruguay 2012
Un triángulo con
dos lados iguales.
ISSN 2301-0185
228
Grupo 3
Grupo 3
Un triángulo con
tres lados iguales.
Triángulo
equilátero.
Grupo 4
Los lados del
triángulo miden
a=3cm, b=6cm y
c=4,5cm
Triángulo
escaleno.
GeoGebra Uruguay 2012
ISSN 2301-0185
229
El perímetro del
Grupo ABC
5
triángulo
es
13,5 cm.
Grupo 5
Es una recta
perpendicular al
segmento por su
punto medio.
Mediatriz de un
segmento.
Todo punto P
perteneciente a la recta
equidista de los extremos
del segmento
considerado.
Luego de que cada grupo quedó conformado cada uno leerá su tarjeta con el fin
de chequear que lo hayan hecho en forma correcta. La idea de esta puesta en
común es detectar las posibles dificultades que hayan surgido y poder analizarlas
y ayudar a los estudiantes a superarlas. Además permitirá que toda la clase
verifique o refute lo realizado por cada equipo y se realicen, si es necesario, las
correcciones que correspondan.
Actividad- Baricentro y medianas:
Trabaja en forma ordenada siguiendo cada paso:
Ö Construye un triángulo ABC.
Ö Encuentra el punto medio del lado AB, denomínalo N.
GeoGebra Uruguay 2012
ISSN 2301-0185
230
Ö
Ö
Ö
Ö
Ö
Encuentra el punto medio del lado BC; denomínalo M. Utilizando la mediatriz
de cada segmento.
Oculta las mediatrices.
Une los puntos CN y AM.
Observa: Los segmentos que unen los puntos medios de un lado de un triángulo
con el vértice opuesto se llaman MEDIANAS.
Llama G a la intersección de las medianas obtenidas.
Traza la tercer mediana y verifica si el punto G pertenece a ella.
Observa: El punto G se llama BARICENTRO del triángulo.
¿Qué sucede si cambias de triángulo?
Arrastra uno de los puntos y responde Verdadero o Falso:
a-Las tres medianas de un triángulo concurren en el punto G sólo en el primer
triángulo.
b-Las tres medianas de un triángulo concurren en el punto G para todo triángulo
que obtuviste.
c-Las medianas miden lo mismo para todo triángulo.
d- La distancia GM es la tercera parte de la distancia GA.
Para trabajar con tus compañer@s:
Puesta en Común:
Se apuntará a la observación de la construcción de las medianas, del baricentro de un
triángulo y a la siguiente Propiedad:
Las medianas de un triángulo se dividen una a otra en razón de 2, 1.
Actividad – Áreas:
Ö Calcula el área de los seis triángulos que se determinan con las medianas del
triángulo ABC. ¿Qué concluyes?
GeoGebra Uruguay 2012
ISSN 2301-0185
231
Verificaremos si tu conclusión es correcta:
Ö Traza y mide las alturas desde el vértice G de los triángulos BEG y ECG.
En esos triángulos las alturas y las bases son___________. Por lo tanto las áreas
halladas son iguales.
Ö ¿Existen otros pares de triángulos de igual área entre si? ¿Cuáles?
Puesta en Común:
Se apuntará a la conclusión de la siguiente propiedad:
Las medianas de un triángulo lo dividen en seis triángulos de igual área.
La idea en esta actividad es que los estudiantes vean con facilidad la igualdad de
las áreas de los triángulos EBG y CEG por tener iguales la base y la altura.
Luego, se intentará que apliquen la propiedad anterior en donde se podrá
concluir que el área del triángulo GAB es igual al doble del área del triángulo
GBE.
Actividad – Triángulo Rectángulo:
Dado un triángulo ABC, rectángulo en A.
Ö Construye el ortocentro.
GeoGebra Uruguay 2012
ISSN 2301-0185
232
Ö Construye la mediana correspondiente al lado BC, ¿Qué conclusiones puedes
sacar?
Ö Observa si ocurre lo mismo cambiando C, manteniendo el triángulo rectángulo
en A.
Puesta en común:
Se pretende llegar a la conclusión de que la mediana AO es el radio de la
circunferencia circunscrita al triángulo ABC.
GeoGebra Uruguay 2012
ISSN 2301-0185
233