Problemos resueltos - Raquel Serrano Lledó

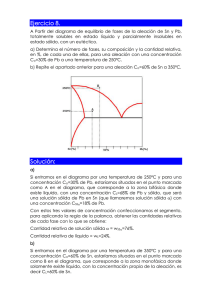
Problemas de diagramas de equilibrio
PROBLEMA 1
Los puntos de fusión del bismuto y antimonio son 271 ºC y 632,2 ºC respectivamente. Una aleación con un 50% de SB comienza a solidificar a 520 ºC formándose cristales
con un contenido en Sb de un 90%. Cuando la composición de la aleación es del 20% de
Sb la solidificación se inicia a 400 ºC separándose cristales con un 75% de Sb. Se pide:
a) Dibujar a escala el diagrama de equilibrio de este sistema, indicando sobre el los
nombres de todos los puntos, lineas y zonas.
b) Dada una aleación compuesta de un 40% de Sb indicar: la temperatura inicial de
solidificación, temperatura final de solidificación, composición química y las
cantidades relativas de las fases presentes a 426,6 ºC y dibujar la curva de
enfriamiento.
a) Diagrama de equilibrio
Diagrama Bi-Sb
700
L
600
L liquidus
500
b) Temperatura inicial de solidificación
L+α
400
L solidus
300
(ver diagrama)
T1 = 490 ºC
Temperatura final de solidificación
(ver diagrama)
200
α
100
0
T2 = 290 ºC
0
10 20 30 40 50 60 70 80 90 100
Bi
Composición química y cantidades relativas de las fases presentes a 400 ºC
A 400 ºC existen dos fases en equilibrio: líquido de composición 20 % en Sb y la solución
sólida α de composición 75 % en Sb. Las cantidades relativas de cada fase serán:
A 400 ºC
L de 20 % Sb - 80 % Bi
y
α de 75 % Sb - 25 % Bi
%α
=
40 − 20
⋅100 = 36.4 %
75 − 20
Luego % L = 63.6 %
Es decir, que a 400 ºC un 63.6% en peso es líquido de composición química 20 % Sb y un
1
Problemas de diagramas de equilibrio
36.4%corresponde a la fase α de composición química 75 % Sb.
Idéntico resultado se obtiene haciendo el balance de masas para la fase α
40 − 20
%α =
⋅ 100 = 36.4 %
Luego % L = 63.6 %
75 − 20
Curvas de enfriamiento
Curva enfriamiento 40 % Sb
1000
Temperatura
800
600
490ºC
400
290ºC
200
0
Tiempo
PROBLEMA 2
El bismuto y el cadmio se supone que son totalmente solubles en estado liquido y
totalmente insolubles en el estado sólido, formando un eutéctico a 143,3 ºC con un
contenido en Cd de un 40% . Se pide
a) Dibujar a escala el diagrama de equilibrio de este sistema, indicando sobre él los
nombres de todos los puntos, líneas y zonas.
b) Dada una aleación compuesta de un 70% de Cd, indicar: la temperatura inicial de
solidificación, temperatura final de solidificación, composición química y las cantidades
relativas de las fases presentes a una temperatura 40 ºC por debajo de la temperatura
inicial de solidificación y dibujar la curva de enfriamiento.
DATOS:
2
Punto de fusión Bi = 271 ºC
Punto de fusión Cd = 321 ºC
Problemas de diagramas de equilibrio
a) Diagrama de equilibrio
Diagrama Bi-Cd
400
L
350
L liquidus
300
b.1) Temperatura inicial de solidificación
L liquidus
250
(ver diagrama)
200
T1 = 230 ºC
Bi + L
150
(ver diagrama)
Cd + L
L solidus
100
b.2) Temperatura final de solidificación
punto
eutéctico
Bi +Cd
50
0
T2 = 143.3 ºC
0
10 20 30 40 50 60 70 80 90 100
Bi
Cd
b.3) Composición química y cantidades relativas de las fases presentes a una temperatura
30ºC por debajo de la temperatura inicial de solidificación
A 200 ºC hay dos fases en equilibrio:
Porcentaje de cada fase:
%L =
L (60 % Cd) + Cd
100 − 70
⋅ 100 = 75 %
100 − 60
Luego % Cd es 25 %
b.4) Curvas de enfriamiento
Curva enfriamiento 70 % Cd
600
Temperatura
500
L
400
300
200
270ºC
L + Cd
143.3º
L + Cd + Bi
100
Cd + Bi
0
Tiem po
3
Problemas de diagramas de equilibrio
PROBLEMA 3
Los puntos de fusión del plomo y del estaño son 326,6 ºC y 232,2 ºC respectivamente. Cuando la aleación contiene un 60% de Sn forma un eutéctico que solidifica a
182,2 ºC. La solubilidad máxima en estado sólido, a esta temperatura del Sn en el Pb es
del 19% y del Pb en el Sn del 2.5%. Suponiendo que la solubilidad mutua a la
temperatura ambiente es despreciable. Se pide:
a) Dibujar el diagrama.
b) Composición química y cantidades relativas de las fases presentes de una aleación del
40 % de Sn a 200 y 182 ºC.
c) Dibujar la curva de enfriamiento de esta aleación.
d) Representar la microestructura de dicha aleación, a temperatura ambiente, con
indicación de las fases y constituyentes estructurales.
e) ¿Podría esa misma aleación presentar microsegregación (coring)?
a) Diagrama de equilibrio
Diagrama Pb - Sn
350
L
Temperatura
300
250
L+α
200
L+β
α
150
β
α+β
100
50
0
0
Pb
10 20 30 40 50 60 70 80 90 100
Porcentaje en peso de Sn
Sn
b) Composición química y cantidades relativas de las fases presentes de una aleación del
4
Problemas de diagramas de equilibrio
40 % de Sn a 200 y 182 ºC.
A 200 ºC : L (53 % Sn) + α (17 % Sn)
%α
=
53 − 40
⋅ 100 = 36.11 %
53 − 17
Luego % L = 63.89 %
A 182 ºC : α (19 % Sn) + β (97.5 % Sn)
%α
=
97.5 − 40
⋅ 100 = 73.25 %
97.5 − 19
Luego % β = 26.75 %
c) Curva de enfriamiento
curva enfriamiento 40 % Sn
Temperatura
400
350
L
300
250
230º
200
182.2ºC
150
L+ α
L + α+ β
α+β
100
Tiempo
d ) Representar la microestructura de dicha aleación, a temperatura ambiente, con
indicación de las fases y constituyentes estructurales.
A 25 ºC existen en equilibrio dos fases: solución sólida α ( 0% Sn, es decir 100% Pb) y
solución sólida β ( 100 % Sn) supuesta la solubilidad mutua despreciable, porcentaje de cada
fase:
5
Problemas de diagramas de equilibrio
%α
=
100 − 40
⋅ 100 = 60 %
100 − 0
Luego % β es del 40 %
Como constituyentes existirán a temperatura ambiente: constituyente eutéctico y α, en
proporciones:
40 − 0
% eutéctico =
⋅ 100 = 66.67 %
60 − 0
Luego % α libre 33.33%
Granos blancos: granos de sol. sol. α
Matriz continua sombreada: Eutéctico [α + β]
¿Podría esa misma aleación presentar microsegregación (coring)?
Si podría presentar microsegregación. Obsérvese que una aleación de composición entre 0 y 19
% Sn (o entre el 97.5 y 100 % Sn) solidifica en un rango de temperaturas, por ejemplo la
solidificación de una aleación del 10 % Sn comienza a los 300 º C y termina a los 250 ºC, la
fase sólida α formada a 300 º C tiene una composición del 3% en Sn mientras que a 250 ºC
todo el sólido α formado tendrá una composición del 10 % Sn, Esto significa que el sólido
formado a 300 º C debe cambiar su composición, aumentando el porcentaje de soluto que debe
difundirse desde el líquido hacia el interior del grano formado homogeneizando la composición
a cada temperatura. Cuando la velocidad de enfriamiento no permite que se eliminen los
gradientes de concentración la estructura granular formada estará fuertemente segregada ,
denominándose microsegregación o “coring”. Este fenómeno puede ocurrir en el proceso de
solidificación de cualquier aleación que lo haga en un margen de temperaturas.
6
Problemas de diagramas de equilibrio
PROBLEMA 4
Usando los datos del problema anterior calcular la densidad de una soldadura que
contiene un 60 % Pb y 40 % Sn, que ha sido equilibrada a 25 ºC. Las densidades de la fase
α y β son respectivamente 11,3 mgr/mm3 y 7,3 mgr/mm3.
De la solución del apartado d) del problema anterior, sabemos que a 25 ºC existen en equilibrio
dos fases: solución sólida α y solución sólida β y que el porcentaje en peso de cada fase es:
% α = 60 % y % β = 40 %.
Tomando como base 100 mgr de mezcla tendremos:
100 mgr soldadura = 60 mgr de fase α + 40 mgr de fase β
Los volúmenes ocupados por cada fase serán:
α→
60 mgr
= 5.31 mm3
3
11.3 mgr / mm
β→
40 mgr
= 5.48 mm3
3
7.3 mgr / mm
El volumen total ocupado por los 100 mgr de soldadura será: 5.31 mm3+ 5.48 mm3 = 10.79 mm3
con lo que la densidad será:
d=
100 mgr
= 9.27 mgr / mm3
3
10.79 mm
Idéntico resultado se obtiene aplicando la regla de las mezclas sobre las fracciones
volumétricas, es decir:
d = fα · dα + fβ · dβ
donde d es la densidad de la mezcla, dα y dβ son las densidades de las fases α y β
respectivamente y fα y fβ son las fracciones volumétricas de las fases α y β respectivamente.
En efecto, de lo anterior calculado se deduce que las fracciones de volumen son:
fα =
5.31
= 0.492
10.79
fβ =
5.48
= 0.508
10.79
7
Problemas de diagramas de equilibrio
De donde:
d = fα ⋅ dα + f β ⋅ d β = 0.492 ⋅11.3 mgr / mm 3 + 0.508 ⋅ 7.3 mgr / mm 3 = 9.268 mgr / mm 3
PROBLEMA 5.
Del sistema Pt-Ag, se sabe que el platino, de punto de fusión 1750 ºC, disuelve a la
temperatura de 1180 ºC el 15 % de Ag formando una solución sólida α. A esta
temperatura (1180 ºC) tiene lugar una reacción peritéctica entre α y el líquido de
composición 70 % Ag, formándose una solución sólida β que contiene un 55 % Ag. A 800 º
C la solubilidad de Ag en Pt es del 10 % y la del Pt en Ag del 40 %. Se pide:
a) Dibujar el diagrama de equilibrio suponiendo rectas todas las líneas e indicar las fases
presentes en cada región.
b) Curvas de enfriamiento de las aleaciones del 12, 45, 55 y 70 % de B.
c) Para una aleación de un 30% de B y a la temperatura de 500 ºC, calcular la cantidad y
composición de cada una de las fases presentes.
a) Diagrama de equilibrio.
d) Curvas de enfriamiento de las aleaciones del 12, 45, 55 y 70 % de B.
2000
diagrama Pt-Ag
L
Temperatura
1500
α+L
β+ L
1180 ºC
α
1000
β
α+β
500
0
0
Pt
8
10
20
30
40
50
60
70
80
90
100
Ag
Problemas de diagramas de equilibrio
2000
Temperatura
12 % Ag
45 %
65 %
70 %
1500
1180 ºC
1000
500
Tiempo
d) Para una aleación de un 30% de B y a la temperatura de 500 ºC, calcular la cantidad y
composición de cada una de las fases presentes.
A 500 ºC coexisten en equilibrio la fase α de composición 5 % de Ag y la fase β de
composición 65 % Ag. Porcentaje en peso de cada fase:
65 − 30
%α =
⋅100 = 58.3%
% β = 41.7%
65 − 5
PROBLEMA 6
Con el diagrama de equilibrio Au - Bi de la figura se pide determinar:
a) Fases presentes en las diversas regiones. Reacciones invariantes que se verifican.
b) Fórmula del compuesto intermetálico sabiendo que contiene 65,4 % de Au.
c) Indicar si existen soluciones sólidas extremas o intermedias.
d) Análisis de fases en el enfriamiento lento de una aleación del 40 % Au desde 500 ºC
hasta temperatura ambiente. Microconstituyentes a temperatura ambiente.
e) Curva de enfriamiento de las aleaciones del 40 y 65,4 % de Au.
DATOS:
PAu = 196,96 gr/mol
PBi = 208,98 gr/mol
9
Problemas de diagramas de equilibrio
1200
L
1000
800
L+Au
600
400
371 ºC
L+Bi
L+C
241 ºC
C+Au
200
Bi+C
0
Bi0
20diagrama
30 40 Bi-Au
50 60
10
70
80
90 Au
100
a) Reacciones isotérmicas
Peritéctica:
371º C
L(32% Au ) + Au ⎯⎯ ⎯
⎯→ C (65.4% Au )
Eutéctica:
341º C
L(12.5% Au ) ⎯⎯ ⎯
⎯→ Bi + C (65.4% Au )
b) Fórmula del compuesto
% en peso de Au = 65,4
La fórmula será de la forma: Aux Biy,
% en peso de Bi = 34,6
x
representa la relación entre el número de átomos o de
y
moles de Au y Bi, luego:
masa de Au =
x PAu
65.4
=
100 x PAu + y PBi
65.4 x PAu
=
34.6 y PBi
masa de Bi =
⇒
34.6
y PBi
=
100 x PAu + y PBi
x 65.4 ⋅ 208.98
=2
=
y 34.6 ⋅196.96
Por tanto, los valores de x e y son: x = 2 y = 1. La fórmula del compuesto es: Au2 Bi
10
Problemas de diagramas de equilibrio
c) Indicar si existen soluciones sólidas extremas o intermedias
Puede comprobarse que el Au y el Bi no son solubles en estado sólido, por lo que no existe
formación alguna de soluciones sólidas, ni extremas ni intermedias. Solo a la composición fija
de 65,4 Au - 34,6 Bi tiene lugar la formación del compuesto Au2 Bi, que es una fase intermedia
que bien podría ser una solución sólida intersticial, o aún más probable una fase de Laves.
d) Análisis de fases en el enfriamiento lento de una aleación del 40 % Au desde 500 ºC
hasta temperatura ambiente.
− a 500ºC, fases: L(40% Au)
− entre 450 ºC y 371 ºC las fases en equilibrio son Au y Líquido cuya composición varía
desde el 40 % hasta el 32 % de Au.
− A 371 ºC tiene lugar una reacción peritéctica tras la cual las fases en equilibrio son:
L(32%Au) + C(65.4 %Au)
65.4 − 40
%L =
⋅100 = 76%
65.4 − 32
% C= 24 %
− Entre 371 ºC y 241 ºC existen en equilibrio del compuesto C(65.4 % Au) y líquido cuya
composición va variando entre 32 y 12.5 % Au.
− A 241 ºC tiene lugar una reacción eutéctica tras la cual las fases en equilibrio son: Bi y C
65.4 − 40
% Bi =
⋅100 = 38.8%
65.4 − 0
% C = 61.2 %
− A temperatura ambiente existe un 38.8% de Bi y un 61.2 % de Au2Bi de composición 65.4
% Au.
Microconstituyentes a temperatura ambiente.
A 241 ºC el líquido de composición 12,5 %Au solidifica dando lugar a un constituyente
eutéctico, formado por dos fases ( Bi y C), por lo que a la derecha del mismo que corresponde a
la aleación del 40 % de Au tendremos a temperatura ambiente como microconstituyentes el
eutéctico y el compuesto.
65.4 − 40
% eutéctico =
⋅100 = 48%
65.4 − 12.5
%C = 52%
11
Problemas de diagramas de equilibrio
e) Curvas de enfriamiento
900
L
Temperatura
800
65.4 %
Au
40 % Au
700
600
L + Au
L
500
400
371ºC
300
L + Au
241ºC
L + Au + C
L+C
L+C+Bi
200
L + Au + C
C
Bi + C
100
Tiempo
PROBLEMA 7
En el sistema de las aleaciones Pb - Au se producen las siguientes transformaciones:
-
A 418 ºC el oro reacciona con un liquido del 55 % Au para dar un compuesto definido
C1 con un contenido en Au del 65.6 %.
-
A 254 ºC el compuesto definido anteriormente reacciona con una fase liquida de un 28
% de Au para formar otro nuevo compuesto C2 con un contenido en Au del 32.2 %.
-
A 215 ºC un liquido con una composición del 15 % de Au reacciona transformandose
en dos fases sólidas que son el compuesto definido como C2 y el Pb puro.
Los puntos de fusión del Au y del Pb son, respectivamente, 1063 ºC y 327 ºC. Se pide:
a) Dibujar el diagrama binario indicando fases y definiendo lineas y puntos. NOTA:
Todas las lineas del diagrama se trazaran rectas.
b) Deducir las formulas de los compuestos definidos.
c) Relación entre las fases sólidas que se forman en la transformación que tiene lugar a
215 ºC.
DATOS :
12
PAu = 196,96 gr/mol
PPb = 207,2 gr/mol
Problemas de diagramas de equilibrio
a) Diagrama
1200
1000
diagrama Pb-Au
800
L
600
L+Au
400
200
Pb + L
L+C2
254 ºC
C2
215 ºC
Pb+C2
418 ºC
L+C1 C1
C2+C1
C1+Au
0
0
10 20 30 40 50 60 70 80 90 100
Pb
Au
b) Fórmulas de los compuestos
La formula del compuesto C1(34,4 %Pb - 65,6 %Au) será : Pbx Auy
masa de Pb =
x PPb
34.4
=
100 x PPb + y PAu
masa de Au =
y PAu
65.6
=
100 x PPb + y PAu
34.4 x PPb
=
65.6 y PAu
x 34.4 ⋅ 196.96
1
=
= 0 .5 =
y
65.6 ⋅ 207.2
2
⇒
Por tanto, los valores de x e y son: x = 1 y = 2. La fórmula del compuesto es: PbAu2
Llevando a cabo el mismo proceso para el compuesto C2 obtenemos :
67.8 x PPb
=
32.2 y PAu
⇒
x 67.8 ⋅196.96
=2
=
y
32.2 ⋅ 207.2
La formula del compuesto C2 será: Pb2 Au
13
Problemas de diagramas de equilibrio
c) Relación entre fases sólidas a 215 ºC
ºC
⎯⎯
→ Pb + C2 (32.2% Au )
A 215 ºC tiene lugar la transformación eutéctica: L(15% Au ) ⎯215
% C2 =
15 − 0
⋅100 = 46.6%
32.2 − 0
% Pb = 53.4%
PROBLEMA 8
Dado el diagrama Ag-Al: indicar las fases que aparecen en cada zona del diagrama,
nombrar y escribir la ecuación específica de las reacciones que se desarrollan en cada
linea horizontal.
1000
900
L
diagrama Ag-Al
+
800
α
L
700
α
L+δ
L+γ
600
γ
500
α
+
β
L+γ
γ
+
α
δ
γ +δ
400
β
α
+
θ
300
θ
γ
γ
+θ
200
0
10
20
30
40
50
60
14
80
90
100 0
Al
Ag
Peritéctica
Peritéctica
Eutéctica
70
L +α ⎯
⎯→ β
L+β ⎯
⎯→ γ
L ⎯
⎯→ γ + δ
Eutectoide
Peritectoide
4
8
Ag
β ⎯
⎯→ α + γ
α +γ ⎯
⎯→ θ
12
16
Al
Problemas de diagramas de equilibrio
PROBLEMA 9
Dado el diagrama Fe – Sn, se pide:
a) Indicar las fases presentes en las distintas zonas del diagrama.
b) Escribir las reacciones que se producen en T1...T6.
c) Dibujar la curva de enfriamiento de una aleación del 25 % de Fe.
d) ¿Que intervalo de temperaturas escogería para la forja de una aleación del 95 % de
Sn?
DATOS:
PFe = 55,8 gr/mol
PSn = 118,7 gr/mol
a) Fases
diagrama Fe-Sn
1600
L1
1400
α
+
γ
1200 γ
L1+α
1000
800
L2
L1+L2
T1
α + L2
T2
α
T4
600
ε + L2
T3
ε ε+η
α+ε
400
η
α+η
200
η + L2
T5
θ + L2
T6
η+θ
θ
θ + Sn
0
0
Fe
10
20
30
40
50
60
70
80
90
100
Sn
α y γ son soluciones sólidas primarias de Sn en Fe, formadas al insertarse Sn en las
variedades alotrópicas del Fe (α cúbica centrada y γ cúbica centrada en las caras).
15
Problemas de diagramas de equilibrio
b) Reacciones a T1..... T6
T1:
T2:
T3:
T4:
T5:
T6:
Monotéctica L1 ⎯
⎯→ α + L2
Peritéctica
α + L2 ⎯
⎯→ ε
Peritéctica
ε + L2 ⎯
⎯→ η
Eutéctoide
ε ⎯
⎯→ α + η
Peritéctica
η + L2 ⎯
⎯→ θ
R. isotérmica de solidificación del Sn puro
L2 (100% Sn)
⎯
⎯→ Sn
d) Curva de enfriamiento
L1 + L2
Temperatura
25 % Sn
L1 + α
T1
L2 + α
T2
α+ε
T4
α+η
Tiempo
d) ¿Que intervalo de temperaturas escogería para la forja de una aleación del 95 % de
Sn?
Elevaría la temperatura sin llegar a T6 puesto que por encima de ella se forma fase líquida.
16
Problemas de diagramas de equilibrio
PROBLEMA 10
El mercurio y el plomo se pueden combinar dando las siguientes fases: solución
sólida α que admite hasta el 1 % de Pb. a - 50 ºC, sol.sol. β que admite hasta el 22 % de
Hg. a 250 ºC y fase intermedia θ cuya composición en Pb puede oscilar entre 65-70 %.
Esta fase funde incongruentemente a 250 ºC dando sólido β y líquido de composición 40
% Pb.
50 º C
El sistema presenta otra reacción invariante:
L (5% Pb) ⎯−⎯
⎯→ α (1% Pb) + θ
Se conoce además que la solubilidad del Hg en Pb no varia con la temperatura. Se pide:
a) Dibujar el diagrama y asignar las fases.
b) Fórmula que se puede dar a la fase θ y tipo de fase intermedia que es.
c) Análisis de fases de una aleación del 25 % de Hg a 252 ºC y a 248 ºC.
d) Indicar la aleación de más bajo punto de fusión y la aleación más rica en Hg que sea
sólida a 25 ºC.
DATOS:
Hg: Tf = -38 ºC ; PHg = 200,6 gr/mol
Pb: Tf = 325 ºC ; PPb = 207 gr/mol
a) Dibujar el diagrama y asignar las fases.
400
diagrama Hg-Pb
L+β
300
250
200
θ+β
L
L+θ
100
α
0
β
L+α
α+β
-100
0
10
Hg
20
30
40
θ
-50 ºC
50
60
70
80
90
100
Pb
b) Fórmula que se puede dar a la fase θ y tipo de fase intermedia que es.
17
Problemas de diagramas de equilibrio
Considerando una composicion media del 67,5 % de Pb. La fórmula del compuesto será: Pbx
Hgy
masa de Pb =
x PPb
67.5
=
100 x PPb + y PHg
masa de Hg =
y PHg
32.5
=
100 x PPb + y PHg
67.5 x PPb
=
32.5 y PHg
⇒
x
67.5 ⋅ 200.6
≈2
=
y
32.5 ⋅ 207
Por tanto, los valores de x e y son: x = 2 y = 1. La fórmula del compuesto es: Pb2 Hg
c) Análisis de fases de una aleación del 25 % de Hg (75% Pb) a 252 ºC y a 248 ºC.
β = 22 % Hg L = 60 % Hg
A 252 ºC:
%L =
A 248 ºC:
%β =
25 − 22
⋅100 = 7.89% y
60 − 22
β = 22 % Hg y
%β =
60 − 25
⋅ 100 = 92.11%
60 − 22
θ = 32,5 % Hg
25 − 22
⋅ 100 = 28.57%
32.5 − 22
y
%θ =
32.5 − 25
⋅ 100 = 71.43%
32.5 − 22
d) Indicar la aleación de más bajo punto de fusión y la aleación más rica en Hg que sea
sólida a 25 ºC.
La aleación de más bajo punto de fusión es la eutéctica, con un 5 % de Pb.
La más rica en Hg, a 25 ºC, es la α, con un contenido mínimo de Hg del 99 %.
18