Unidad 6: Geometría del espacio y medición II. Sólidos geométricos

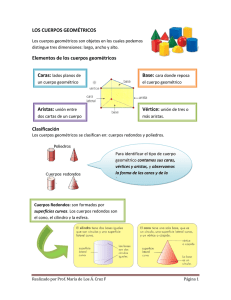
Unidad 6: Geometría del espacio y medición
II. Sólidos geométricos
1. Identificar los sólidos geométricos
SÓLIDOS GEOMÉTRICOS
Los sólidos geométricos son figuras del espacio que tienen tres
dimensiones (largo, ancho, alto) que consiste en todos los puntos de su
superficie más todos los puntos de sus interiores. Algunas superficies
de los sólidos son planas o caras. Los sólidos con todas las superficies
planas que ocupan una región simple en el espacio son llamados
poliedros.
Existen diferentes poliedros entre ellos:

Prisma: es un poliedro con dos caras congruentes que son
polígonos contenidos en planos paralelos.
o Estas dos caras se llaman bases del prisma.
 Si las bases son polígonos regulares se llaman
prismas regulares. Los prismas reciben su nombre
de acuerdo a la forma de las bases. Algunos de
ellos son:
 Cubo: es un prisma que todas sus caras son
cuadrados.

Prisma triangular: sus bases son triángulos.

Prisma recto o rectangular: sus bases son
rectángulos.

Prisma pentagonal: sus bases son pentágonos.
o Las otras caras se llaman caras laterales y son
paralelogramos.
 Paralelogramo: es un cuadrilátero (polígono de 4
lados) cuyos pares de lados opuestos son paralelos.

Pirámide: es un poliedro donde todas las caras, excepto una
cara, se intersecan en un punto llamado vértice.
o La cara que no contiene el vértice se llama base y es una
región poligonal. Puede ser un rectángulo, pentágono, etc.
o Las caras que se intersecan en el vértice se llaman caras
laterales y son regiones triangulares.

Poliedros regulares: es un sólido geométrico que tiene todas sus
caras en forma de polígonos regulares congruentes.
o Existen exactamente cinco clases de poliedros regulares
llamados sólidos platónicos, puesto que Platón los
describió por completo en sus escritos.
 Tetraedro: tiene 4 caras y sus caras triangulares,
encontrándose tres de ellas en cada vértice. Si las
cuatro caras del tetraedro son triángulos
equiláteros, forzosamente iguales entre sí, el
tetraedro se denomina regular.

Hexaedro: tiene 6 caras y sus caras han de ser
polígonos de cinco lados o menos. Si las seis caras
del hexaedro son cuadrados congruentes, el
hexaedro se denomina regular conocido como cubo.

Octaedro: tiene 8 caras y sus caras han de ser
polígonos de siete lados o menos. Si las ocho caras
del octaedro son triángulos equiláteros se denomina
regular.

Dodecaedro: tiene 12 caras y sus caras han de ser
polígonos de once lados o menos. Si las doce caras
del dodecaedro son pentágonos regulares,
forzosamente iguales entre sí, el dodecaedro se
denomina regular

Icosaedro: tiene 20 caras y sus caras han de ser
polígonos de diecinueve lados o menos. Si las veinte
caras del icosaedro son triángulos equiláteros,
forzosamente iguales entre sí, el icosaedro se
denomina regular.
Existen otros sólidos que no son poliedros porque sus bases no
son polígonos sino que regiones circulares, como:
 cilindro: es un sólido con sus bases en un par de planos
paralelos y circulares.

Cono: tiene una base circular y un vértice.

Esfera: es un conjunto de puntos en el espacio cuya
distancia a un punto dado es conocida (radio).
Ejemplo: Determina que formas representan un poliedro.
No poliedro
Es cilindro
Sí, poliedro,
Pirámide
Sí, poliedro,
Prisma octagonal
No, poliedro
Es cono