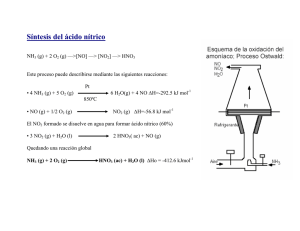
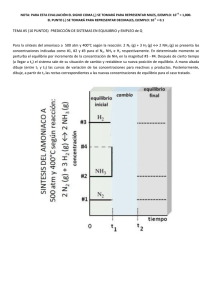
Balance de Materia con Reacción Química Previo a introducirnos en
Anuncio

Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Balance de Materia con Reacción Química Previo a introducirnos en el tema vamos a recordar (y aprender) conceptos básicos relacionados a las reacciones químicas. 1) Estequiometría: Se refiere a la proporción en que se combinan ciertos reactivos para dar los productos. Ej: 2A + B → C + 3D Significa: 2 mol de A + 1 mol B → 1 mol C + 3 mol D O sea que la relación estequiométrica: mol A/mol B = 2, es decir, siempre será necesario el doble de moles de A que de B para que se produzca la reacción. Cociente estequiométrico: mol A/ mol B = relación de coeficientes estequiométricos. Coeficiente estequiométrico: es el nº mínimo de moles de 1 especie dada que debe ponerse en juego en una reacción química para asegurar el balance atómico. Los números que preceden a cada especie molecular son los coef. estequiométicos y los denominamos con la letra griega ν, o sea el coef. Esteq. de A → ν A= 2 Otra lectura de la ecuación estequiométrica referida los productos es: se consumen 2 mol de A para producir 3 mol de D. 2) Conversión (α) : Ya hemos visto en Química General que una reacción química no necesariamente se produce en un instante y también que no necesariamente se produce en su totalidad; es decir que no desaparecen totalmente los reactivos y sólo obtengo productos al terminar la reacción. En otras palabras, no es práctico diseñar un reactor que consuma totalmente los reactivos. Definimos entonces conversión como: moles consumidos moles suministrados N iE N iS N iE α. 100 = porcentaje de conversión Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT 3. Exceso: Recordemos el concepto de reactivo limitante: es el reactivo que desaparece cuando se lleva a cabo una reacción. Ej: 2A + B → C + 3D Ingreso: 200 moles A + 150 moles B Podemos ver que en caso que la reacción se produzca totalmente se consumirá todo el A y sobrarán 50 moles de B. O sea A es el reactivo limitante. El o los reactivos que no son limitantes (en este caso, B) se conoce como reactivo en exceso . Definimos entonces Exceso como: moles que ingresan moles teóricos moles teóricos Ex En nuestro caso: Ex (B) = (150 – 100)/100 = 0,5 Ex * 100 = 50% (porcentaje de exceso) 4. Grado de Avance (ξ) : Es una medida de la extensión en que se ha completado la reacción química consumiendo los reactivos. Es una variable dimensional, cuyas unidades pueden ser: mol, lbmol, etc. Veamos un ejemplo: Ejemplo 11 2A + B → C + 3D Supongamos que parto de proporciones estequiométricas de reactivos y a la salida del reactor tengo los siguientes resultados: 200 mol A 100 mol B 1 50 mol C 150 mol D 50 mol B 100 mol A 2 R Qué pasó? De B sólo han reaccionado 50 mol, ya que quedaron 50 mol sin reaccionar. Esto quiere decir que la reacción avanzó sólo 50 mol de B (se consumieron 50 mol B; y si miro a A sólo 100 mol de A (νA.50= 2. 50= 100 mol A). El grado de avance de esta reacción es: ξ = 50 mol. Veamos cómo escribir esto matemáticamente, usando la estructura de balance: n1B nB2 → n1B nB2 0 Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT n1A n A2 → n1A n A2 2 2 nC2 nD2 → nC2 → nD2 3 0 0 3 0 Veo ahora: Entra – Sale + Genera = 0 Genera = ν i. ξ Donde: ν i <0 si es de reactivos (consume (-): Sale del sistema) ν i >0 si es de productos (produce (+): Ingresa del sistema) Obviamente tendremos tantos ξ como reacciones químicas. Conversión: Dado el siguiente esquema, definimos: A B 1 M A B C D 2 R A B C D Conversión por paso: A B C D 4 αA (por paso) = αA (global) = Conversión global: 3 n A2 n 3A n A2 n1A n 3A n1A Balances atómicos: Nos pongamos de acuerdo: SIEMPRE LA MASA ES CONSTANTE. Sin reacción química: se conservan las moléculas (las especies moleculares no cambian) Con reacción química: se conservan los átomos, desaparecen especies moleculares (reactivos) y aparecen nuevas (productos). Veamos un ejemplo: Ejemplo 12 N2. 20% H2. 70% NH3. 10% 1 R 2 1 N2 H2 NH3. 57% Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT El cambio en el % de NH3 se debe a la reacción química que se produce. Hagamos los balances atómicos: Átomos N) N sale – N entra = 0 N sale = 2. N2)2 + 1. NH3)2 N entra = 2. N2)1 + 1. NH3)1 N sale – N entra = 2. N2)2 + 1. NH3)2 – (2. N2)1 + 1. NH3)1)= 0 = 2. [N2)2– N2)1] + 1.[NH3)2- NH3)1] = 0 N2 N sale – N entra = 2. N2 + 1. NH3 = 0 NH3 → - 2. N2 = 1. NH3 Átomos H) H sale – H entra = 0 NH 3 2 Hsale=2. H2)2 + 3. NH3)2 N2 1 H2 3 H entra = 2. H2)1 + 3. NH3)1 H sale – H entra = 2. H2 + 3. NH3 = 0 → - 2. = 3. NH3 2 Sistema lineal homogéneo indeterminado, por lo tanto cualquiera de los incrementos puede ser desplazado al 2º miembro como término independiente. Puedo escribir: N2 NH 3 2 H2 3 NH 3 2 Tengo 2 ecuaciones con 3 incógnitas; por lo tanto tengo una variable independiente. NH 3 2 N2 1 H2 3 Los denominadores son los coeficientes esteq. νi de la ecuación química que los combina, y que me permite relacionar los moles. 1 N2 + 3 H2 → 2 NH3 Esta ecuación resume la solución del balance atómico. Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Desde el punto de vista del balance, los coeficientes estequiométricos de los reactivos son negativos. Observemos que los incrementos moleculares son directamente proporcionales a sus coeficientes estequiométricos y del mismo signo en una misma reacción. Grado de avance: para desacoplar los incrementos moleculares y manejarlos por separado se introduce el concepto de GRADO DE AVANCE ξ (psi) de la reacciónVeamos del ejemplo anterior: NH 3 2 N2 1 H2 " valor común" 3 ni i Este “valor común” se denomina grado de avance y mide el número de veces que la reacción produce o consume (genera) una cantidad estequiométrica de moles de c/u de los productos y reactivos respectivamente. Generalizando escribimos que: ni i → ni Si ξ< 0, indica que la reacción se está produciendo al i. revés. Recordar: Incremento: cantidad final – cantidad inicial νi de los reactivos es < 0. Estructura del término Generación. Vemos ahora que: ni = [ Sale(i) – Entra (i)] = Genera (i) = νi.ξ Genera (i) = νi.ξ Molar: νi.ξ Másico: νi.ξ.PMi Si en un sistema se produce más de 1 reacción química, c/u tendrá su propio ξ. Si una especie molecular (i) participa en más de una reacción dentro del sistema, su incremento ni resultará de sumar los incrementos parciales que produce cada reacción en la que participa. ni = = νi1.ξ1 + νi2.ξ2 +….+ νin.ξn= n ir . r r 1 El problema de cuantificar los incrementos moleculares ni se reduce a determinar los grados de avance ξ r de cada una de las reacciones químicas dentro del sistema. Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Veamos ahora el siguiente ejemplo: Ejemplo 13 N2 O2 NH3 N2 O2 R 1 2 1 NH3 H2O NO2 Desconocemos cuantas reacciones químicas se producen. Hagamos los balances atómicos: N) 1. NH3 + 2. N2 + 1. NO2 = 0 Sistema lineal homogéneo indeterminado: H) 3. NH3 + 2. H2O = 0 3 ecuaciones de balance y 5 incógnitas O) 2. O2 + 1. H2O + 2. NO2 = 0 → tengo 2 variables independientes. Elijo variables independientes: NH3 y . NO2 Entonces: 2 N2 = - NH3 - NO2 2) 2. H2O = - 3. NH3 3) 2. O2 + 1. H2O = - 2. 1) Reemplazo 2) en 3) O2 2 N2 = - NH3 - NO2 2. O2 = 3/2. NH3 - 2. 2. H2O = - 3. NH3 → O2 → → N2 = -1/2. NH3- 1/2. NO2 O2 = 3/4. NH3 O2 H2O = - 3/2. NH3 Observo ahora las ecuaciones fijándome en 1 de las variables independientes NH3; queda entonces: N2 NH 3 2 O2 3 NH 3 4 H 2O 3 NH 3 2 NH 3 2 N2 1 O2 3 2 H 2O 3 1 Coeficientes estequiométricos Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Por lo tanto: 2 NH3 + 3/2 O2 → N2 + 3 H2O Veamos ahora la otra variable independiente N2 NO2 2 O2 1 NO 2 1 NO2 2 N2 1 O2 2 A O2 2 Coeficientes estequiométricos Por lo tanto: N2 + 2 O2 →2 NO2 B Estas relaciones (A y B) definen 2 ecuaciones estequiométricas Obtengo 2 reacciones químicas independientes: IGUAL Nº de REACCIONES QUIMICAS QUE VARIABLES INDEPENDIENTES. Las variables independientes no pueden estar nunca en la misma reacción!!! Veamos ahora qué pasa si tomo como variables independientes N2 y O2. Antes de efectuar ningún procedimiento matemático observamos, en función de las entradas y salidas del reactor, que necesariamente debe existir 1 reacción que involucre al O2 y al N2, Por lo tanto no se cumpliría que las variables independientes no pueden estar nunca en 1 misma reacción (sería lo mismo si tomo NH3 y H2O; o O2 y H2O). Ver balances atómicos. Tomemos entonces como variables independientes N2 y NH3. Entonces: 2 N2 = - NH3 - NO2 2) 2. H2O = - 3. NH3 derecho 3) 2. O2 + 1. H2O = - 2. 1) 1) NO2 N2 1/ 2 las reordeno dejando las var. indep en el lado O2 NH 3 1 Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT 2) H 2O 3) O2 NH 3 2/3 NO2 1 H 2O 2 Reemplazo en 3, 2 y 1: ( O2 NH 3 ) 1 N2 1/ 2 ( 1 NH 3 ) 2/3 2 N2 1/ 2 NH 3 .(1 3 / 4) NH 3 4/7 N2 1/ 2 Queda entonces: NH 3 1 N2 1/ 2 1) NO2 2) H 2O 3) O2 NH 3 1 NH 3 2/3 N2 1/ 2 NO2 1 N2 1/ 2 H 2O 3/ 2 NO2 1 O2 1 O2 7/4 1 * 2 NH 3 4/7 * Como el agua no puede tener coeficiente fraccionario, multiplico por 2, el denominador de la 1º ecuación: 2 NH3 + 7/2 O2 → 2 NO2 + 3 H2O N2 + 2 O2 → 2 NO2 D C → idéntica la encontrada anteriormente Ec. B Veamos ahora si tomamos como variables independientes N2 y NO2. 1) NH 3 NO2 1 2) H 2O NH 3 2/3 3) O2 NO2 1 N2 1/ 2 H 2O 2 Reemplazando 1) y 2) en 3): Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT NO 2 1 O2 NO 2 1 3 4 Queda entonces: NO2 1) NH 3 1 2) H 2O 3) O2 N2 1/ 2 7 . NO 2 4 3 . N2 2 NO 2 4/7 N2 2/3 N2 1/ 2 NO2 2/3 N2 1/ 3 NO2 4/7 N2 2/3 Si ∆NO2 = 2 → ∆NH3 = -2 → ∆H2O = 3 → ∆O2 = -7/2 2NH3 + 7/2 O2 → 2 NO2 + 3 H2O E Si ∆N2 = 1 → ∆NH3 = -2 → ∆H2O = 3 → ∆O2 = -3/2 2NH3 + 3/2 O2 → N2 + 3 H2O F Observamos que: A = F B = D C = E Podemos concluir entonces: El sistema involucra 2 reacciones químicas: tantas reacciones químicas como especies moleculares independientes haya en el balance atómico. Las 2 reacciones pueden elegirse de cualquier modo y escribirse en cualquier sentido. La única condición es que intervengan todas las especies reactivas. Cualquier combinación lineal que mantenga el nº correcto de ecuaciones estequiométricas es otra solución válida para el balance atómicoNo es posible fusionar las ecuaciones esteq. en una sola porque se crean proporciones forzosas (arbitrarias) entre los incrementos. La solución correcta del balance depende del nº de ecuaciones esteq., pero no de cuáles sean estas ecuaciones. Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Por lo tanto, de ahora en más, trabajaremos con ecs. esteq. y tendremos siempre en cuenta que: nº reacciones químicas = nº especies moleculares – nº especies atómicas Cada reacción química incrementa una incógnita: su grado de avance; por lo que ahora el nº de ecuaciones de balance disponibles para compensar los pesos será: nº ecuaciones de balance = nº especies moleculares - nº reacciones químicas O lo que es lo mismo: nº ecuaciones de balance = nº especies atómicas Volvamos al Ejemplo 12: N2. 20% H2. 70% NH3. 10% R 1 2 1 2 1 2 N2 H2 NH3. 57% 222 nº reacciones químicas = nº especies moleculares – nº especies atómicas nº reacciones químicas = 3 – 2 = 1 nº ecuaciones de balance = nº especies moleculares - nº reacciones químicas nº ecuaciones de balance = 3 – 1 = 2; o bien: nº ecuaciones de balance = nº especies atómicas nº ecuaciones de balance = 2 GL = 3 -2 = 1 – Base = 0 N2 + 3 H2 = 2 NH3 ξ NH3) 0,10.F1-0,57.F2 + 2 ξ = 0 1 N2) 0,20.F1 – XN2. F2 - ξ = 0 2 H2) 0,70.F1 – XH2. F2 – 3 ξ = 0 3 Σ = F1 – F2 = 2 ξ = - Σ νi.. ξ 4 ∆ nº moles = F2 - F1 = Σ νi.. ξ Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Base: F1 = 100 moles/h Reemplazo en 4): 100 – F2 - 2 ξ = 0 → F2 = 100 - 2 ξ Reemplazo en 1): 10 – 0,57 .F2 + 2 ξ = 0 10 – 0,57 .(100 - 2 ξ ) + 2 ξ = 0 10 – 57 + 1,14. ξ + 2 ξ = 0 → ξ = 47/3,14 → ξ = 15 mol/h F2 = 100 - 2 (15) → F2 = 70 mol/h XN2 = (0,20.100 –15 )/70 → XN2 = 5/70 → XN2= 0,0714 XH2= (0,70.100 – 3. 15)/70 → XH2 = 35/70 → XH2= 0,3571 Se podría calcular también como: XNH3 + XN2 + XH2=1→ XH2= 1- 0,57 – 0,0714→ XH2 = 0,3586 Síntesis para resolver los balances de materia con reacción química: Formular Balances Atómicos Sustituir las variables del problema Resolución matemática PROBLEMA Estructurar las ecuaciones estequiométricas uiometricas Formular Balances Moleculares Sustituir las variables del problema Calcular ξ Veamos el otro ejemplo: Ejemplo 13 N2 30% O2 50% NH3 20% R 1 1 2 1 3 N2 O2 NH3 9% H2O NO2 15% % molares nº reacciones = nº especies moleculares – nº especies atómicas = 5 – 3 = 2 nº ecuaciones = nº especies moleculares – nº reacciones = 5 – 2 = 3; o bien: Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT nº ecuaciones = nº especies atómicas = 3 GL = 4 – 3 = 1 – Base = 0 Reacciones: 2NH3 + 3/2 O2 → N2 + 3 H2O ξ1 N2 + 2 O2 → 2 NO2 ξ2 Balances: NH3) 0,2.F1 -0,09.F2 -2 ξ1= 0 N2) 0,3.F1 – XN2.F2 - ξ2 + ξ1= 0 O2) 0,5.F1 – XO2.F2 -3/2.ξ1- 2.ξ2 = 0 NO2) -0,15.F2 + 2.ξ2 = 0 H2O) – XH2O.F2 +3 ξ1= 0 Analizando veo que conviene poner la base en la corriente 2: F2 = 100 mol/h de NO2) ξ2 = 15/2 → ξ2 = 7,5 mol/h BT) F1 – F2 +1/2. ξ1- ξ2= 0 F1 – 100 + 1/2. ξ1- 7,5 = 0 → F1 = 107,5 -1/2. ξ1 NH3) 0,2.F1 -0,09.100 -2 ξ1= 0 → F1 = 9/0,2 + (2/0,2). → F1 = 45 + 10. ξ1 Igualando ambas ecuaciones: 107,5 -1/2. ξ1= 45 + 10. ξ1→ ξ1= 62,5/10,5→ ξ1= 5,952 mol/h F1 = 45 + 10. (5,952)→ F1 = 104,52 mol/h XH2O =3 ξ1/F2 → XH2O = 3. (5,952/100) → XH2O =0,1786 XN2 =(0,3.F1 - ξ2 + ξ1)/ F2→ XN2 =(0,3. 104,52 – 7,5 + 5,952)/100 → XN2 = 0,298 XO2= 1 - XN2 - XH2O – XNH3 – XNO2 = 1 – 0,298 – 0,1786 – 0,09 -0,15 → XO2= 0,2834 Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Reactor incluido en una “Caja Negra” Veamos el siguiente ejemplo: Ejemplo 14 D-72,73% (en peso) C-27,27% 6 1 A B 2 M 1 3 A B C 2 R 3 2 (en peso) A- 20,98% B – 12,91% C D D 2 3 4 A B C A B C 5 1 1 4 B A-49,6% (en peso) B C 2 1 7 Ecuación complementaria: F5 F4 2 3 Reacciones químicas: A+B→2C ξ1 A+C→D ξ2 PMA = 60 g/mol PMB = 40 g/mol Por Lavoisier: PMC = 50 g/mol PMD = 110 g/mol Calcular: 1- Composición de corriente 1 2- Conversión global de A 3- Conversión por paso de B Análisis de GL: Σ pesos = 12 Σ ecuaciones = 10 + 1 = 11 GL = 12 – 11 = 1 – 1 base = 0 Veamos por equipo: Destilador: GL = 5 - 4 = 1 – base = 0 Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Base: G3 = 100 g/h A) 20,98 – 0,496.G4 = 0 → G4 = 20,98/0,496→ G4 = 42,3 g/h BT) G3 = G6 + G4 → G6 = G3 – G4 = 100 – 42,3 → G6 = 57,5 g/h B) 12,91 – wB)4. G4 = 0 → wB)4= 12,91/42,3→ wB)4= 0,305 Σwi)4 =1 → wC)4= 1 - wA)4- wB)4 = 1 – 0,496 – 0,305 → wC)4= 0,199 = 0,2 wi)4 = wi)5 = wi)7 Para poder usar la ecuación complementaria: F4 wi .G4 PM i F4 wA 4 PM A wB 4 PM B wC 4 .G4 PM C F4 0,496 60 0,305 40 0,2 .42,3 50 F5 F4 2 , debo calcular los flujos molares: 3 wi G4 PM i F4 = 0,84 mol/h F5 = (2/3). F4 → F5 = 0,56 mol/h F5 G5 wA 5 PM A wB 5 PM B 0,56 0,496 0,305 60 40 wC 5 .G5 PM C G5 wA 5 PM A F5 wB 5 PM B wC 5 PM C 0,2 50 G5 = 28,15 g/h Bifurcador: BT) G4 = G5 + G7 → G7= G4 – G5 = 42,3 – 28,15 → G7= 14,15 g/h Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz Introducción a la Ingeniería Química Dpto. de Ingeniería de Procesos y Gestión Industrial FACET - UNT Caja Negra G6 = 57,5 g/h D-72,73% (en peso) C-27,27% 6 1 G1 A B CN 7 G7 = 14,15 g/h A-49,6 % (en peso) B-30,5 % C-20 % BT) G1 = G6 + G7 = 57,5 + 14,15 → G1 = 71,65 g/h D) -0,7273.G6 + ξ2. PMD = 0 → ξ2= 0,7273. 57,5/110 → ξ2= 0,38 mol/h A) -0,2727. G6 – 0,20. G7 + 2 ξ1. PMC - ξ2. PMC = 0 ξ1= (0,2727. 57,5 +0,20.14,15+0,38.50)/(2.50) → ξ1= 0,375 mol/h A) wA1.G1 -0,496.G7 –(ξ1 + ξ2).PMA = 0 → wA1=(0,496.14,15 +(0,38+0,375).60)/71,65 → wA1= 0,73; → wB1= 0,27 Conversión global de A: αA = (NA1 – NA7)/NA1= (ξ1 + ξ2)/NA1= (ξ1 + ξ2)/(wA1.G1/PMA) αA = (0,38 +0,375)/(0,73.71,65/60) → αA = 0,866 Conversión por paso de B: αB = (NB2 – NB7)/NB2= ξ1/NB2 Mezclador: A) (wB1.G1 + wB5.G5)/PM B = NB2 →NB2= (0,2727.71,65+0,3.28,15)/40 → NB2= 0,7 αB = 0,375/0,70 → αB = 0,536 Ing. Carlos Correa, Dra. Norma Barnes, Dra. Dora Paz