Presentación de la práctica 4

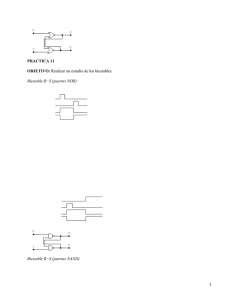
Práctica 4:
CONTADORES
1
Introducción
Biestables
Son circuitos que tienen dos estados estables. Cada estado puede
permanecer de forma indefinida. Son circuitos con memoria
Clasificación:
• Asíncronos: no necesitan señal de sincronización para cambiar la
salida
• Síncronos: necesitan una señal para validar la salida (Señal de
sincronismo o de reloj CLK)
Asíncronos à R–S
Síncronos à R–S, J-K, T, D
2
Circuitos secuenciales asíncronos
Con puertas NOR
Biestables R-S
R
R
Q
S
Q
Q
Q
R
S
Qt
0
0
Qt-1
0
1
1
1
0
0
1
1
Prohibido
No S
cambia
de
estado
Con puertas NAND
S
Q
Q
R
3
Circuitos secuenciales asíncronos
Utilizar biestables síncronos
Presencia de glitches
Aparecen problemas en los sistemas asíncronos cuando aparecen
transitorios de la señal de entrada que son capturados a la entrada
de los biestables
’0’
’1’
’1’
tp
tp
A’
R
tp
S
A
B
A B
Q
tp
.....
Q
R
S
Qt
0
0
Qt-1
0
1
1
1
0
0
1
1
Prohibido
2tp
A’ S
t0
4
Circuitos secuenciales síncronos
Nomenclatura de la señal de reloj
Biestables tipo LATCH
Nivel alto
CLK
Nivel bajo
CLK
Biestables tipo FLIP-FLOP
Flanco de subida
CLK
Flanco de bajada
CLK
5
Circuitos secuenciales síncronos
Biestables R-S síncronos
S (SET) es la puesta a 1 y R (RESET) es la puesta a 0 del biestable. Si
las entradas S y R están a 1 la salida valdrá 0 o 1. Si R y S son 0 no
cambia el estado
CLK
R
Q
CLK
S
Q
Señal de reloj
(Flanco descendente)
R
S
Qt
x
x
Qt-1
0
0
Qt-1
0
1
1
1
0
0
1
1
0 (B.P.)
1 (I.P.)
Biestable R-S activo
por flanco de bajada
6
Circuitos secuenciales síncronos
Biestables J-K
Resuelve el problema de la prohibición del estado R=S=1 del
biestable R-S. J es la puesta a 1 y K es la puesta a 0 del biestable. Si
las entradas J y K están a 1 la salida cambia su estado. Si J y K son 0
no cambia el estado
CLK
J
Q
CLK
K
Q
J
K
Qt
x
x
Qt-1
0
0
Qt-1
0
1
0
1
0
1
1
1
Qt-1
Biestable J-K activo
por flanco de bajada
7
Circuitos secuenciales síncronos
Biestables J-K síncronos con entradas asíncronas de preset y clear
Los dispositivos comerciales suelen disponer de unas entradas asíncronas
para la puesta a cero del biestable (Clear) y para su puesta a uno (Preset)
CLK
Preset
J
Q
J
K
Qt
x
x
Qt-1
0
0
Qt-1
0
1
0
1
0
1
1
1
Qt-1
CLK
K
Q
Clear
Preset
Clear
Qt
0
0
Prohibido
0
1
1
1
0
0
1
1
Qt-1
Con Clear = Preset = ‘1’ tenemos el funcionamiento normal del biestable
8
Circuitos secuenciales síncronos
Biestables T
La salida del biestable cambia de estado siguiendo la evolución de
la señal T. El biestable T es la base de los contadores asíncronos.
T
CLK
CLK
Q
T
Qt
0
Qt-1
1
Qt-1
9
Circuitos secuenciales síncronos
Biestables T
No existe comercialmente y se consigue con biestables tipo J–K.
Si conectamos la entradas J y K y la denominamos entrada T
tendremos un biestable tipo T
T
CLK
J
Q
CLK
K
J
K
Qt
0
0
Qt-1
0
1
0
1
0
1
1
1
Qt-1
10
Circuitos secuenciales síncronos
Biestables D FLIP-FLOP
Pasa el valor presente
en la entrada D a la
salida cuando llega el
flanco descendente de
la entrada de reloj.
D
Q
CLK
D
Qt
X
Qt-1
1
1
0
0
CLK
D
Qt
0
X
Qt-1
1
1
1
1
0
0
CLK
Q
Biestables D LATCH
Pasa el valor presente
en la entrada D a la
salida cuando tenemos
un nivel alto en la
entrada de sincronismo.
D
Q
CLK
Q
¡ Activo por nivel !
11
Circuitos secuenciales síncronos
Utilizar configuración master-slave
Problema de las carreras
Problema que surge cuando existe realimentación de la salida
hacia la entrada del sistema cuando aún está activa la señal de
reloj
’1’
D
Q
CLK
Q
12
Circuitos secuenciales síncronos
Biestables Maestro-Esclavo (Master-Slave)
Corresponde a dos biestables (J-K ó R-S) dispuestos en serie (uno
maestro y el otro esclavo). Reciben esta denominación porque el
estado del biestable esclavo - una vez que el reloj de éste asi lo
permite - corresponde al estado de las salidas del biestable
maestro.
Para eliminar finalmente los problemas de carrera se usan con
configuración activos por flanco.
J
Q1
CLK
J
Q1
K
Q2
CLK
K
Q1
13
Aplicaciones de biestables
Contadores asíncronos
Tienen una entrada de reloj genérica y n salidas binarias que
representan en cada momento el valor en binario de los pulsos
que entran por la entrada de reloj. Los biestables no cambian al
mismo tiempo
Divisores de frecuencia
En muchas ocasiones la frecuencia de una señal no es la
requerida para la aplicación y se hace necesario dividir la
misma
Temporizadores
Las aplicaciones de los temporizadores en aplicaciones de
electrónica digital son imprescindibles.
14
Aplicaciones de biestables
Contadores asíncronos
Están basados en biestable de tipo T encadenados en cascada. Cada
vez que en la entrada de un biestable tipo T aparece un flanco
descendente (cambio de 1 a 0) el biestable cambia de estado
CLK
T Q
T Q
Q0
T Q
Q1
T Q
Q2
Q3
15
Aplicaciones de biestables
Contadores asíncronos
Cronograma
CLK
Q0
Q1
Q2
Q3
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 1
2
1
0 1
0 1
0 1 0 1
0 1
0 1
0 1
0 1
0
0 0
1 1
0 0
1 1
0 0
1 1
0 0 1 1
0
0 0 0 0
1 1 1 1
0
1 1 1 1 1 1
0
0 0 0 0
0 0
0
1
0 0
1 1 1
0 0 0 1 1
16
Aplicaciones de biestables
Contadores decimales
Para construir un contador decimal, utilizaremos un contador
binario de 4 bits y lo reseteamos (poner a cero) cuando entren 10
pulsos. Reseteamos el contador cuando tenemos la combinación
binaria de 10 (1010)
CLK
R
T Q
R
T Q
Q0
R
T Q
R
T Q
Q1
Q2
Q3
17
Aplicaciones de biestables
Contadores decimales
Reset con la
combinación 1010
CLK
R
CLK
Q0
BCD
Q1 Q2
Q0
Q3
Q1
Q2
Q3
8 9 10 1 2 3 4 5 6 7 8
1 0 1 0 1 0 1 0 1 0 1
1 0 0 0 0 1 1 0 0 1 1
1 0 0 0 0 0 0 1 1 1 1
0 1 1 0 0 0 0 0 0 0 0
Representación en diagrama
de bloques del contador
decimal (BCD)
18
Aplicaciones de biestables
Contador Ascendente-Descendente
CLK
T Q
T Q
T Q
T Q
A/D
Q0
Q1
Q2
Q3
• Con un 0 contador ascendente pasa a la salida el mismo número
que en la salida del biestable (salida Q)
• Con un 1 contador complementa el número que tenga la salida del
biestable ( salida Q (negada))
19
Aplicaciones de biestables
Divisor de frecuencia
Las salidas de un contador se pueden utilizar como un divisor de
frecuencia. Tal y como puede verse en el cronograma la frecuencia de
salida de cada salida divide por 2 la frecuencia de la anterior
CLK
1 2 3 4 5 6 7 8
fCLK
Q0 f
0 0 1
Q1
Q2
Q3
9 10 11 12 13 14 15 16
0 1 0 1 0 1 0 1
0 1
0 1
0 1
0 0
1 1
0 0
1 1
f1
0 0
f2
0 0 0 0
f3
0 0
1 1
0
0 0
1
0 0
1 1
1 1 1
0 0 0 0
0 0 0 1 1
fn =
fCLK
2 n +1
1 1 1 1
1 1 1 1 1 1
20
Aplicaciones de biestables
Divisor de frecuencia
R
CLK
Q0
Binario
Q1 Q2
R
CLK
Q3
fCLK fCLK fCLK fCLK
22 23 2 4
2
Q0
BCD
Q1 Q2
Q3
fCLK fCLK fCLK fCLK
2 2 2 3 10
2
Cuando el contador es de tipo BCD la salida Q3 no cumple la regla
fCLK/2n+1, sino que divide por 10 ya que cuando entran 10 pulsos se
resetea
21
Aplicaciones de biestables
Temporizador
El temporizador básico cuando detecta la combinación de
temporización y efectúa un cambio de 0 a 1.
VCC
Contador
Pulsador de
Inicio de
temporización
Combinacional
22
Aplicaciones de biestables
VCC
Pulsador de
Inicio de
Temporizador
temporización
R
CLK
Q0
CLK
1 2
3 4
5 6
Pulsador Inicio
Q
7 8
9
BCD
Q1 Q2
Q3
R
Q
S
23