Capítulo 3 – Cálculo proposicional 3.1

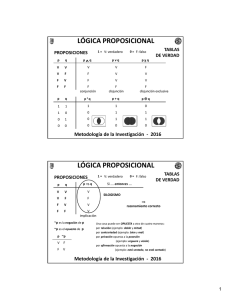
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería Informática
Capítulo 3 – Cálculo proposicional
3.2 - Proposiciones
El cálculo proposicional es el estudio de las relaciones lógicas entre objetos
llamados proposiciones, que frecuentemente pueden interpretarse como
afirmaciones que tienen algún significado en contextos de la vida real.
3.2 - Proposiciones
Una proposición es cualquier frase que tenga un valor de verdad bien
definido, es decir, que sea verdadera o falsa.
Proposiciones
No son Proposiciones
9Chile está en Asia
92 por 2 es igual a 4
9El color de ese auto es rojo
9Está lloviendo
9Francia está en Europa
9Inserte el CD
9¿Qué día es hoy?
9¿Dónde estoy?
9Socorro!!!
9Ir directamente a la cárcel
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería Informática
Capítulo 3 – Cálculo proposicional
En el cálculo proposicional se utilizan letras minúsculas p,q,r,s… para
simbolizar proposiciones, las que se combinan para obtener proposiciones
compuestas utilizando símbolos conectivos lógicos
p: Chile está en Asia
q: 2 por 2 es igual a 4
p∧q
p ∧ ( ¬q )
Chile está en Asia y 2 por 2 es igual a 4
(¬p ) ∧ (¬q )
Chile no está en Asia y 2 por 2 no es igual a 4
p∨q
Chile está en Asia o 2 por 2 es igual a 4
p ∨ ( ¬q )
Chile está en Asia o 2 por 2 es no igual a 4
( ¬p ) ∨ q
Chile no está en Asia o 2 por 2 es igual a 4
Desarrollado por
Ricardo Soto De Giorgis
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería Informática
3.3 – Tablas de verdad
Una fórmula bien formada es una fórmula sintácticamente correcta
a) Toda variable proposicional es una fórmula bien formada (fbf)
(¬A) es fbf
( A ∧ B), ( A ∨ B), ( A ⇒ B), ( A ⇔ B)
c) Si A y B son (fbf) también lo son
Cualquier fbf se obtiene aplicando un nº finito de veces los puntos a,b,c.
Las tablas de verdad definen el significado de una sentencia
Debido a que el lenguaje es composicional el significado de una sentencia se
puede obtener a partir del significado de sus partes.
TAUTOLOGIA: la fórmula es verdadera para todos lo valores posibles de sus
variables proposicionales
CONTRADICCION: la fórmula es falsa para todos lo valores posibles de sus
variables proposicionales
CONTINGENCIA: la fórmula es verdadera o falsa dependiendo de los valores
de verdad de sus variables proposicionales.
p
V
V
F
F
Desarrollado por
Ricardo Soto De Giorgis
Chile está en Asia y 2 por 2 no es igual a 4
Capítulo 3 – Cálculo proposicional
3.2.1 – Fórmulas bien formadas
b) Si A es fbf entonces
Escuela de Ingeniería Informática
Capítulo 3 – Cálculo proposicional
3.1 - Introducción
Desarrollado por
Ricardo Soto De Giorgis
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería Informática
Capítulo 3 – Cálculo proposicional
Desarrollado por
Ricardo Soto De Giorgis
q
V
F
V
F
p∧q
p∨q
V
F
F
F
V
V
V
F
p⇒q p⇔q
V
F
V
V
¬p
¬q
F
F
V
V
F
V
F
V
V
F
F
V
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
PONTIFICIA
UNIVERSIDAD CATOLICA DE VALPARAISO
Escuela de Ingeniería Informática
Capítulo 3 – Cálculo proposicional
3.4 – Leyes del Cálculo proposicional
3.4 – Leyes del Cálculo proposicional
Doble negación
Leyes conmutativas
Leyes de DeMorgan
Leyes asociativas
Contrapositiva
Implicación
Leyes distributivas
Leyes de idempotencia
Equivalencia
Leyes de identidad
Ley de exportación
Reducción al absurdo
Desarrollado por
Ricardo Soto De Giorgis
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
Desarrollado por
Ricardo Soto De Giorgis
Escuela de Ingeniería
Informática
INF 152 – Programación en Lógica
1