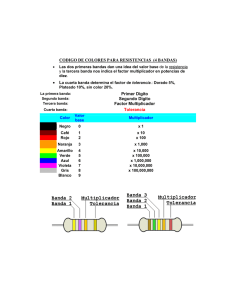
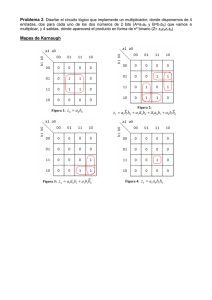
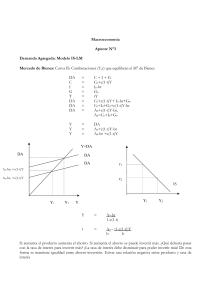
Ejercicio 1A

MACROECONOMÍA
PRIMER CURSO DE GADE
CURSO 2009-2010
CARLOS PATEIRO RODRÍGUEZ
Catedrático de E.U.E.E
LAURA VARELA CANDAMIO
Profesora de la asignatura
EJERCICIO Nº 1-A
Suponga el siguiente modelo de economía cerrada con sector público, donde
C= 50 + 0,625Yd es la función de consumo (Yd es la renta disponible).
Sean 100 y 200, respectivamente, la inversión y el gasto público, y 0,2 el tipo
impositivo
Se pide:
a. Calcular la renta de equilibrio
b. Calcular el valor del multiplicador del gasto público
c. Calcular el incremento que experimentará la renta de equilibrio si el gasto
público aumenta en 50 unidades monetarias
d. Encuentre una expresión para la función de ahorro
e. Compruebe que C+I+G=Y
f. Compruebe que S+T=I+G
g. Haga una representación gráfica del equilibrio
1
SOLUCIONES
C= 50 + 0,625Yd
a) En una economía con sector público: Y = C + I + G
C= C0 + cYd
Sabiendo que Yd =Y-tY
C= C0 + cYd = C0 + c(Y-tY) = 50 + 0,625(Y – 0,2Y)
= 50 + 0,625Y – 0,125Y
C=50 + 0,5Y
I = I0 = 100
G = G0 = 200
Y0
Y
Y-0,5Y
0,5Y
=C+I+G
= 50 + 0,5Y + 100 + 200
= 50 + 100 + 200
= 200
Y0 = 700
b) El multiplicador (teniendo en cuenta la existencia de impuestos):
c) La relación que existe entre la variación de la renta y la del
componente autónomo del gasto público
se calcula gracias al
multiplicador (teniendo en cuenta la existencia de impuestos):
=
=
= 2 x 50 = 100
>
Nótese que la variación en el gasto público,G0 , provoca una
variación en la renta del mismo sentido y de mayor proporción porque el
multiplicador es mayor que uno
2
En consecuencia, la nueva renta de equilibrio es:
= 700 + 100 = 800
Y1 = 800
d) La función de ahorro:
d.1) Si la calculamos en función de la renta disponible (Yd):
Podemos hallar la función de ahorro S= S0 + sYd a partir de la función de
consumo, calculada en el primer apartado:
S= -C0 +(1- c)Yd
= -50 + (1-0,625) Yd
S = -50 + 0,375 Yd
Notése que c’ + s’ = 1 cuando consumo y ahorro se expresan en
función de la renta disponible (0,625 + 0,375) = 1
d.2) Si la calculamos en función de la renta (Y):
Sabiendo que Yd =Y-tY
S= -C0 +(1- c)Yd
= -C0 +(1- c)(Y-tY)
= -C0 +(1- c)Y-(1-c)tY
= -C0 +(1- c)Y(1-t)
= -C0 +(1- c)(1-t)Y
= -50 +(1- 0,625)(1-0,2)Y
S=-50 + 0,3Y
Notése que c’ + s’+ t’ = 1 cuando consumo y ahorro se expresan en
función de la renta (0,5 + 0,3+0,2) = 1
e) Comprueba que C+I+G=Y0
Como Y0=700
C=50 + 0,5Y = 50 + 0,5x700 = 400
I = I0 = 100
G = G0 = 200
3
C+I+G=Y0
400 +100 + 200= 700
f) Comprueba que S+T = I + G
S=-50 + 0,3Y = -50 + 0,3x700 = 210-50=160
T=tY
= 0,2x700
=140
I = I0 = 100
G = G0 = 200
S+T = I + G
160 + 140 = 100 +200
NOTA: Advertir que tanto la función de consumo como la del ahorro se
pueden expresar en función de la renta disponible (Yd) o en función de la
renta (Y). En este caso, como lo que perseguimos es la renta de equilibrio,
siempre utilizaremos dichas funciones en términos de la renta (Y).
g) Represente gráficamente el equilibrio
DA
45º
DA
S, T
YE
= 700
I, G
Y
S+T
I+G
300
YE
=700
Y
(S+T) = S0 + sYd +tY = S0 + s(Y-tY) +tY Es creciente con la renta (depende de Y)
4
(I+G) NO depende de la renta, son componentes autónomos.
5