La Estadística se puede dividir en tres ramas: Estadística

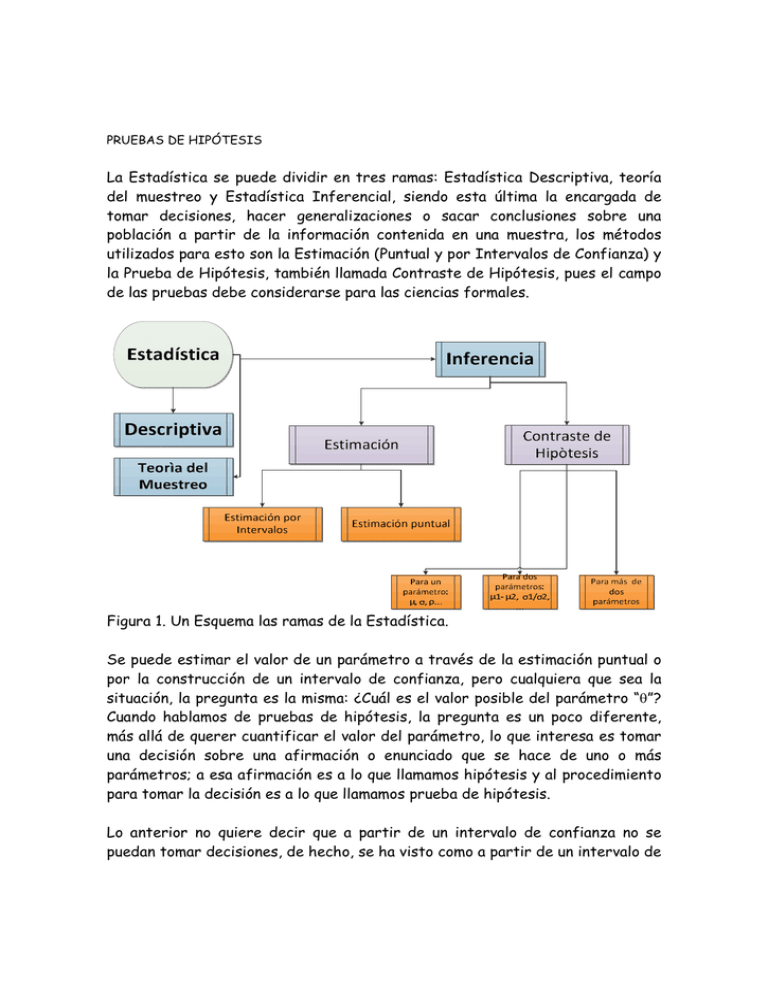
PRUEBAS DE HIPÓTESIS
La Estadística se puede dividir en tres ramas: Estadística Descriptiva, teoría
del muestreo y Estadística Inferencial, siendo esta última la encargada de
tomar decisiones, hacer generalizaciones o sacar conclusiones sobre una
población a partir de la información contenida en una muestra, los métodos
utilizados para esto son la Estimación (Puntual y por Intervalos de Confianza) y
la Prueba de Hipótesis, también llamada Contraste de Hipótesis, pues el campo
de las pruebas debe considerarse para las ciencias formales.
Figura 1. Un Esquema las ramas de la Estadística.
Se puede estimar el valor de un parámetro a través de la estimación puntual o
por la construcción de un intervalo de confianza, pero cualquiera que sea la
situación, la pregunta es la misma: ¿Cuál es el valor posible del parámetro “θ”?
Cuando hablamos de pruebas de hipótesis, la pregunta es un poco diferente,
más allá de querer cuantificar el valor del parámetro, lo que interesa es tomar
una decisión sobre una afirmación o enunciado que se hace de uno o más
parámetros; a esa afirmación es a lo que llamamos hipótesis y al procedimiento
para tomar la decisión es a lo que llamamos prueba de hipótesis.
Lo anterior no quiere decir que a partir de un intervalo de confianza no se
puedan tomar decisiones, de hecho, se ha visto como a partir de un intervalo de
confianza se pueden establecer o plantear afirmaciones sobre los parámetros
de una población, lo que ocurre es que la prueba de hipótesis es el método
estadístico más utilizado con ese fin.
La respuesta a cualquier pregunta de investigación puede clasificarse en una de
dos regiones posibles: p.e., “la producción, R, es mayor de tres toneladas”
¿R?
R>3
R≤3
Hipótesis Estadística: Están constituidas por un par de afirmaciones
complementarias y mutuamente excluyentes acerca de los parámetros de una o
más poblaciones y que todavía está por comprobar.
Prueba o Contraste de Hipótesis: Es el procedimiento que te va a permitir
tomar una decisión o dictaminar a cerca del valor de verdad de un juego de
hipótesis: no rechazar o rechazar la hipótesis planteada, usando la información
muestral como guía.
El seguimiento del método no implica o garantiza la certeza del dictamen, para
ello sería necesario examinar toda la población, pero si mantiene una de las
tasas de error bajo control.
PASOS GENERALES AL HACER UNA PRUEBA DE HIPÓTESIS.
1. PLANTEAMIENTO DE HIPÓTESIS.
Para realizar un contrate de hipótesis el primer paso es, con base en el
conocimiento previo que se tenga del fenómeno y de acuerdo a la forma en la
que se obtuvo la muestra, plantear las hipótesis que serán evaluadas. Un
modelo probabilístico para las variables que integran la muestra siempre hace
parte de los supuestos. Supongamos que se está trabajando en un cultivo de
fríjol y se tiene una hipótesis según la cual, la altura promedio de una planta de
fríjol a los 30 días es 25 cm; entonces, para cubrir las dos posibilidades (1: que
la altura promedio efectivamente sea 25 cm, 2: que la altura promedio no sea
25 cm) se plantean dos hipótesis, la primera -llamarla hipótesis nula, se
2
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
representar por el símbolo "Ho", esta hipótesis SIEMPRE se plantear en
términos de una igualdad (la nulidad de los efectos: no pasa nada), o sea
utilizando el símbolo "=", en este caso tu hipótesis nula sería:
Ho: µ =25 cm
La definición de hipótesis estadística especifica que la afirmación se hace
acerca de PARÁMETROS, por eso al plantear las hipótesis deben aparecer
parámetros como: µ, σ2 o P; y nunca estadísticos como: X , S2 o P̂
La segunda hipótesis -hipótesis alterna, se representa por el símbolo "Ha", y
puede presentar tres opciones según sea la pregunta del investigador (se
plantea sólo una):
a. Las plantas podrían tener un crecimiento mayor y medir más de 25 cm, la
hipótesis alterna quedaría:
Ha:µ > 25 cm
b. Las plantas podrían ser unas raquíticas y medir menos de 25 cm, con lo que la
hipótesis alterna quedaría:
Ha: µ < 25 cm
c. En la tercera opción no estás seguro si la altura a los 30 días podría ser
mayor o menor de 25 cm, podría ser cualquiera de los dos, entonces para cubrir
esas dos posibilidades se plantea la hipótesis alterna en términos de "
diferente de ", con el símbolo "≠" y quedaría:
Ha: µ ≠ 25 cm
A las opciones a y b, las vas a llamar hipótesis unilaterales, unidireccionales o
de una sola cola y a la opción c: hipótesis bilateral , bidireccional o de dos colas;
la opción de trabajar con una hipótesis alterna unilateral o bilateral depende
del investigador, las hipótesis unilaterales generalmente se plantean cuando ya
hay un conocimiento previo de la situación, que permite suponer hacia qué lado
podría estar la diferencia y las bilaterales se plantean cuando se desconoce
hacia cuál de los dos lados podría estar la diferencia.
3
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
En los contrastes de hipótesis lo que se hace es probar la hipótesis nula y
tomar una decisión: No rechazarla o rechazarla; se debe tener presente que
“La estadística no prueba nada”, nunca se va a tener la absoluta certeza sobre
la veracidad o falsedad de una hipótesis, a menos que se evalúe toda la
población, lo cual no es práctico, entonces lo que se hace es tomar una muestra
y evaluar si los datos de la muestra apoyan o no la hipótesis nula; de tal manera
que si no rechazamos Ho, no quiere decir que Ho sea cierta, en realidad lo que
estás concluyendo es que la muestra no aporta evidencias suficientes para
rechazar la hipótesis nula; cuando rechazamos Ho, estamos afirmando que
tenemos evidencias en contra de Ho, que es más factible que la Ha sea la
verdadera, pero aún así, podrías estar equivocado.
2. DEFINIR DISTRIBUCIÓN DE PROBABILIDADES A USAR.
Después de haber planteado el juego de hipótesis, el paso siguiente es definir
la distribución de probabilidades a utilizar, lo cual no siempre es simple:
Si la hipótesis es sobre medias y los datos provienen de una distribución
normal, sólo tenemos dos opciones: distribución "T" de Student o distribución
"Z", la decisión depende de si se conoce o no la varianza poblacional (σ2), si es
conocida vas a utilizar la distribución "Z" y si es desconocida, vas a utilizar la
distribución "T”.
Si la hipótesis es sobre varianzas y los datos provienen de una distribución
normal, también hay dos opciones:
a. La hipótesis es para una sola varianza, es decir, la hipótesis nula sería
del tipo:
Ho: σ2 = 15 cm2
En este caso utilizarías la distribución X2 (Ji-cuadrado) ver Walpole y Myers.
b. La hipótesis compara dos varianzas : donde la hipótesis nula sería del
tipo:
Ho: σ12 =σ22
Y aquí la distribución que vas a usar es la "F".
Si la hipótesis es sobre proporciones también hay dos opciones:
a. La hipótesis es para una sola proporción, es decir, la hipótesis nula sería
del tipo:
4
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
Ho: P = 0.6
En este caso vas a utilizar la distribución Binomial
b. La hipótesis es para dos proporciones, es decir, la hipótesis nula sería
del tipo:
Ho: P1 = P2
Aquí la distribución a usar es la "Z”. Ya se ha mencionado que la aproximación
de la distribución Binomial a la distribución "Z" no siempre es adecuada, sin
embargo en este tipo de hipótesis es la única opción, la condición es tener un
tamaño de muestra grande, o que tus datos cumplan con alguna de las
siguientes condiciones: p*n ≥ 5 y p*q ≥ 5.
3. DEFINIR NIVEL DE SIGNIFICANCIA.
Ahora que ya tenemos definidas las hipótesis y la distribución a utilizar, el
paso siguiente es definir el "nivel de significación" o “nivel de la prueba”, (α,
alpha) que se usará; este concepto está muy relacionado con el mencionado
“nivel de confianza” (1- α) al trabajar con intervalos de confianza. Para
entender este concepto en el contexto véase la siguiente tabla:
Decisión frente a Ho
(tomada a partir de la
muestra)
Rechazo
No rechazo
Realidad de la hipótesis nula (Desconocida)
Verdadera
Falsa
Error tipo I
Decisión correcta
Decisión correcta
Error Tipo II
Ante cualquier hipótesis se pueden tomar dos decisiones: o la aceptas o la
rechazas. Y para cualquier decisión que se tome hay dos opciones: acierto o
error, estas opciones son el interior de la tabla.
Desafortunadamente, al tomar una decisión respecto a una hipótesis siempre
existe la posibilidad de cometer un error, no podemos estar seguros de que
efectivamente la hipótesis sea verdadera y simplemente lo que decimos es que
la muestra no aporta evidencias suficientes para rechazar la hipótesis nula.
Cuando se rechaza una hipótesis y ésta, en realidad era verdadera, se está
cometiendo un error de tipo I (es el error menos afortunado, como cuando se
condena un inocente) y a la máxima probabilidad de cometer este error se le
llama: α (alfa), o "nivel de significancia":
5
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
Nivel de Significancia (α): Es la máxima probabilidad de cometer un error de
tipo I, o sea la máxima probabilidad de rechazar una Hipótesis nula que era
verdadera.
El nivel de significancia (alfa) siempre es definido de antemano por el
investigador, el porqué de esto obedece a que, el objetivo real del investigador
siempre es rechazar la hipótesis nula y por lo tanto aprobar la hipótesis
alterna, por eso, a esta última a veces se le llama también hipótesis del
investigador, entonces resulta conveniente conocer de entrada cuál es la
probabilidad de equivocarse al rechazar la hipótesis nula.
Cuando se define un α: 0.05 se está diciendo que se está dispuesto a cometer
el error tipo I como máximo el 5% de las veces; o sea que de cada 100 veces
que a partir de los datos se concluya a favor de la hipótesis alterna, se tolera
equivocarse como máximo, en cinco de esas 100 veces. Los niveles de
significación más utilizados en las ciencias biológicas son 0.05 y 0.01.
Ahora, si no se rechaza una hipótesis nula que en realidad era falsa, se está
cometiendo un error de tipo II (es menos pernicioso pues otro investigador,
posteriormente la puede desenmascarar) y a la probabilidad de cometer este
error se le llama: β (Beta).
β (Beta): Es la probabilidad de cometer un error de tipo II, es decir, es la
probabilidad de no rechazar una hipótesis nula que era falsa.
Siempre es deseable que alfa y beta sean lo más pequeños posibles, pero estos
están relacionados de tal manera que si el uno disminuye, el otro aumenta. La
única manera de que uno disminuya y el otro permanezca constante o disminuya
también, es aumentar el tamaño de la muestra para trabajar con distribuciones
2
2
más leptocúrticas (σ X = σ X / n) .
6
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
Figura 2. Arriba la distribución bajo la hipótesis nula, abajo la distribución bajo la
hipótesis alterna
Figura 3. Regiones de rechazo para alpha = 0,05 (izquierda) y alpha = 0,01 (derecha),
cuando n = 1, s = 1 y H0: µ ≤ µ0, Ha: µ > µ0 Nótese como con el aumento del nivel, la
región azul –la potencia- disminuye.
Otro elemento de los contrates de hipótesis es la "Potencia" definida como (1 β): la probabilidad de rechazar una hipótesis nula que es falsa, ésta es una
probabilidad que se desea que sea lo más grande posible.
Potencia (1 - β): Es la probabilidad de rechazar una hipótesis nula falsa.
7
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
Decisión frente a Ho
(tomada a partir de la
muestra)
Rechazo
No rechazo
Realidad de la hipótesis nula (Desconocida)
Verdadera
Falsa
Error tipo I
P(Error I) máxima = alpha
Decisión correcta
P(correcta) = 1- alpha
Decisión correcta
P(correcta) = Beta
Error Tipo II
P(Error II) = potencia
4. PRUEBA DE LA HIPÓTESIS
En esta etapa, de acuerdo al parámetro evaluado y a la distribución de probabilidades escogida
en el paso 2, se define una regla para probar la hipótesis y se decide si se rechaza.
Hipótesis sobre una media cuando se conoce la varianza poblacional
(σ
σ2).
Ahora vamos a hacer la prueba de hipótesis para el siguiente ejemplo: La empresa vende
champiñones empacados en bandejas al vacío, en cuya etiqueta se lee: "Contenido 450 gramos",
el servicio nacional del consumidor recibió varios reclamos del público en donde se señalaba que
el contenido de las bandejas es menor al indicado en la etiqueta; se tomaron 45 bandejas como
muestra, obteniendo un peso promedio de 445 gramos, si asumimos que el peso de las bandejas
sigue una distribución normal y la varianza poblacional es de 25 g2; con un nivel de significancia
de 0.01, será que es válida la denuncia contra la empresa?
El primer paso es definir las hipótesis, como la hipótesis nula debe hacerse en términos de
igualdad, entonces se plantea que el peso promedio de las bandejas de champiñones es el que
aparece en la etiqueta: 450 g Ho: µ =450 g
De acuerdo al enunciado, los consumidores creen que el peso de las bandejas es menor, por lo
tanto se espera que el peso promedio de las bandejas sea menor que el que aparece en la
etiqueta, con lo que la hipótesis alterna quedaría:
Ha: µ < 450 g
El segundo paso es definir la distribución que se va a usar, como se trata de promedios y se
conoce la varianza poblacional, entonces se utiliza la distribución "Z". El nivel de significancia
ya está dado: alfa = 0.01.
Ahora hay que establecer una regla de decisión, que en términos de la variable original es:
escoger un peso máximo por debajo del cual vas a considerar que efectivamente el peso
promedio de las bandejas es inferior a 450 g, ¿ pero cuál es ese punto de corte? 449, 448,
440???
En realidad lo que se hace es escoger un punto de corte pero no en términos de la variable
original si no en términos de un valor de la distribución que se va a usar, en este caso, un valor
de "Z", a este "Z" lo vas a llamar "Z Crítico" o "Z teórico" = "Zt", que debe cumplir:
8
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
P(Z ≤ Zt) = α
Lo que equivaldría a buscar un valor de "Z" tal que la probabilidad de encontrar valores
menores o iguales a él, sea de 0.01, si vas a la tabla vas a encontrar que Zt = -2.3263
(interpolando)
En este caso el ≤ está dado por la hipótesis alterna, que es unilateral a la izquierda y alfa es el
nivel de significancia (0.01) ya mencionado ; como el punto de corte lo definimos en términos de
una variable Z, entonces la media muestral obtenida debemos llevarla también a su equivalente
en la distribución Z, a este equivalente es a lo que se le llama el estadístico de prueba: un valor
de "Z" correspondiente a los datos observados y que vas a llamar "Z calculado" = "Zc" y que se
obtiene a partir de la fórmula:
Zc:
(X − µ )
0
σ



n

X y σ serían el promedio aritmético de los datos observados y la desviación estándar
poblacional, que en este caso serían 445 g y 5 g respectivamente; µ0 es la media poblacional
Donde
según la hipótesis nula = 450 g y "n" es el número de datos = 45.
Figura 4. Distribución de la población bajo hipótesis nula y bajo hipótesis alterna. El área rosa
es el nivel, alpha, el área azul, la probabilidad Beta
En la figura 4 se puede ver dos distribuciones, la de la derecha es bajo la hipótesis nula donde
µ=450 g. y la de la izquierda es la distribución bajo hipótesis alterna, que dice que µ < 450 g.,
Zt es el punto de corte tal que P(Z ≤ Zt) = α, es decir que el área del gráfico que esta rayada
es α, recordemos su definición: es la máxima probabilidad de rechazar una hipótesis nula
verdadera, entonces, si nuestro estadístico de prueba Zc (o sea el equivalente de la media
observada a partir de la muestra) es un valor tal que cae en el área rosada, podríamos pensar
que nuestros datos pertenecen realmente a la distribución de la izquierda con µ < 450 g. y
rechazar Ho, pero debemos tener presente que todavía existe la posibilidad de que nuestros
9
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
datos si pertenezcan a la distribución de la derecha y Ho sea verdadera, esa posibilidad es el
área rosada, o sea alfa.
El área azul es Beta, recordemos su definición: es la probabilidad de no rechazar una Ho falsa,
entonces; si nuestro estadístico de prueba Zc (o sea el equivalente de la media observada a
partir de la muestra) es un valor tal que cae en el área azul, podríamos pensar que nuestros
datos pertenecen realmente a la distribución de la derecha con µ = 450 g. y no rechazar Ho,
pero todavía existe la posibilidad de que nuestros datos si pertenezcan a la distribución de la
izquierda y Ho sea falsa, esa posibilidad es el área azul, o sea beta.
El área a la izquierda de Zt se llama región de rechazo ( en este caso específico es el área a la
izquierda porque la hipótesis alterna era unilateral a la izquierda) y el área a la derecha de Zt
se llama región de no rechazo, entonces vamos a decir que se rechaza Ho si se cumple que: Zc ≤
Zt
Si se estandariza 445 (el promedio de la muestra), se obtiene que: Zc = -6.708 ≤ - 2.3267 por
lo tanto, la conclusión es que hay evidencia suficiente para rechazar Ho, debemos inclinarnos a
creer que la queja de los consumidores es válida, pero teniendo claro que existe la posibilidad
de que estemos equivocados y esa probabilidad es α = 0.01
Miremos ahora qué es lo que hay realmente detrás de esas llamadas regiones de rechazo y de
no rechazo; supongamos que efectivamente la población de pesos de bandejas de champiñones
tiene un peso medio de 450 g con una desviación estándar poblacional de 5 g, bajo ese
supuesto calculemos cuál es la probabilidad de encontrar un peso medio menor o igual a 445 g,
es decir P( X ≤ 445) que al estandarizar se convierte en P(Z ≤ -6.708) y que es un valor del
cuál lo único que podemos decir es que es inferior a 0.0002.
Si la hipótesis nula fuera cierta, es decir, el peso medio de las bandejas realmente es 450 g,
entonces tendríamos una probabilidad muy pequeña (por no decir despreciable) de encontrar
unos resultados como los que obtuvimos, es decir, que en una muestra de 45 bandejas se
obtenga una media de 445 g, lo cual nos lleva a pensar que tal vez la media no es en realidad
450 g y si nos dejamos llevar por esta impresión y tomamos la decisión de rechazar Ho y somos
tan de malas que Ho era verdadera, entonces ese valor que es inferior a 0.0002, sería
exactamente la probabilidad de estar cometiendo el error tipo I y a esta probabilidad la vamos
a llamar “valor P” de su nombre en inglés: P-value. En el ejemplo P-value = P(Z ≤ -6.708) =
Valor P, “alpha_gorro” o P-value: Es la probabilidad de obtener valores iguales o más extremos
que el estadístico de prueba calculado para los datos, en otras palabras: es la probabilidad de
que bajo la hipótesis nula, se presenten valores iguales o más extremos que el hallado en la
muestra.
En este se debe recordar que definimos el nivel de significancia (α) como la máxima
probabilidad de cometer un error tipo I, es decir, ese margen de error que se está dispuesto a
tolerar al rechazar Ho, ésta probabilidad es un valor definido a priori por el investigador,
10
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
mientras que el valor P es una probabilidad a posteriori obtenida a partir de los datos de la
muestra.
Al trabajar con el computador, éste calcula el valor P, y entonces se toma la decisión de
rechazar o no la hipótesis nula: la regla de decisión es la siguiente, vas a rechazar hipótesis
nula siempre que P-value ≤ α, porque si P-value es menor que α, quiere decir que nuestro
estadístico de prueba cayó en zona de rechazo.
Si la Ha hubiera sido unilateral a la derecha, es decir, si se creyera que el peso medio de las
bandejas es superior a 450 g. (Ha: µ > 450 g.) la regla sería rechazar Ho si: Zc ≥ Zt donde Zc
se obtiene con la misma fórmula, pero Zt ahora debe cumplir que P(Z ≥ Zt)=α, sólo para
practicar, si este hubiera sido nuestro caso Zt= 2.3267, recuerde que por la simetría de la
distribución, sólo es cuestión de cambiarle el signo al Zt hallado anteriormente, en este caso el
área de rechazo sería el área a la derecha de Zt y la región de no rechazo: el área a su
izquierda.
Si la Ha hubiera sido bilateral, la regla sería rechazar Ho si se cumple cualquiera de las dos
condiciones siguientes:
Zc ≤ -Zt
ó
Zc ≥ Zt
Que es equivalente a la expresión: | Zc ≥ Zt |, (en valor absoluto) con Zt tal que P(Z ≥ Zt)=
α/2, como la hipótesis es bilateral, se debe dividir el alfa entre dos y la región de no rechazo
estará comprendida entre -Zt y Zt, las dos zonas de rechazo estarían: a la derecha de Zt y a
la izquierda de –Zt.
Ejercicio.
En la finca “El mango” trabajan con la variedad de mango “pecoso” y se tiene una producción
promedio de 8 Ton/ha, en la finca de al lado hace seis meses empezaron a trabajar con la
variedad “jugoso” y están muy contentos con los resultados. Se decide evaluar la variedad
“jugoso” en 10 parcelas (c/u de una hectárea) y se encuentra una producción promedio de 8.15
Ton/ha, si se asume que la producción de mangos sigue una distribución normal con σ2 = 4 Ton2
/ha, se utiliza un nivel de significancia del 5%, tome una decisión sobre el futuro de la finca,
calcule el valor P del resultado obtenido en la muestra y el valor de alfa con el cuál cambiarías
la decisión tomada como resultado de la prueba de hipótesis.
PREGUNTA: ¿Cómo se puede llegar a la misma conclusión de la prueba de hipótesis con un
intervalo de confianza?
11
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín
Considere el problema de contrastar
H0: µ ≤ 10
Ha: µ > 10
Con n = 64, σ = 2 (conocida), y alpha = 0,025
La región de rechazo de la hipótesis nula está constituida por los promedios tales que
x − 10
2
≥ 1,96 o x ≥ 10 + 1,96*
= 10, 49
2
64
64
Si x = 10,6 , entonces Zc = 2,4 y como Zt = 1,96 se tienen elementos para rechazar la
H0, con un nivel de significancia de 0,025.
El valor P de la prueba (P-value) será igual a P(Z > 2,4).
Suponga que queremos calcular la potencia de la prueba de este contraste, bajo la
hipótesis alterna de que: µ1 = 11. Como nuestra prueba rechaza H0 cuando
,
la potencia en µ1 = 11 es la probabilidad
P[ x ≥ 10, 49 cuando µ = 11] = P[ Z ≥
x − 11
10, 49 − 11
] = P[ Z ≥
]=P[ Z ≥ −2,04 ] = 0,9793
0, 25
0, 25
Conclusión: Cuando se plantea H0: µ ≤ 10 vs Ha: µ > 10; Si el verdadero valor de la media
poblacional fuera 11, la
σ =
2, se trabaja con una muestra de tamaño 64 y se fija un nivel de
significancia del 2,5%, entonces, en el 97,93% de los casos se rechaza la hipótesis nula.
Ejercicio:
• Calcule la potencia de esta prueba si el verdadero valor de la media es 10,5
• Calcule la potencia de esta prueba si el verdadero valor de la media es 10,8
• Calcule la potencia de esta prueba si el verdadero valor de la media es 11,5
• Recalcule estas probabilidades para tamaños de muestra n = 36 y n = 100.
12
Jairo Alberto Rueda Restrepo [email protected] Sede Medellín