1 5 CURVAS INTENSIDAD, DURACIÓN Y FRECUENCIA (IDF). Las
Anuncio

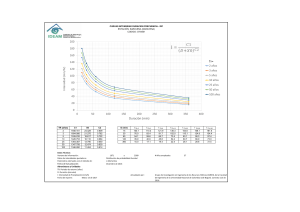
5 CURVAS INTENSIDAD, DURACIÓN Y FRECUENCIA (IDF). Las curvas IDF, son una técnica que permite obtener información de las lluvias esperadas en una región, teniendo en cuenta tres de sus variables más importantes: su intensidad, duración y frecuencia o tiempo de retorno. Esta técnica aunque antigua en su concepto, es muy vigente y de amplio uso en ingeniería, sobre todo para el diseño de obras hidráulicas y de gestión de recursos hídricos. Las curvas IDF, se presentan generalmente como un grupo de curvas, cada una de las cuales representa un período de retorno dado. En el eje X se tiene la duración del evento (lluvia) y en el eje Y, la Intensidad del mismo. Se debe hacer claridad que para poder utilizar esta técnica, se debe contar con una estación meteorológica cercana, la cual debe contar con mediciones hidrológicas de un periodo largo, ojala 30 años, necesariamente obtenidas con pluviógrafo, dado que lo que se analiza es el pluviograma. En términos generales para la construcción de una curva IDF, deben seguirse los siguientes pasos. 1. Determinar el periodo de registro con que se cuenta ([años]), entre mas largo mejor. 2. Para cada año seleccionar las 5 mayores lluvias (magnitud [mm]). 3. Para cada año, del pluviograma de las 5 lluvias seleccionadas, determinar la intensidad [mm/min], para los siguientes periodos de tiempo: 5, 10, 20, 30, 60, 120 y 360 minutos. 4. Para cada año y tiempo de observación, escoger la mayor intensidad de las mediciones de las 5 lluvias. 5. Convertir las intensidades encontradas en el paso anterior de [mm/min] a [mm/hora]. 6. Construir una Tabla donde se coloque en la primera columna los años de medición, seguido de columnas donde se colocan los valores de Intensidad, conservando una columna para cada uno de los periodos de tiempo seleccionados. 7. Calcular la probabilidad de estas intensidades usando la distribución de valores extremos o de Gumbel. 8. Para cada uno de los periodos de tiempo seleccionados y la probabilidad obtenida, obtener la ecuación de la recta que representa a esta nube de puntos. 9. Con las ecuaciones de las rectas, para cada duración, obtener los valores de intensidad máxima para 2, 5, 10, 20, 50 , 100 y 200 años. 10. Con estos datos, construir la curva IDF. 1 Ejemplo 8. Calcular la gráfica IDF, para la serie de datos que hemos venido manejando en los ejemplos anteriores. Para esto aplicaremos la metodología recomendada. 1. Determinar el periodo de registro con que se cuenta ([años]), entre mas largo mejor. En este caso contamos con 25 años de mediciones, por lo que la longitud de la serie es aceptable. 2. Para cada año seleccionar las 5 mayores lluvias (magnitud [mm]). En este caso se debe seleccionar de entre todos los pluviogramas las cinco lluvias que presenten una mayor magnitud. 3. Para cada año, del pluviograma de las 5 lluvias seleccionadas, determinar la intensidad [mm/min], para los siguientes periodos de tiempo: 5, 10, 20, 30, 60, 120 y 360 minutos. En este caso por facilidad de lectura, lo mejor es construir la curva de masa de cada lluvia, aunque la práctica permite tomar en forma muy simple estos valores directamente del pluviograma. Vamos a analizar un evento para mostrar la forma de hacerlo, a partir de la curva de masa respectiva. Figura 1. Curva de masa para determinar la magnitud en cada periodo de tiempo. 250 Magnitud [mm] 200 150 100 50 0 0 50 100 150 200 250 Tiempo acumulado [min] 300 350 400 2 Se observa que la Gráfica anterior presenta una cuadrícula densa, separada cada 5 minutos en el eje X y cada 5 mm en el eje Y. A partir de este gráfico lo que debe hacerse es determinar la magnitud para cada uno de los periodos de tiempo determinados, por ejemplo para el de 5 minutos, se evalúa a partir de cero, donde la magnitud es cero, después en cinco, luego en 10 y así sucesivamente. En la siguiente Tabla se muestran por ejemplo los datos de magnitud para un periodo de tiempo de 30 minutos, basados en la Figura 1. Tabla 1. Valores de magnitud e intensidad para un periodo de tiempo de 30 minutos. TIEMPO ACUMULADO (min) 0 30 60 90 120 150 180 210 240 270 300 330 360 MAGNITUD (mm) INTENSIDAD (mm/min) 0 20 30 35 45 51 60 68 81 98 121 150 179 0,00 0,67 0,50 0,39 0,38 0,34 0,33 0,32 0,34 0,36 0,40 0,45 0,50 4. Para cada año y tiempo de observación, escoger la mayor intensidad de las mediciones de las 5 lluvias. De acuerdo con la Tabla 1, la mayor intensidad para esta lluvia es de 0.67mm/h. 5. Convertir las intensidades encontradas en el paso anterior de [mm/min] a [mm/hora]. Para convertir mm/min a mm/h, basta multiplicar la primera por 60. 6. Construir una Tabla donde se coloque en la primera columna los años de medición, seguido de columnas donde se colocan los valores de Intensidad, conservando una columna para cada uno de los periodos de tiempo seleccionados. 3 En la Tabla 2, se presentan los datos completos de una serie de datos de 25 años de longitud, con las cuales vamos a construir la curva IDF correspondiente. Tabla 2. Valores de intensidad máxima para varios periodos de tiempo. AÑO 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Media Des Est DURACIÓN (min) / INTENSIDAD (mm/h) 5 10 20 30 60 120 360 19,5 18,4 26,8 28,6 29,9 19,4 25,4 28,0 22,6 28,1 27,3 25,2 19,0 19,7 24,3 25,6 24,8 25,7 27,1 25,2 24,1 28,3 22,8 23,7 28,4 24,7 3,37 15,5 22,6 24,9 18,9 26,8 18,9 14,9 17,5 22,8 24,8 21,0 19,6 26,7 20,4 19,0 14,5 17,8 19,8 25,8 24,6 19,4 22,4 23,8 24,2 26,0 21,3 3,72 13,5 18,6 17,6 13,5 18,9 18,8 17,5 12,8 14,6 15,8 16,7 16,1 15,7 15,3 14,8 18,6 17,1 16,2 14,5 18,2 15,2 13,7 17,5 18,2 13,7 16,1 1,92 12,5 11,8 14,6 16,8 17,5 15,6 14,3 12,7 13,8 14,5 12,9 14,8 16,3 14,3 12,9 14,8 11,8 11,9 12,3 13,7 14,2 12,6 14,1 12,6 13,8 13,9 1,54 10,5 11,8 10,9 14,6 14,5 12,6 13,4 14,2 11,5 10,9 12,8 14,1 13,5 14,8 13,6 11,7 12,7 12,6 14,6 13,8 12,9 11,0 10,7 14,3 17,5 13,0 1,67 8,3 8,9 9,6 10,2 11,5 9,5 8,9 11,2 10,6 10,7 9,7 8,4 8,9 10,2 10,8 9,7 8,8 7,8 8,3 9,4 10,6 11,2 10,8 9,7 9,3 9,7 1,03 5,6 5,8 6,3 6,6 7,5 7,4 5,8 6,7 6,4 5,3 7,2 6,9 6,4 5,3 5,7 6,2 6,3 7,1 6,9 5,8 5,3 5,4 6,7 5,7 5,8 6,2 0,68 7. Calcular la probabilidad de estas intensidades usando la distribución de valores extremos o de Gumbel. Para asignar la probabilidad utilizamos la ecuación de Gringorten, con lo cual la Tabla 2 queda: 4 Tabla 3. Valores de intensidad y probabilidad para varios periodos de tiempo. AÑO 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 DURACIÓN (min) / INTENSIDAD (mm/h) 5 10 20 30 60 120 360 19,5 18,4 26,8 28,6 29,9 19,4 25,4 28,0 22,6 28,1 27,3 25,2 19,0 19,7 24,3 25,6 24,8 25,7 27,1 25,2 24,1 28,3 22,8 23,7 28,4 15,5 22,6 24,9 18,9 26,8 18,9 14,9 17,5 22,8 24,8 21,0 19,6 26,7 20,4 19,0 14,5 17,8 19,8 25,8 24,6 19,4 22,4 23,8 24,2 26,0 13,5 18,6 17,6 13,5 18,9 18,8 17,5 12,8 14,6 15,8 16,7 16,1 15,7 15,3 14,8 18,6 17,1 16,2 14,5 18,2 15,2 13,7 17,5 18,2 13,7 12,5 11,8 14,6 16,8 17,5 15,6 14,3 12,7 13,8 14,5 12,9 14,8 16,3 14,3 12,9 14,8 11,8 11,9 12,3 13,7 14,2 12,6 14,1 12,6 13,8 10,5 11,8 10,9 14,6 14,5 12,6 13,4 14,2 11,5 10,9 12,8 14,1 13,5 14,8 13,6 11,7 12,7 12,6 14,6 13,8 12,9 11,0 10,7 14,3 17,5 8,3 8,9 9,6 10,2 11,5 9,5 8,9 11,2 10,6 10,7 9,7 8,4 8,9 10,2 10,8 9,7 8,8 7,8 8,3 9,4 10,6 11,2 10,8 9,7 9,3 5,6 5,8 6,3 6,6 7,5 7,4 5,8 6,7 6,4 5,3 7,2 6,9 6,4 5,3 5,7 6,2 6,3 7,1 6,9 5,8 5,3 5,4 6,7 5,7 5,8 P(X<x) 0,022 0,062 0,102 0,142 0,182 0,221 0,261 0,301 0,341 0,381 0,420 0,460 0,500 0,540 0,580 0,619 0,659 0,699 0,739 0,779 0,818 0,858 0,898 0,938 0,978 8. Para cada uno de los periodos de tiempo seleccionados y la probabilidad obtenida, obtener la ecuación de la recta que representa a esta nube de puntos. Para obtener la ecuación de la recta para cada periodo de tiempo, usaremos el método analítico (presentado en el documento 3). 0.7797 * S X 0.5772 5 Las Ecuaciones de cada una de las rectas son: Y X Y5 2.629 X 23.198 Y10 2.898 X 19.631 Y20 1.494 X 15.262 Y30 1.203 X 13.190 Y60 1.301X 12.269 Y120 0.804 X 9.256 Y360 0.533 X 5.937 9. Con las ecuaciones de las rectas, para cada duración, obtener los valores de intensidad máxima para 2, 5, 10, 20, 50, 100 y 200 años. Para calcular los valores de intensidad máxima obtenemos primero el valor de la variable independiente en función del periodo de retorno. Por ejemplo para un periodo de 2 años tenemos: T 1 x ln( ln T 2 1 x ln( ln 5 1 x ln( ln 5 x 0.3665 Este valor se reemplaza en la Ecuación para cada uno de los periodos de tiempo. En la Tabla 3 se presentan los valores correspondientes. Tabla 3. Valores de intensidad máxima para varios periodos de retorno. DURACIÓN (min) 5 10 20 30 60 120 360 2 24,2 20,7 15,8 13,6 12,7 9,6 6,1 5 27,1 24,0 17,5 15,0 14,2 10,5 6,7 PERIODO DE RETORNO (años) 10 20 50 29,1 31,0 33,5 26,2 28,2 30,9 18,6 19,7 21,1 15,9 16,8 17,9 15,2 16,1 17,3 11,1 11,6 12,4 7,1 7,5 8,0 100 35,3 33,0 22,1 18,7 18,3 13,0 8,4 200 37,1 35,0 23,2 19,6 19,2 13,5 8,8 6 10. Con estos datos, construir la curva IDF. Basados en la Tabla 3, graficamos cada una de las duraciones en el Eje X, contra los valores de intensidad máxima en el Y, lo que nos da: Figura 1. Curva IDF, para el ejemplo. 35,5 Intensidad (mm/h) 30,5 2 años 25,5 5 años 10 años 20,5 20 años 50 años 100 años 15,5 200 años 10,5 5,5 0 50 100 150 200 Duración (min) 250 300 350 Con esta curva se obtienen fácilmente la intensidad máxima esperada para una duración y un periodo de retorno en particular. Por ejemplo se quiere saber cual es la intensidad máxima para una duración de 5 minutos y un periodo de retorno de 50 años. De acuerdo a la gráfica este valor corresponde a una lluvia con una intensidad máxima de 33.5 mm/h. 7