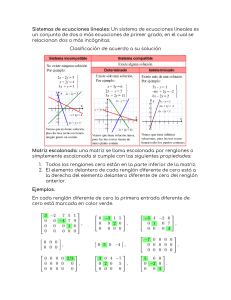
ECUACIÓN DE REDLICH-KISTER. (1) ln n g G RT n γ ∂ = = ∂ γ

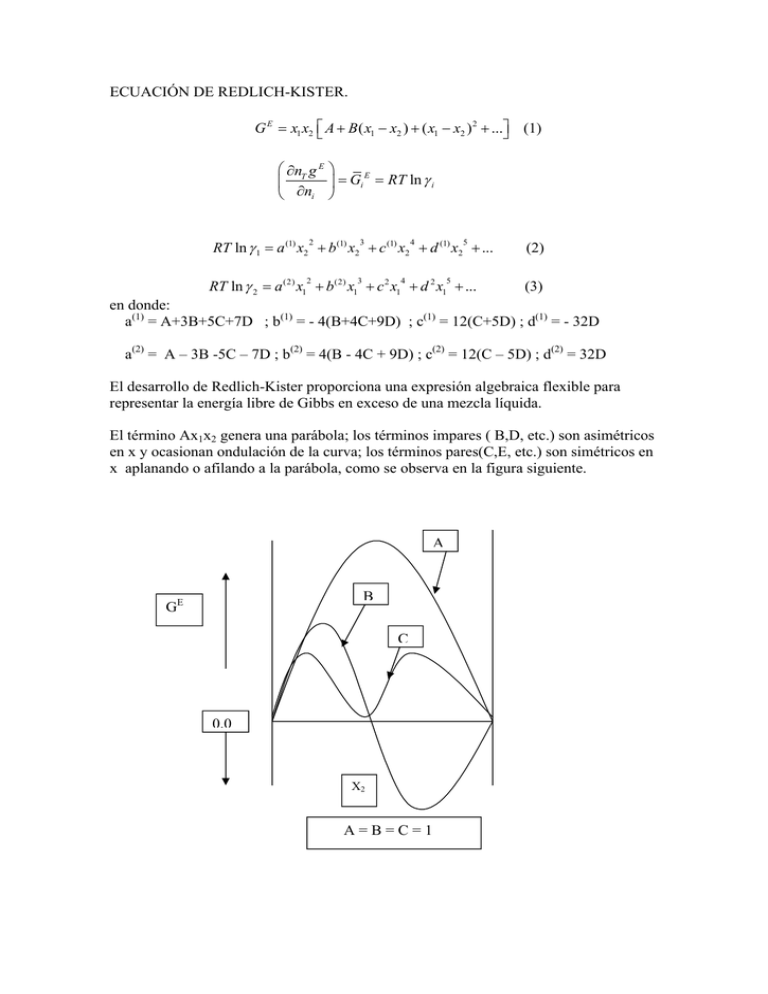
ECUACIÓN DE REDLICH-KISTER.
G E  x1 x2  A  B ( x1  x2 )  ( x1  x2 ) 2  ... (1)
 nT g E 
E

  Gi  RT ln  i
 ni 
RT ln  1  a (1) x2  b (1) x2  c (1) x2  d (1) x2  ...
(2)
RT ln  2  a (2) x1  b (2) x1  c 2 x1  d 2 x1  ...
(3)
2
2
3
3
4
5
4
5
en donde:
a(1) = A+3B+5C+7D ; b(1) = - 4(B+4C+9D) ; c(1) = 12(C+5D) ; d(1) = - 32D
a(2) = A – 3B -5C – 7D ; b(2) = 4(B - 4C + 9D) ; c(2) = 12(C – 5D) ; d(2) = 32D
El desarrollo de Redlich-Kister proporciona una expresión algebraica flexible para
representar la energía libre de Gibbs en exceso de una mezcla líquida.
El término Ax1x2 genera una parábola; los términos impares ( B,D, etc.) son asimétricos
en x y ocasionan ondulación de la curva; los términos pares(C,E, etc.) son simétricos en
x aplanando o afilando a la parábola, como se observa en la figura siguiente.
A
B
GE
C
0.0
X2
A=B=C=1
Las ecuaciones de Redlich-Kister proporcionan un método conveniente de
representación de los coeficientes de actividad de la fase líquida, y adicionalmente una
clasificación de los diferentes tipos de disoluciones líquidas. Las ecuaciones (1), (2) y
(3) se aplican a datos isotérmicos, pero con frecuencia se aplican a datos isobáricos,
siempre y cuando la temperatura no cambie mucho con la composición.
A partir de las ecuaciones (2) y (3) podemos obtener :
RT ln
1
 A( x2  x1 )  B (6 x1 x2  1)  C ( x1  x2 )(8 x1 x2  1)  D( x1  x2 ) 2 (10 x1 x2  1)  ... (4)
2
El número de parámetros requeridos en la ecuación (4) para representar los coeficientes
de actividad de una mezcla binaria es una indicación de la complejidad aparente de la
mezcla. Si el número de parámetros necesarios es elevado(4 o mas), la mezcla se puede
considerar compleja, si es reducido, la mezcla se considera simple.