1 Seminari 1. Estadística CP

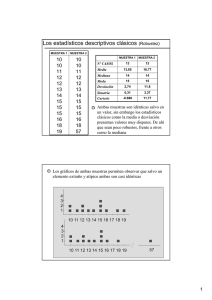
Seminari 1. Estadística CP
Problema 1.
Exercici
1.29 (pàgina 37 capítul 1 Moore – 2a edició)
Els més rics. A EEUU la distribució dels ingressos individuals és
molt esbiaixada cap a la dreta. En 1997 la mitja i la mitjana dels
ingressos de l’1% dels nord-americans més rics era de 330.000 i
676.000 dólars, respectivament. ¿Quin d’aquests valors correspon a la
mitja i quin a la mediana? Justifica la teva resposta.
La mediana és de 330.000 dòlars i la renta mitja és de 675.000
dòlars.
És una distribució esbiaixada cap a la dreta, el costat dret de la
distribució (el que conté la meitat de les observacions més grans)
s’estén molt més lluny que el costat esquerre.
La mitja és una mesura poc robusta en el sentit que és sensible a
observacions extremes i la mediana és una mesura de centre
robusta. En altres paraules, davant la presència d’observacions
inusualment elevades, la mitja també es veurà incrementada en
excés prenent en conseqüència un valor més gran que la mediana.
Així doncs, com en una distribució esbiaixada cap a la dreta la
mitja serà també desplaçada la dreta en extrem (però no la
mediana) concloem que 675.000 dòlars és el valor de la mitja i
330.000 dòlars el de la mediana.
1
Problema 2.
Ejercicio 1.40 Porcentaje del PIB destinado a educación (página 51
capitulo 1 Moore – 2a edición).
a) Haz una lista (con los valores ordenados) de los datos del
porcentaje del PIB destinado a educación pública de los Estados de la
Unión Europea y otra lista con los datos de los Estados de Este.
Estas dos listas son los dos conjuntos de datos que queremos comparar
En primer lugar debemos entrar los datos creando tres variables
que podemos llamar Estado, Región y PIB_ep.
Para crear dos listas separadas a partir del conjunto de datos
completo podemos utilizar el siguiente procedimiento, aunque no es
la única manera de resolver la cuestión.
Consideremos la secuencia DATOS + SELECCIONAR CASOS
Activar “Si se satisface la condición” y seleccionar “Si”, se
obtiene una nueva ventana.
Ponemos la variable “Región” en la ventanilla a la derecha y
escribimos =”UE” (también podemos escribir directamente
Región=”UE”). Fíjate que UE está escrito entre comillas porque no
se trata de un número, sino de una palabra.
2
Después de CONTINUAR obtenemos otra vez la ventana de antes y
seleccionamos “Copiar casos seleccionados a un nuevo conjunto de
datos” y ponemos un nombre como UE (por ejemplo). En la nueva
ventana que contiene solo los datos con Región igual a UE para
ordenar los casos hacemos DATOS + ORDENAR CASOS
y ponemos como
variable segundo la cual ordenar “PIB_EP”.
Hacemos el mismo procedimiento seleccionando Región=”EE” para
crear una lista que contenga solo los datos relativos a los Países
del Este.
(También
podemos
decidir
seleccionar
“Descartar
casos
no
seleccionados” o “Eliminar casos no seleccionados” bajo la opción
“Resultado”. En el primer caso la ventana de los datos nos muestra
todos los datos pero indica los datos no seleccionados con una
línea. También en este caso SPSS crea una variable filter que
puede tomar el valor de 1 o 0 si el caso es entre los
seleccionados o no. En el segundo caso SPSS elimina directamente
todos los casos no seleccionados. ¡Cuidado! Si el conjunto de
datos inicial no esta salvado, no se puede volver detrás).
b) Dibuja los gráficos y calcula resúmenes numéricos para comparar
ambas distribuciones. Describe brevemente lo que observas
Para comparar dos distribuciones podemos hacer histogramas
poniendo ‘porcentaje’ en el eje de Y O también diagramas de cajas.
Para dibujar el histograma seleccionamos GRAFICOS + INTERACTIVOS +
HISTOGRAMA. En asignar variables, desplazamos al eje Y
‘Porcentaje’ y en el eje X asignamos “PIB_ep”. En ‘Histograma’
podemos mantener la opción ‘Asignar automáticamente intervalos’.
En ‘Títulos’ ponemos “Unión Europea”. En ‘Opciones’ seleccionamos
‘Amplitud de la Escala/Variable’ como ‘Porcentaje’. Hacemos lo
mismo por el segundo conjunto de datos poniendo en ‘Títulos’
“Países del Este”. El resultado es,
3
Para dibujar el diagrama de caja seleccionamos GRAFICOS +
INTERACTIVOS + DIAGRAMA DE CAJA. En asignar variables, desplazamos
al eje Y la variable ‘PIB_ep’. En ‘Cajas’ podemos mantener activas
‘Valores atípicos’, ‘Extremos’ y ‘Línea de la mediana’. En
‘Títulos’ podemos escribir en ‘Título del grafico’ “Unión Europea”
“Países del Este”. Estos son los dos gráficos,
Como se puede ver los gráficos no tienen la misma escala. Para
obtener los dos gráficos de cajas en escalas comparables
directamente podemos utilizar el conjunto de datos inicial (con
todas las regiones), eliminar los casos por los cuales la variable
Región es igual a “OT” y hacer: ANALIZAR + ESTADISTICO DESCRIPTIVO
+ EXPLORAR; bajo ‘Dependientes’ poner ‘PIB_ep’ y bajo ‘factores’
poner ‘Región’. Seleccionamos solo el Diagrama de Caja y aquí está
el resultado (fijaos como parece distinto del grafico de antes aún
sea lo mismo):
4
Para calcular los resúmenes numéricos podemos hacer ANALIZAR +
ESTADISTICOS DESCRIPTIVOS + EXPLORAR. Ponemos ‘PIB_ep’ bajo
‘Dependientes’. Seleccionamos solo ‘Estadísticos’ y después
‘Estadísticos’ y ‘Descriptivos’.
Para los datos de la lista UE obtenemos,
5
Los descriptivos para los países de la lista EE son,
(En el ejercicio siguiente
resúmenes numéricos)
veremos
otro
modo
para
obtener
Interpretación. Los histogramas muestran una distribución más
simétrica en el caso de los Países de la Unión Europea y una
distribución ligeramente asimétrica hacia la izquierda en el caso
de los Países del Este. Para los Países de la Unión Europea, la
media y la mediana son muy cerca (5.9 y 5.8), mientras que para
los Países del Este la media es ligeramente inferior a la mediana
(5.6 y 5.8).
Los diagramas de cajas facilitan la comparación de las
distribuciones. Hay una dispersión menor en los datos de los
Países del Este en comparación a los Países de la Unión Europea.
De hecho varianza, rango (que es obtenido como el máximo menos el
mínimo) y rango intercuartiles son menores por los Países del
Este.
Fijaos también en el número de casos perdidos (en el primer
resumen numérico de cada grupo): 2 perdidos en el grupo UE
(Alemania y Luxemburgo) y 4 perdidos en el grupo EE (Albania,
Bosnia-Herzegovina, Croacia, Yugoslavia)
6
Problema 3.
Ejercicio 1.41 Densidad de la Tierra (página 52 capitulo 1 Moore – 2a
edición).
a) Representa gráficamente los datos de la manera que consideres más
conveniente.
En primer lugar debemos entrar los datos creando una variable que
podemos llamar “densidad”.
Para decidir el gráfico más conveniente tenemos que observar la
variable “densidad” es una variable cuantitativa continua. Podemos
representarla con un histograma, un diagrama de caja o también con
un gráfico de tallo y hojas (porque se trata de un conjunto pequeño
de datos). Vamos a dibujar los tres gráficos.
Para dibujar el gráfico de tallo y hojas debemos seleccionar
ANALIZAR + ESTADISTICOS DESCRIPTIVOS + EXPLORAR (seleccionar sólo
gráficos y desactivar todo excepto “Diagrama de tallo y hoja”)
Pulsamos CONTINUAR. En variable dependiente asignamos “densidad”.
Pulsamos ACEPTAR.
Obtenemos el siguiente grafico:
Para dibujar el histograma seleccionamos GRAFICOS + INTERACTIVOS +
HISTOGRAMA. En asignar variables, desplazamos al eje Y ‘Porcentaje’
y en el eje X asignamos “densidad”. En ‘Histograma’ podemos mantener
la opción ‘Asignar automáticamente intervalos’. En ‘Opciones’
seleccionamos ‘Amplitud de la Escala/Variable’ como ‘Porcentaje’. El
resultado es,
7
Podemos también poner ‘Recuento’ en el eje Y (en vez de Porcentaje’)
y obtener este grafico
Los dos gráficos tienen las mismas formas, solo cambia la variable
en el eje de las Y, siendo el porcentaje en el primer caso (o sea la
frecuencia relativa) y el recuento en el segundo caso (o sea la
frecuencia absoluta).
Para dibujar el diagrama de caja seleccionamos GRAFICOS +
INTERACTIVOS + DIAGRAMA DE CAJA. En asignar variables, desplazamos
al eje Y la variable ‘densidad’. En ‘Cajas’ podemos mantener activas
‘Valores atípicos’, ‘Extremos’ y ‘Línea de la mediana’. En ‘Títulos’
podemos escribir en ‘Título del grafico’ “Densidad de la Tierra”.
Este es el resultado,
8
Interpretación de los tres gráficos:
1.
centro: desde el diagrama de caja tenemos una medida clara del
centro, o sea la mediana que es del orden de 5,45. Los otros dos
gráficos confirman esta medida aproximada.
2.
simetría: la distribución es bastante simétrica. El histograma
y el diagrama de tallos no muestran colas a la derecha o a la
izquierda; en el diagrama de caja el primero y el tercero cuartil
están aproximadamente a la misma distancia de la mediana.
3.
observaciones atípicas: no hay observaciones atípicas (el
diagrama de caja no reporta ninguna observación atípica ni extrema)
b) La forma de la distribución ¿permite utilizar la media y la
desviación típica (s) para describirla? Halla media y desviación
típica
Si: para describir una distribución bastante simétrica que no
presenta observaciones atípicas, la media y la desviación típica son
buenas medidas de centro y de dispersión.
Para hallar media y desviación típica hacemos: ANALIZAR+ESTADISTICOS
DESCRIPTIVOS+ DESCRIPTIVOS+OPCIONES.
En la ventana que se abre podemos elegir diferentes estadísticos
descriptivos. Elegimos ‘Media’ y ‘Desv. típica’ y (para verlo una
vez)
también
‘Curtosis’
y
‘Asimetría’
(indicados
bajo
‘Distribución’).
9
Pulsamos CONTINUAR y pasamos ‘densidad’ a el campo ‘Variables’. El
resultado es el siguiente:
El coeficiente de asimetría (o skewness) y la curtosis son dos
estadísticos descriptivos que nos dan indicaciones sobre la simetría
y el grado de apuntamiento de una distribución (es decir la
concentración de datos alrededor de la media). Las formulas del
coeficiente de asimetría y de la curtosis utilizadas por SPSS son
las siguientes:
No es importante conocer estas formulas, pero pueden ser útiles para
medir la simetría de una distribución. El coeficiente de asimetría
es 0 para distribuciones perfectamente simétricas, menor que 0 para
distribuciones asimétricas hacia la izquierda y mayor que 0 para
distribuciones asimétricas hacia la derecha.
10
La distribución llamada normal, que conocemos del curso de
probabilidad, tiene coeficiente de curtosis igual a “0”. Si una
distribución tiene coeficiente de curtosis mayor que “0”, entonces
su forma es mas puntiaguda que la normal (hay una mayor
concentración de los datos en torno a la media). Si una distribución
tiene coeficiente de curtosis menor que “0”, entonces su forma es
más achatada que la normal (hay una menor concentración de los datos
en torno a la media).
En este caso, como ya hemos detectado de los gráficos, la
distribución es bastante simétrica. De hecho el coeficiente de
asimetría es negativo (ligera asimetría hacia la izquierda) pero muy
cerca de 0.
c) Teniendo en cuenta todo lo que acabas de hacer, ¿cuál es tu
estimación de la densidad de la Tierra a partir de estas mediciones?
Como las diferentes medidas obtenidas por Cavendish son distribuidas
simétricamente y sin observaciones atípicas, una buena estimación de
la densidad de la Tierra es la media de las 29 mediciones, es decir
5,4479 veces mayor que la densidad del agua.
11