Análisis de estructuras

UNIDAD
Análisis de estructuras
3.1.
UNIDAD 3
INTRODUCCION
L o s p r o b l e m a s c o n s i d e r a d o s e n las u n i d a d e s a n t e r i o r e s e s t u v i e r o n r e l a c i o n a d o s c o n e l e q u i l i b r i o d e u n s o l o c u e r p o rígido y t o d a s l a s f u e r z a s i n v o l u c r a d a s e r a n e x t e r n a s a e s t e último. A continuación s e e s t u d i a n p r o b l e m a s
q u e t r a t a n s o b r e e le q u i l i b r i o d e e s t r u c t u r a s f o r m a d a s p o r varias p a r t e s q u e
están c o n e c t a d a s e n t r e sí. E s t o s p r o b l e m a s , además d e d e t e r m i n a r l a s f u e r z a s e x t e r n a s q u e actúan s o b r e l a e s t r u c t u r a , i m p l i c a n c a l c u l a r l a s f u e r z a s q u e
m a n t i e n e n u n i d a s a las diversas p a r t e s q u e l a c o n s t i t u y e n . D e s d e e l p u n t o
d e v i s t a d e l a e s t r u c t u r a c o m o u n t o d o , e s t a s f u e r z a s s o n fuerzas
internas.
3.1 Introducción
3.2 Definición de una armadura
3.3 Armaduras simples
3.4 Análisis de armaduras por el
método de los nodos
3.5 Nodos bajo condiciones especiales
de carga
3.6 Análisis de armaduras por el
método de secciones
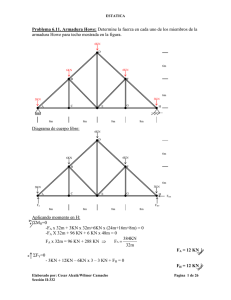
P o r e j e m p l o , c o n s i d é r e s e l a grúa m o s t r a d a e n l a figura 3 . 1 a ) , l a c u a l
s o p o r t a u n a c a r g a W. L a grúa c o n s t a d e t r e s v i g a s AD, CF y BE q u e están c o n e c t a d a s p o r m e d i o d e p e r n o s s i n fricción; l a grúa está a p o y a d a p o r u n p e r n o
e n A y u n c a b l e DG. L a figura 3.1¿>) r e p r e s e n t a e l d i a g r a m a d e c u e r p o l i b r e
d e l a grúa. L a s f u e r z a s e x t e r n a s q u e s e m u e s t r a n e n e l d i a g r a m a i n c l u y e n e l
p e s o W , l a s d o s c o m p o n e n t e s A y A ^ d e l a reacción e n A y l a f u e r z a T e j e r c i d a p o r e l c a b l e e n D. L a s f u e r z a s i n t e r n a s q u e m a n t i e n e n u n i d a s l a s d i v e r s a s
p a r t e s d e l a grúa n o a p a r e c e n e n e l d i a g r a m a . S i n e m b a r g o , s i s e d e s a r m a l a
grúa y s e d i b u j a u n d i a g r a m a d e c u e r p o l i b r e p a r a c a d a u n a d e l a s p a r t e s q u e
l a c o n s t i t u y e n , l a s f u e r z a s q u e m a n t i e n e n u n i d a s a l a s t r e s v i g a s también e s tarán r e p r e s e n t a d a s , p u e s t o q u e d i c h a s f u e r z a s s o n e x t e r n a s d e s d e e l p u n t o
d e v i s t a d e c a d a u n a d e l a s p a r t e s q u e f o r m a n l a grúa [ f i g u r a 3 . 1 c ) ] .
3.7 Armaduras formadas por varias
armaduras simples
3.8 Estructuras que contienen
elementos sujetos a fuerzas
múltiples
r
3.9 Análisis de un armazón
3.10 Armazones que dejan de ser rígidos
cuando se separan de sus soportes
3.11 Máquinas
3.12 Método del trabajo virtual
3.13 Principio del trabajo virtual
S e d e b e señalar q u e l a f u e r z a e j e r c i d a e n B p o r e l e l e m e n t o BE s o b r e e l e l e m e n t o AD s e h a r e p r e s e n t a d o c o m o i g u a l y o p u e s t a a l a f u e r z a e j e r c i d a e n e s e m i s m o p u n t o p o r e l e l e m e n t o AD s o b r e e l e l e m e n t o BE; l a f u e r z a
e j e r c i d a e n E p o r e l e l e m e n t o BE s o b r e e l e l e m e n t o CF s e m u e s t r a i g u a l y
o p u e s t a a l a f u e r z a e j e r c i d a p o r e l e l e m e n t o CF s o b r e e l e l e m e n t o BE y l a s
c o m p o n e n t e s d e l a f u e r z a e j e r c i d a e n C p o r e l e l e m e n t o CF s o b r e e l e l e m e n t o AD s e p r e s e n t a n i g u a l e s y o p u e s t a s a l a s c o m p o n e n t e s d e l a f u e r z a
e j e r c i d a p o r e l e l e m e n t o AD s o b r e e l e l e m e n t o CF. L o a n t e r i o r está s u j e t o a
l a t e r c e r a l e y d e N e w t o n , l a c u a l e s t a b l e c e q u e las fuerzas de acción y reacción entre cuerpos en contacto tienen la misma magnitud, la misma línea de
acción y sentidos opuestos. C o m o s e señaló e n l a u n i d a d 1 , e s t a l e y , q u e está
b a s a d a e n la e v i d e n c i a e x p e r i m e n t a l , e su n o d e los seis p r i n c i p i o s f u n d a m e n t a l e s d e l a m e c á n i c a e l e m e n t a l y s u aplicación e s e s e n c i a l p a r a l a solución d e
p r o b l e m a s q u e i n v o l u c r a n a c u e r p o s q u e están c o n e c t a d o s e n t r e sí.
3.14 Aplicaciones del principio del
trabajo virtual
Competencia específica
Analizar y resolver problemas que
impliquen estructuras planas.
D
D
a)
b)
D
c)
Figura 3.1
E n e s t a u n i d a d s e considerarán t r e s categorías a m p l i a s d e e s t r u c t u r a s
d e ingeniería:
154
1 . Armaduras, l a s c u a l e s están diseñadas p a r a s o p o r t a r c a r g a s y p o r l o g e n e r a l s o n e s t r u c t u r a s e s t a c i o n a r i a s q u e están t o t a l m e n t e r e s t r i n g i d a s .
Las a r m a d u r a s consisten exclusivamente e nelementos rectos q u e están c o n e c t a d o s e n n o d o s l o c a l i z a d o s e n l o s e x t r e m o s d e c a d a e l e m e n t o .
P o r t a n t o , l o s e l e m e n t o s d e u n a a r m a d u r a s o n elementos sujetos a dos
fuerzas, e s t o e s , e l e m e n t o s s o b r e l o s c u a l e s actúan d o s f u e r z a s i g u a l e s y
o p u e s t a s q u e están d i r i g i d a s a l o l a r g o d e l e l e m e n t o .
2 . Armazones, l o s c u a l e s están diseñados p a r a s o p o r t a r c a r g a s , s e u s a n t a m bién c o m o e s t r u c t u r a s e s t a c i o n a r i a s q u e están t o t a l m e n t e r e s t r i n g i d a s .
S i n e m b a r g o , c o m o e n e l c a s o d e l a grúa d e l a figura 3 . 1 , l o s a r m a z o n e s
s i e m p r e c o n t i e n e n p o r l o m e n o s u n elemento sujeto a varias fuerzas, e s t o
e s , u n e l e m e n t o s o b r e e l c u a l actúan t r e s o más f u e r z a s q u e , e n g e n e r a l ,
n o están d i r i g i d a s a l o l a r g o d e l e l e m e n t o .
3 . Máquinas, l a s c u a l e s están diseñadas p a r a t r a n s m i t i r y m o d i f i c a r f u e r z a s ,
s o n e s t r u c t u r a s q u e c o n t i e n e n p a r t e s e n m o v i m i e n t o . L a s máquinas, a l
igual q u e los a r m a z o n e s , s i e m p r e c o n t i e n e n p o r lo m e n o s u n e l e m e n t o
sujeto a varias fuerzas.
ARMADURAS
3.2. DEFINICIÓN DE UNA ARMADURA
L a a r m a d u r a es u n o d elos principales tipos d eestructuras q u e s eu s a n e n l a
ingeniería. E s t a p r o p o r c i o n a u n a solución práctica y e c o n ó m i c a p a r a m u c h a s
s i t u a c i o n e s d e ingeniería, e n e s p e c i a l p a r a e l diseño d e p u e n t e s y e d i f i c i o s .
E n l a figura 3 . 2 a ) s e m u e s t r a u n a a r m a d u r a típica. U n a a r m a d u r a c o n s t a d e
e l e m e n t o s rectos q u e s e c o n e c t a n e nn o d o s . L o s e l e m e n t o s d e l a a r m a d u r a
sólo están c o n e c t a d o s e n s u s e x t r e m o s ; p o r t a n t o , ningún e l e m e n t o continúa
más allá d e u n n o d o . P o r e j e m p l o , e n l a figura 3 . 2 a ) n o e x i s t e u n e l e m e n t o
AB, s i n o q u e e n s u l u g a r e x i s t e n d o s e l e m e n t o s d i s t i n t o s AD y DB. L a m a y o ría d e l a s e s t r u c t u r a s r e a l e s están h e c h a s a p a r t i r d e v a r i a s a r m a d u r a s u n i d a s
e n t r e sí p a r a f o r m a r u n a a r m a d u r a e s p a c i a l . C a d a a r m a d u r a está diseñada
p a r a s o p o r t a r a q u e l l a s c a r g a s q u e actúan e n s u p l a n o y , p o r t a n t o , p u e d e n s e r
tratadas c o m o estructuras bidimensionales.
L o s e l e m e n t o s d e u n a a r m a d u r a , p o r l o g e n e r a l , s o n d e l g a d o s y sólo
p u e d e n s o p o r t a r c a r g a s l a t e r a l e s pequeñas; p o r e s o t o d a s l a s c a r g a s d e b e n
estar aplicadas e n los n o d o s y n o sobre los e l e m e n t o s . C u a n d o s ev a a aplicar u n a carga concentrada e n t r e dos n o d o s o c u a n d o l aa r m a d u r a d e b e soportar u n a carga distribuida, c o m o e n e lcaso d ela a r m a d u r a d eu n p u e n t e ,
debe proporcionarse u n sistema de piso, el cual, mediante el uso de travesanos y largueros, t r a n s m i t e la carga a los nodos (figura 3.3).
L o s p e s o s d e l o s e l e m e n t o s d e l a a r m a d u r a l o s c a r g a n l o s n o d o s , aplicándose l am i t a d d e l p e s o d e cada e l e m e n t o a cada u n o d elos n o d o s a los q u e
éste s e c o n e c t a . A p e s a r d e q u e e n r e a l i d a d l o s e l e m e n t o s están u n i d o s e n t r e
sí p o r m e d i o d e c o n e x i o n e s r e m a c h a d a s o s o l d a d a s , e s c o m ú n s u p o n e r q u e
l o s e l e m e n t o s están c o n e c t a d o s p o r m e d i o d e p e r n o s ; p o r t a n t o , l a s f u e r z a s
q u e actúan e n c a d a u n o d e l o s e x t r e m o s d e l e l e m e n t o s e r e d u c e n a u n a s o l a
f u e r z a y n o e x i s t e u n p a r . D e e s t a f o r m a s e s u p o n e q u e l a s únicas f u e r z a s
Figura 3.2
156
Análisis de estructuras
q u e actúan s o b r e u n e l e m e n t o d e l a a r m a d u r a s o n u n a s o l a f u e r z a e n c a d a
u n o d elos e x t r e m o s d e l e l e m e n t o . E n t o n c e s , cada e l e m e n t o p u e d e tratarse
c o m o s o m e t i d o a l a acción d e d o s f u e r z a s , m i e n t r a s q u e l a a r m a d u r a , c o m o
u n todo, p u e d e considerarse que esu n g r u p o de pernos y elementos sujetos a
d o s f u e r z a s [ f i g u r a 3.2b)]. S o b r e u n e l e m e n t o i n d i v i d u a l p u e d e n a c t u a r f u e r z a s , c o m o l a s q u e s e m u e s t r a n e n c u a l q u i e r a d e l o s c r o q u i s d e l a figura 3 . 4 .
E n l a figura 3 . 4 a ) l a s f u e r z a s t i e n d e n a e s t i r a r a l e l e m e n t o y éste s e h a l l a e n
tensión; e n l a figura 3.4b) l a s f u e r z a s t i e n d e n a c o m p r i m i r a l e l e m e n t o q u e
está e n compresión. E n l a figura 3 . 5 s e m u e s t r a n a l g u n a s a r m a d u r a s típicas.
Pratt
Fink
Howe
A r m a d u r a s típicas p a r a t e c h o
Pratt
Warren
Howe
Armadura K
Baltimore
A r m a d u r a s típicas p a r a p u e n t e s
Parte de una armadura
en voladizo
Estadio
Figura 3.5
Basculante
Otros tipos de armaduras
3.3. ARMADURAS SIMPLES
Fotografía 3.2 Dos armaduras K se usaron
como los principales componentes del puente
móvil que se muestra en la foto, el cual se movía
por encima de un gran montón de mineral de
reserva. El cubo que se encuentra debajo de las
armaduras levantaba mineral y lo redeposltaba
hasta que el mineral estuvo completamente
mezclado. Después, el mineral se envió al molino
para incorporarlo a un proceso de producción de
acero.
C o n s i d e r e l a a r m a d u r a m o s t r a d a e n l a figura 3 . 6 a ) , l a c u a l está c o n s t i t u i d a
p o r c u a t r o e l e m e n t o s c o n e c t a d o s p o r m e d i o d e p e r n o s e n A, B, C y D. S i s e
a p l i c a u n a c a r g a e n B, l a a r m a d u r a s e deformará h a s t a p e r d e r p o r c o m p l e t o
s u f o r m a o r i g i n a l . P o r e l c o n t r a r i o , l a a r m a d u r a d e l a figura 3.6b), l a c u a l está
c o n s t i t u i d a p o r t r e s e l e m e n t o s c o n e c t a d o s p o r m e d i o d e p e r n o s e n A, B y C,
sólo s e d e f o r m a r á l i g e r a m e n t e b a j o l a acción d e u n a c a r g a a p l i c a d a e n B. L a
única d e f o r m a c i ó n p o s i b l e p a r a e s t a a r m a d u r a e s l a q u e i n v o l u c r a p e q u e ñ o s
c a m b i o s e n la l o n g i t u d d esus e l e m e n t o s . P o r t a n t o , se dice q u e la a r m a d u r a
d e l a figura 3.6¿>) e s u n a armadura rígida; aquí e l t é r m i n o rígida s e h a e m p l e a d o p a r a i n d i c a r q u e l a a r m a d u r a no se
colapsard.
C o m o s e m u e s t r a e n l a figura 3 . 6 c ) , s e p u e d e o b t e n e r u n a a r m a d u r a
rígida más g r a n d e s i s e a g r e g a n d o s e l e m e n t o s BD y CD a l a a r m a d u r a t r i a n g u l a r básica d e l a figura 3.6b). E s t e p r o c e d i m i e n t o s e p u e d e r e p e t i r t a n t a s
v e c e s c o m o s e d e s e e y l a a r m a d u r a r e s u l t a n t e será rígida s i c a d a v e z q u e s e
a g r e g a n d o s n u e v o s e l e m e n t o s , éstos s e u n e n a d o s n o d o s y a e x i s t e n t e s y
además s e c o n e c t a n e n t r e sí e n u n n u e v o n o d o . * U n a a r m a d u r a q u e s e p u e d e c o n s t r u i r d e e s t a f o r m a r e c i b e e l n o m b r e d e armadura
simple.
1
L o s tres n o d o s n o d e b e n ser colineales.
S e d e b e señalar q u e u n a a r m a d u r a s i m p l e n o e s t a h e c h a n e c e s a n a m e n i
. .,
i
t ,
í
i
i
i
i
c
n
n
3
4
A n á | | S I S d e
j\
e l
t e a p a r t i r d e triángulos. P o r e j e m p l o , l a a r m a d u r a d e l a f i g u r a ó.od) e s u n a
a r m a d u r a s i m p l e q u e f u e c o n s t r u i d a a p a r t i r d e l triángulo ABC y s e a g r e g a r o n s u c e s i v a m e n t e l o s n o d o s D,E,Fy
G. P o r o t r a p a r t e , l a s a r m a d u r a s rígidas n o s i e m p r e son a r m a d u r a s simples, incluso c u a n d o p a r e c e n estar hechas
d e triángulos. P o r e j e m p l o , l a s a r m a d u r a s d e F i n k y B a l t i m o r e m o s t r a d a s
e n l a figura 3 . 5 n o s o n a r m a d u r a s s i m p l e s , p u e s t o q u e n o p u e d e n c o n s t r u i r s e a p a r t i r d e u n s o l o triángulo e n l a f o r m a d e s c r i t a e n e l párrafo a n t e r i o r .
T o d a s l a s demás a r m a d u r a s q u e s e m u e s t r a n e n l a figura 3 . 5 s o n a r m a d u r a s
s i m p l e s , l o c u a l s e p u e d e v e r i f i c a r fácilmente. ( P a r a l a a r m a d u r a K s e d e b e
c o m e n z a r c o n u n o d e l o s triángulos c e n t r a l e s . )
a)
b)
c)
armaduras por
método de los nodos
d)
Figura 3.6
E n l a figura 3 . 6 s e o b s e r v a q u e l a a r m a d u r a t r i a n g u l a r básica d e l a
figura
3 . 6 ¿ ) t i e n e t r e s e l e m e n t o s y t r e s n o d o s . L a a r m a d u r a d e l a figura 3 . 6 c ) t i e ne dos elementos y u n n o d o adicionales, esto es,cinco elementos y cuatro
n o d o s e n total. S isetiene presente q u e cada vez q u e se agregan dos n u e v o s
e l e m e n t o s e l número d e n o d o s s e i n c r e m e n t a e n u n o , s e e n c u e n t r a q u e e n
u n a a r m a d u r a s i m p l e e l número t o t a l d e e l e m e n t o s e s m = 2 n — 3 , d o n d e n
es e l número t o t a l d e n o d o s .
3.4. ANALISIS DE ARMADURAS POR EL METODO
DE LOS NODOS
E n l a sección 3 . 2 s e v i o q u e u n a a r m a d u r a p u e d e s e r c o n s i d e r a d a c o m o u n
g r u p o d e p e r n o s y e l e m e n t o s s o m e t i d o s a l a acción d e d o s f u e r z a s . P o r t a n t o ,
l a a r m a d u r a d e l a figura 3 . 2 , c u y o d i a g r a m a d e c u e r p o l i b r e s e m u e s t r a e n l a
figura
3.7a), sep u e d e desarmar y dibujar u n diagrama d ecuerpo libre para
c a d a p e r n o y p a r a c a d a e l e m e n t o [ f i g u r a 3.7b)]. C a d a e l e m e n t o está s o m e t i d o a l a acción d e d o s f u e r z a s , u n a e n c a d a u n o d e s u s e x t r e m o s ; e s t a s f u e r z a s
t i e n e n l a m i s m a m a g n i t u d , l a m i s m a línea d e acción y s e n t i d o s o p u e s t o s
(sección 2 . 2 6 ) . A d e m á s , l a t e r c e r a l e y d e N e w t o n i n d i c a q u e l a s f u e r z a s d e
acción y reacción e n t r e u n e l e m e n t o y u n p e r n o s o n i g u a l e s y o p u e s t a s . P o r
t a n t o , las f u e r z a s e j e r c i d a s p o r u n e l e m e n t o s o b r e los d o s p e r n o s a los c u a les s e c o n e c t a d e b e n estar dirigidas a l o l a r g o d ee s ee l e m e n t o y d e b e n ser
i g u a l e s y o p u e s t a s . C o n f r e c u e n c i a s e h a c e r e f e r e n c i a a l a m a g n i t u d común
d e las f u e r z a s e j e r c i d a s p o r u n e l e m e n t o s o b r e los d o s p e r n o s a los q u e s e con e c t a c o m o l a fuerza en el elemento b a j o consideración, a p e s a r d e q u e e s t a
c a n t i d a d e n r e a l i d a d e s u n e s c a l a r . C o m o l a s líneas d e acción d e t o d a s l a s
f u e r z a s i n t e r n a s e n u n a a r m a d u r a s o n c o n o c i d a s , e l análisis d e u n a a r m a d u r a
se r e d u c e a c a l c u l a r las f u e r z a s e nlos e l e m e n t o s q u e l ac o n s t i t u y e n y a d e t e r m i n a r s i c a d a u n o d e d i c h o s e l e m e n t o s está e n tensión o e n compresión.
C o m o l a a r m a d u r a e n s u t o t a l i d a d está e n e q u i l i b r i o , c a d a p e r n o d e b e
e s t a r e n e q u i l i b r i o . E l q u e u n p e r n o esté e n e q u i l i b r i o s e e x p r e s a d i b u j a n d o
s u d i a g r a m a d e c u e r p o l i b r e y e s c r i b i e n d o dos e c u a c i o n e s d e e q u i l i b r i o (sec-
a)
b)
Figura 3.7
- j 5y
-J
Análisis de estructuras
ción 1 . 1 2 ) . P o r t a n t o , s i u n a a r m a d u r a t i e n e n p e r n o s , habrá 2 n e c u a c i o n e s
d i s p o n i b l e s , l a s c u a l e s podrán r e s o l v e r s e p a r a 2 n incógnitas. E n e l c a s o d e
u n a a r m a d u r a s i m p l e , s e t i e n e q u e m = 2n — 3 , e s t o e s , 2 n = m + 3 , y e l
n ú m e r o d e incógnitas q u e s e p u e d e n d e t e r m i n a r a p a r t i r d e l o s d i a g r a m a s d e
c u e r p o l i b r e d e los p e r n o s e s m + 3 . E s t o significa q u e las f u e r z a s e n t o d o s
l o s e l e m e n t o s , l a s d o s c o m p o n e n t e s d e l a reacción R y l a reacción R s e
d e t e r m i n a n al considerar los diagramas d ec u e r p o l i b r e d elos pernos.
E l h e c h o d e q u e l a a r m a d u r a c o m o u n t o d o s e a u n c u e r p o rígido q u e
está e n e q u i l i b r i o s e p u e d e u t i l i z a r p a r a e s c r i b i r t r e s e c u a c i o n e s a d i c i o n a l e s
q u e i n v o l u c r a n a las f u e r z a s m o s t r a d a s e ne ld i a g r a m a d ec u e r p o l i b r e d e l a
figura
3 . 7 a ) . P u e s t o q u e e s t a s e c u a c i o n e s n o c o n t i e n e n n i n g u n a información
nueva, son independientes d e lasecuaciones asociadas c o n los diagramas
d e c u e r p o l i b r e d e l o s p e r n o s . S i n e m b a r g o , l a s t r e s e c u a c i o n e s e n cuestión
se p u e d e n e m p l e a r p a r a d e t e r m i n a r las c o m p o n e n t e s d e las r e a c c i o n e s e n
los apoyos. E l a r r e g l o d ep e r n o s y e l e m e n t o s e n u n a a r m a d u r a s i m p l e es tal
q u e s i e m p r e será p o s i b l e e n c o n t r a r u n n o d o q u e i n v o l u c r e ú n i c a m e n t e a
d o s f u e r z a s d e s c o n o c i d a s . E s t a s f u e r z a s s e d e t e r m i n a n p o r m e d i o d e l o s mét o d o s d e l a sección 1 . 1 4 y s u s v a l o r e s s e t r a n s f i e r e n a l o s n o d o s a d y a c e n t e s
tratándolos c o m o c a n t i d a d e s c o n o c i d a s e n d i c h o s n o d o s ; e s t e p r o c e d i m i e n t o
se r e p i t e h a s t a d e t e r m i n a r t o d a s las f u e r z a s d e s c o n o c i d a s .
C o m o e j e m p l o s e a n a l i z a l a a r m a d u r a d e l a figura 3 . 7 , e n l a q u e s e c o n s i d e r a s u c e s i v a m e n t e e le q u i l i b r i o d ec a d a p e r n o ; se i n i c i a c o n e ln o d o e n e l
c u a l sólo d o s f u e r z a s s o n d e s c o n o c i d a s . E n d i c h a a r m a d u r a t o d o s l o s p e r n o s
están s u j e t o s p o r l o m e n o s t r e s f u e r z a s d e s c o n o c i d a s . P o r t a n t o , p r i m e r o s e
d e b e n d e t e r m i n a r las r e a c c i o n e s e n los a p o y o s c o n s i d e r a n d o a t o d a l a arm a d u r a c o m o c u e r p o l i b r e y u t i l i z a n d o las e c u a c i o n e s d ee q u i l i b r i o p a r a u n
c u e r p o rígido. D e e s t a f o r m a , R e s v e r t i c a l y s e d e t e r m i n a n l a s m a g n i t u d e s
deR yR .
E n t o n c e s e l número d e f u e r z a s d e s c o n o c i d a s e n e l n o d o A s e r e d u c e
a dos y estas fuerzas se p u e d e n d e t e r m i n a r s ise considera e le q u i l i b r i o d e l
p e r n o A. L a reacción R y l a s f u e r z a s F
y F
ejercidas sobre e lp e r n o A
p o r l o s e l e m e n t o s AC y AD, r e s p e c t i v a m e n t e , d e b e n f o r m a r u n triángulo d e
fuerzas. P r i m e r o se d i b u j a R (figura 3.8); luego, s iF
yF
están d i r i g i d a s
a l o l a r g o d e AC y AD, r e s p e c t i v a m e n t e , s e c o m p l e t a e l triángulo d e f u e r z a s
y se d e t e r m i n a n la m a g n i t u d y el s e n t i d o d eF
y F . Las magnitudes F
y
F
r e p r e s e n t a n l a s f u e r z a s e n l o s e l e m e n t o s AC y AD. C o m o F , está d i r i g i d a h a c i a a b a j o y h a c i a l a i z q u i e r d a , e s t o e s , hacia e l n o d o A , e l e l e m e n t o AC
e m p u j a e l p e r n o A y, p o r c o n s i g u i e n t e , d i c h o e l e m e n t o está e n compresión.
Como F
está d i r i g i d a alejándose
d e l n o d o A , e l e l e m e n t o AD j a l a e l p e r n o
A y , p o r c o n s i g u i e n t e , d i c h o e l e m e n t o está e n tensión.
A h o r a s e p r o c e d e a c o n s i d e r a r e l n o d o D e n e l c u a l sólo d o s f u e r z a s ,
F . y F , aún s o n d e s c o n o c i d a s . L a s o t r a s f u e r z a s q u e actúan s o b r e d i c h o
n o d o s o n l a c a r g a P, l a c u a l e s u n d a t o , y l a f u e r z a ¥
ejercida sobre e l pern o p o r e l e l e m e n t o AD. C o m o s e señaló a n t e s , e s t a última f u e r z a e s i g u a l y
opuesta a lafuerza F
e j e r c i d a p o r e l m i s m o e l e m e n t o s o b r e e l p e r n o A.
C o m o s e m u e s t r a e n l a figura 3 . 8 , s e p u e d e d i b u j a r e l polígono d e f u e r z a s
c o r r e s p o n d i e n t e a l n o d o D y d e t e r m i n a r las f u e r z a s F
y F
a partir d e
d i c h o polígono. S i n e m b a r g o , c u a n d o están i n v o l u c r a d a s más d e t r e s f u e r z a s ,
e s más c o n v e n i e n t e r e s o l v e r l a s e c u a c i o n e s d e e q u i l i b r i o 2 F = 0 y E F ^ = 0
p a r a las d o s f u e r z a s d e s c o n o c i d a s . C o m o s e e n c u e n t r a q u e a m b a s f u e r z a s s e
a l e j a n d e l n o d o D, l o s e l e m e n t o s DC y DB j a l a n e l p e r n o y s e c o n c l u y e q u e
a m b o s están e n tensión.
Después s e c o n s i d e r a e l n o d o C , c u y o d i a g r a m a d e c u e r p o l i b r e s e
m u e s t r a e n l a figura 3 . 8 . S e o b s e r v a q u e t a n t o F
como F
son conocidas
a p a r t i r d e l análisis d e l o s n o d o s a n t e r i o r e s y q u e sólo F
es desconocida.
C o m o e l e q u i l i b r i o d e c a d a p e r n o p r o p o r c i o n a s u f i c i e n t e información p a r a
d e t e r m i n a r d o s incógnitas, s e o b t i e n e u n a c o m p r o b a c i ó n d e l análisis r e a l i z a A
Fotografía 3.3 Las armaduras para techo, como
las que se muestran en la foto, requieren apoyo
sólo en los extremos. Gracias a esto es posible
realizar construcciones con grandes áreas libres
de obstáculos en el piso.
B
A
A
f
l
A
A C
A D
4
A C
A C
A D
A D
AC
A (
AD
AÜ
D f
D B
D A
A D
D C
D B
x
r
D
C 4
C B
d o e n e s t e n o d o . S e d i b u j a e l triángulo d e f u e r z a s y s e d e t e r m i n a l a m a g n i tud y el sentido d e F . C o m o F
está d i r i g i d a h a c i a e l n o d o C , e l e l e m e n t o
CB e m p u j a e l p e r n o C y , p o r t a n t o , está e n c o m p r e s i ó n . L a c o m p r o b a c i ó n s e
obtiene al verificar que la fuerza F
y e l e l e m e n t o CB s o n p a r a l e l o s .
C B
C B
~
~
C B
E n e ln o d o B t o d a s las f u e r z a s s o n c o n o c i d a s . P u e s t o q u e e lp e r n o c o r r e s p o n d i e n t e está e n e q u i l i b r i o , e l triángulo d e f u e r z a s d e b e c e r r a r , y s e
o b t i e n e d e e s t a f o r m a u n a c o m p r o b a c i ó n a d i c i o n a l d e l análisis r e a l i z a d o .
E s i m p o r t a n t e señalar q u e l o s polígonos d e f u e r z a m o s t r a d o s e n l a fig u r a 3 . 8 n o s o n únicos. C a d a u n o d e e l l o s podría r e e m p l a z a r s e p o r u n a
configuración a l t e r n a . P o r e j e m p l o , e l triángulo d e f u e r z a s c o r r e s p o n d i e n t e
a l n o d o A podría d i b u j a r s e c o m o e l d e l a figura 3 . 9 . E l triángulo m o s t r a d o
e n l a figura 3 . 8 s e o b t u v o a l d i b u j a r l a s t r e s f u e r z a s R , F
y F
uniendo
la p a r t e t e r m i n a l d e u n a c o n l ap a r t e i n i c i a l d e o t r a , e ne l o r d e n e nq u e s e
e n c u e n t r a n s u s líneas d e acción, a l r e a l i z a r u n d e s p l a z a m i e n t o e n e l s e n t i d o
d e l m o v i m i e n t o d e l a s m a n e c i l l a s d e l r e l o j , a l r e d e d o r d e l n o d o A. L o s o t r o s
polígonos d e f u e r z a s e n l a figura 3 . 8 s e d i b u j a r o n d e l a m i s m a f o r m a ; p o r
e l l o , s e p u e d e n r e u n i r e n u n s o l o d i a g r a m a , c o m o s e i l u s t r a e n l a figura 3 . 1 0 .
U n d i a g r a m a d e e s t e t i p o , c o n o c i d o c o m o diagrama de Maxwell, f a c i l i t a e n
g r a n m e d i d a e l análisis gráfico d e p r o b l e m a s q u e i n v o l u c r a n a r m a d u r a s .
A
A C
Figura 3.9
A D
Figura 3.10
7
160
Análisis de estructuras
3.5. NODOS BAJO CONDICIONES ESPECIALES DE CARGA
O b s e r v e l a figura 3 . 1 1 a ) , e n l a c u a l e l n o d o c o n e c t a a c u a t r o e l e m e n t o s q u e
están u b i c a d o s s o b r e d o s líneas r e c t a s q u e s e i n t e r s e c a n . E l d i a g r a m a d e
c u e r p o l i b r e d e l a figura 3 . U f e ) m u e s t r a q u e e l p e r n o A está s u j e t o a d o s
p a r e s d e f u e r z a s d i r e c t a m e n t e o p u e s t a s . P o r t a n t o , e l polígono d e f u e r z a s
d e b e s e r u n p a r a l e l o g r a m o [ f i g u r a 3 . 1 1 c ) ] y las fuerzas en elementos
opuestos
deben ser iguales.
a)
b)
c)
Figura 3.11
A continuación c o n s i d e r e l a figura 3 . 1 2 a ) , e n l a c u a l e l n o d o m o s t r a d o c o n e c t a t r e s e l e m e n t o s y s o p o r t a u n a c a r g a P. D o s d e l o s e l e m e n t o s s e
e n c u e n t r a n u b i c a d o s s o b r e l a m i s m a línea y l a c a r g a P actúa a l o l a r g o d e l
t e r c e r e l e m e n t o . E l d i a g r a m a d e c u e r p o l i b r e d e l p e r n o A y e l polígono d e
f u e r z a s c o r r e s p o n d i e n t e serán c o m o s e m u e s t r a n e n l a f i g u r a 3.11¿>) y e ) , r e emplazando aF
p o r l a c a r g a P. P o r t a n t o , las fuerzas en los dos
elementos
opuestos deben ser iguales y la fuerza en el otro elemento debe ser igual a P.
E n l a figura 3 . 1 2 Z ? ) s e m u e s t r a u n c a s o d e e s p e c i a l interés, e n e l q u e n o h a y
u n a f u e r z a e x t e r n a a p l i c a d a e n e l n o d o , s e t i e n e q u e P = 0, y l a f u e r z a e n e l
e l e m e n t o AC e s i g u a l a c e r o . P o r t a n t o , s e d i c e q u e e l e l e m e n t o AC e s u n
elemento de fuerza
cero.
A £
Figura 3.12
C o n s i d e r e a h o r a u n n o d o q u e c o n e c t a sólo d o s e l e m e n t o s . A p a r t i r d e l a
sección 1 . 1 2 s e s a b e q u e u n a partícula s o b r e l a q u e actúan d o s f u e r z a s estará
e n e q u i l i b r i o s i l a s d o s f u e r z a s t i e n e n l a m i s m a m a g n i t u d , l a m i s m a línea d e
acción y s e n t i d o s o p u e s t o s . E n e l c a s o d e l n o d o d e l a figura 3 . 1 3 a ) , e l c u a l
c o n e c t a a d o s e l e m e n t o s AB y AD q u e s e e n c u e n t r a n s o b r e l a m i s m a línea,
las fuerzas en los dos elementos deben ser iguales p a r a q u e e l p e r n o A esté
e n e q u i l i b r i o . E n e l c a s o d e l n o d o d e l a figura 3 . 1 3 ¿ ) , e l p e r n o A n o p u e d e
estar e n e q u i l i b r i o a m e n o s q u e las f u e r z a s e n a m b o s e l e m e n t o s s e a n iguales
a cero. P o r tanto, los e l e m e n t o s conectados c o m o s e m u e s t r a e n l a
figura
3 . 1 3 ¿ ) d e b e n s e r elementos de fuerza
cero.
i
3.5 Nodos bajo condiciones especiales
de carga
/ /
b)
L a identificación d e l o s n o d o s q u e s e e n c u e n t r a n b a j o l a s c o n d i c i o n e s
e s p e c i a l e s d e c a r g a m e n c i o n a d a s e n l o s párrafos a n t e r i o r e s permitirá q u e e l
análisis d e u n a a r m a d u r a s e l l e v e a c a b o m á s rápido. P o r e j e m p l o , c o n s i d e r e
u n a a r m a d u r a t i p o H o w e cargada, c o m o s em u e s t r a e n l afigura 3.14; t o d o s
l o s e l e m e n t o s r e p r e s e n t a d o s p o r líneas e n c o l o r serán r e c o n o c i d o s c o m o
e l e m e n t o s d e f u e r z a cero. E l n o d o C conecta a tres e l e m e n t o s , dos d e los
c u a l e s s e e n c u e n t r a n s o b r e l a m i s m a línea y n o está s u j e t o a c a r g a s e x t e r n a s ;
p o r t a n t o , e l e l e m e n t o BC e s u n e l e m e n t o d e f u e r z a c e r o . S i s e a p l i c a e l m i s m o r a z o n a m i e n t o a l n o d o K, s e e n c u e n t r a q u e e l e l e m e n t o JK t a m b i é n e s u n
e l e m e n t o d e f u e r z a c e r o . A h o r a , e l n o d o J está e n l a m i s m a situación q u e l o s
n o d o s C y K; e n t o n c e s e l e l e m e n t o IJ d e b e s e r u n e l e m e n t o d e f u e r z a c e r o .
L a observación d e l o s n o d o s C , J y K r e v e l a q u e l a s f u e r z a s e n l o s e l e m e n t o s
AC y CE s o n i g u a l e s l a s f u e r z a s e n l o s e l e m e n t o s HJ y JL s o n t a m b i é n i g u a l e s , así c o m o l a s f u e r z a s e n l o s e l e m e n t o s IK y KL. R e g r e s a n d o l a atención a l
n o d o I, d o n d e l a c a r g a d e 2 0 k N y e l e l e m e n t o HI s o n c o l i n e a l e s , s e o b s e r v a
q u e l a f u e r z a e n e l e l e m e n t o HI e s d e 2 0 k N (tensión) y q u e l a s f u e r z a s e n l o s
e l e m e n t o s Gl e IK s o n i g u a l e s . D e e s t a m a n e r a , s e c o n c l u y e q u e l a s f u e r z a s
e n l o s e l e m e n t o s GI, IK y KL s o n i g u a l e s .
Fotografía 3.4 Las armaduras
tridimensionales o espaciales se usan para
las torres de transmisión de energía eléctrica
y señales en estructuras de techo y para
aplicaciones a naves espaciales, como en
los componentes de la Estación
Internacional.
25 k N |
25 k N
\
\
50 k N
i
" o
J
20 k N r
1
I
Figura 3.14
S e d e b e o b s e r v a r q u e l a s c o n d i c i o n e s d e s c r i t a s e n e l párrafo a n t e r i o r n o
p u e d e n a p l i c a r s e a l o s n o d o s B y D d e l a figura 3 . 1 4 y sería e r r ó n e o s u p o n e r
q u e l a f u e r z a e n e l e l e m e n t o DE e s d e 2 5 k N o q u e l a s f u e r z a s e n l o s e l e m e n t o s AB y BD s o n i g u a l e s . L a s f u e r z a s e n e s t o s e l e m e n t o s y e n l o s r e s t a n t e s s e e n c u e n t r a n c o n e l análisis d e l o s n o d o s A , B, D, E, F, G, H y L e n l a
f o r m a h a b i t u a l . P o r t a n t o , h a s t a q u e s e esté f a m i l i a r i z a d o c o n l a s c o n d i c i o n e s
q u e p e r m i t e n a p l i c a r l a s r e g l a s e s t a b l e c i d a s e n e s t a sección, s e d e b e d i b u j a r
el d i a g r a m a d e c u e r p o l i b r e d e t o d o s los p e r n o s y e s c r i b i r las e c u a c i o n e s d e
e q u i l i b r i o c o r r e s p o n d i e n t e s ( o d i b u j a r l o s polígonos d e f u e r z a s c o r r e s p o n d i e n t e s ) s i n i m p o r t a r s ilos m e d i o s c o n s i d e r a d o s s ee n c u e n t r a n b a j o u n a d e
las c o n d i c i o n e s e s p e c i a l e s d ec a r g a q u e s e d e s c r i b i e r o n a n t e r i o r m e n t e .
U n c o m e n t a r i o final e n relación c o n l o s e l e m e n t o s d e f u e r z a c e r o : e s t o s
e l e m e n t o s n o s o n inútiles. P o r e j e m p l o , a p e s a r d e q u e l o s e l e m e n t o s d e
f u e r z a c e r o d e l a figura 3 . 1 4 n o s o p o r t a n n i n g u n a c a r g a b a j o l a s c o n d i c i o n e s
m o s t r a d a s , e s p r o b a b l e q u e l o s m i s m o s e l e m e n t o s podrían s o p o r t a r a l g u n a
s i s e c a m b i a r a n l a s c o n d i c i o n e s d e c a r g a . Además, i n c l u s o e n e l c a s o c o n s i derado, estos e l e m e n t o s son necesarios p a r a soportar el peso de la a r m a d u r a
y p a r a m a n t e n e r a e s t a última c o n l a f o r m a d e s e a d a .
Espacial
2 0 0 0 Ib
1 000 Ib
t
l 2 ft
,
2 000 Ib
PROBLEMA RESUELTO 3.1
1 2 ft
>}«
Til
C o n e l u s o d e l método d e l o s n o d o s , d e t e r m i n e l a f u e r z a e n c a d a u n o d e l o s e l e m e n tos de la a r m a d u r a mostrada.
SOLUCION
1 000 Ib
t
l2ft
>{«
C u e r p o libre: armadura completa.
Se dibuja u n diagrama de cuerpo libre
d e t o d a l a a r m a d u r a . L a s f u e r z a s q u e actúan e n e s t e c u e r p o l i b r e c o n s i s t e n e n l a s
cargas a p l i c a d a s y e n las r e a c c i o n e s e n C y e n E . S e e s c r i b e n las e c u a c i o n e s d e e q u i librio siguientes:
1 2 ft
P
+"®M
C
= 0:
( 2 0 0 0 l b ) ( 2 4 f t ) + ( 1 0 0 0 l b ) ( 1 2 f t ) - £(6 f t ) = 0
£ = + 1 0 000 Ib
E = 1 0000 Ib f
-±>2F = 0 :
+ T S F = 0 :
I
1/
2 000 Ib
Í
C
-2 000 Ib - 1 000 Ib + 10 000 Ib + C. = 0
C
Y
*
3
X
F,„
5
N
= - 7 0001b
C
A D
2 000 Ib
F
A
F
B
A D
F
F
Ib
<
D
= 2 500 Ib C
<
C u e r p o libre: nodo D. C o m o l a f u e r z a e j e r c i d a p o r e l e l e m e n t o AD y a s e
determinó, a h o r a sólo s e t i e n e n d o s incógnitas i n v o l u c r a d a s c o n e s t e n o d o . D e n u e v o
s e u s a u n triángulo d e f u e r z a s p a r a d e t e r m i n a r l a s f u e r z a s d e s c o n o c i d a s e n l o s e l e m e n t o s DB y DE:
V
=
DB
FDE
162
A
1 500 Ib T
=
W
2500
= 7 000 Ib |
C u e r p o libre: nodo A. E l n o d o está s u j e t o a d o s f u e r z a s d e s c o n o c i d a s , e s t o
e s , a l a s f u e r z a s e j e r c i d a s p o r l o s e l e m e n t o s AB y AD. S e u s a u n triángulo d e f u e r z a s
p a r a d e t e r m i n a r F y F . S e o b s e r v a q u e e l e l e m e n t o AB j a l a a l n o d o y , p o r t a n t o ,
d i c h o e l e m e n t o está e n tensión. Además, e l e l e m e n t o AD e m p u j a e l n o d o y , p o r
t a n t o , d i c h o e l e m e n t o está e n compresión. L a s m a g n i t u d e s d e l a s d o s f u e r z a s s e o b t i e n e n a p a r t i r d e l a proporción
A B
2 0 0 0 Ib
= 0
F
F
DA
=
2(-g-)F
D A
F
D
E
D
B
=
2 5 0 0 Ib
= 3 000 Ib C
4
<*
C u e r p o libre: nodo B. C o m o e n e s t e n o d o actúan más d e t r e s f u e r z a s , s e
d e t e r m i n a n las d o s f u e r z a s d e s c o n o c i d a s F
y F
a l r e s o l v e r las e c u a c i o n e s d e
e q u i l i b r i o 1,F = 0 y 2 F ^ = 0 . D e m a n e r a a r b i t r a r i a s e s u p o n e q u e a m b a s f u e r z a s
d e s c o n o c i d a s actúan h a c i a f u e r a d e l n o d o , e s t o e s , q u e l o s e l e m e n t o s están e n t e n sión. E l v a l o r p o s i t i v o o b t e n i d o p a r a F , i n d i c a q u e l a suposición h e c h a f u e c o r r e c t a ;
p o r t a n t o , e l e l e m e n t o BC está e n tensión. E l v a l o r n e g a t i v o d e F . i n d i c a q u e l a
suposición h e c h a f u e i n c o r r e c t a ; p o r t a n t o , e l e l e m e n t o BE está e n compresión.
B
r
B
Í
x
B f
b¡
+ t ZF
y
= 0:
- 1 000 - -f(2 500) F
BF
ASF
= 0:
i
-íf-Fgj = 0
= - 3 750 Ib
F
BE
= 3 750 Ib C
<
= 5 250 Ib T
4
- 1 5 0 0 - - f - ( 2 5 0 0 ) - -§-(3 7 5 0 ) = 0
F
BC
F
BC
= + 5 250 Ib
F
B C
C u e r p o libre: nodo E.
S esupone que la fuerza desconocida F
f u e r a d e l n o d o . S i s e s u m a n l a s c o m p o n e n t e s x, s e e s c r i b e
= 0:
-*&F
Z
fF
FC
£
C
actúa h a c i a
+ 3 0 0 0 + -f (3 7 5 0 ) = 0
F
EC
= - 8 750 Ib
F
[:c
= 8 750 Ib C
<
A l s u m a r l a s c o m p o n e n t e s y, s e o b t i e n e u n a comprobación d e l o s cálculos r e a lizados
+ t 2F
S
= 10 0 0 0 -
f(3
750) -
^-(8
750)
= 10 0 0 0 - 3*000 - 7 000 = 0
(queda comprobado)
C u e r p o libre: nodo C . C o n l o s v a l o r e s d e F
y F , calculados p r e v i a m e n te, s e p u e d e n d e t e r m i n a r las r e a c c i o n e s C y C c o n s i d e r a n d o e l e q u i l i b r i o d e este
n o d o . C o m o dichas reacciones y a se d e t e r m i n a r o n a p a r t i r del e q u i l i b r i o de t o d a la
a r m a d u r a , s e obtendrán d o s v e r i f i c a c i o n e s d e l o s cálculos r e a l i z a d o s . También s e
p u e d e n u s a r l o s v a l o r e s c a l c u l a d o s d e t o d a s l a s f u e r z a s q u e actúan s o b r e e l n o d o
( f u e r z a s e n l o s e l e m e n t o s y r e a c c i o n e s ) y c o m p r o b a r q u e éste s e e n c u e n t r a e n e q u i librio:
C
B
C £
x
4*SF = - 5 250 + ^-(8 750) = - 5 250 + 5 250 = 0
(queda comprobado)
+ | 2F
(queda comprobado)
i
= - 7 0 0 0 + -f(8 750) = - 7 0 0 0 + 7 0 0 0 = 0
Desarrolle su competencia
3.1 a 3.8
Figura P3.6
Figura P3.7
U t i l i c e e l método d e l o s n o d o s p a r a d e t e r m i n a r l a f u e r z a e n c a d a
Figura P3.8
3.9
D e t e r m i n e la fuerza e n cada elemento d ela a r m a d u r a Pratt para techo
q u e s e m u e s t r a e n l a figura. E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n c o m presión.
164
9.6 k N
-| gg
Desarrolle su competencia
5.7 k N
[»—3.8 m
Figura P3.9
1.5 m 1.5 m 1.5 m
3.10
D e t e r m i n e la fuerza e n cada elemento d ela a r m a d u r a para ventilador
d e t e c h o q u e s e m u e s t r a e n l a figura. E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o
e n compresión.
3.11
D e t e r m i n e la fuerza e n cada e l e m e n t o de la a r m a d u r a H o w e para techo
q u e s e m u e s t r a e n l a figura. E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n c o m presión.
2kN
2kN
j
^
1.5 m 1.5 m 1.5 m
2kN
2kN
2kN
2 m
H
A
^
kN
C
Figura P3.10
600 Ib
600 Ib
300 I I
6 0 0 II
300 Ib
Figura P3.11
1
3.12
D e t e r m i n e l afuerza e ncada elemento d el aarmadura G a m b r e l para
t e c h o q u e s e m u e s t r a e n l a figura. E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n
compresión.
f — * \ ~ — 8 ft
t
F t g u r a
P
3
1 2
3.13
D e t e r m i n e la fuerza e n cada e l e m e n t o de la a r m a d u r a q u e se m u e s t r a
en la
figura.
12.5 k N
12.5 k N
12.5 k N
12.5 k N
compresión.
3.15
D e t e r m i n e l afuerza e ncada elemento d e l aa r m a d u r a W a r r e n para
p u e n t e q u e s e m u e s t r a e n l a figura. E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o
e n compresión.
Figura P3.Í4
6 f t
166
Análisis de estructuras
5.76 ft , 5.76 ft , 5.76 ft
5.76 ft
6 kips
6 kips
Figura P3.15
3.16
c a d a e n E.
R e t o m e el p r o b l e m a 3.15 y ahora suponga q u e se e l i m i n a la carga apli-
3.17
E n l a a r m a d u r a H o w e i n v e r t i d a p a r a t e c h o q u e s e m u e s t r a e n l a figura,
d e t e r m i n e l a f u e r z a e n e l e l e m e n t o DE y e n c a d a u n o d e l o s e l e m e n t o s l o c a l i z a d o s a l a
i z q u i e r d a d e DE. Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
6.72 ft
3.18
E n la armadura H o w e invertidapara techo que semuestra e n la
figura,
d e t e r m i n e la fuerza e n cada u n o de los elementos localizados a la derecha d e l elem e n t o DE. Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
Figura P 3 . 1 7 y P3.18
3.19
E n l a a r m a d u r a d e t i j e r a s p a r a t e c h o q u e s e m u e s t r a e n l a figura, d e t e r m i n e la fuerza e n cada u n o de los elementos localizados a la izquierda d e l e l e m e n t o
F G . Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
1 kN
3.20
E n l a a r m a d u r a d e t i j e r a s p a r a t e c h o q u e s e m u e s t r a e n l a figura, d e t e r m i n e la fuerza e n el e l e m e n t o F G y e n cada u n o de los elementos localizados a la der e c h a d e F G . Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
3.21
E n l a a r m a d u r a p a r a t e c h o d e e s t u d i o q u e s e m u e s t r a e n l a figura, d e t e r m i n e l a f u e r z a e n c a d a u n o d e l o s e l e m e n t o s l o c a l i z a d o s a l a i z q u i e r d a d e l a línea
FGH. Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
6 ft
2m
2m
2m
2m
2m
6 ft
6 ft
2m
Figura P3.19 y P3.20
Figura P3.21 y P3.22
i m. 1.6 m , 1.6 m , 1.6 m 1.6 m 1.6 m
!.4 m
3.22
E n l a a r m a d u r a p a r a t e c h o d e e s t u d i o q u e s e m u e s t r a e n l a figura, d e t e r m i n e l a fuerza e n el e l e m e n t o F G y e n cada u n o d e los elementos localizados a la der e c h a d e F G . Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
1.8 m
3.24
L a porción d e l a a r m a d u r a m o s t r a d a r e p r e s e n t a l a p a r t e s u p e r i o r d e
u n a t o r r e p a r a líneas d e transmisión d e energía eléctrica. P a r a l a s c a r g a s m o s t r a d a s ,
d e t e r m i n e l a f u e r z a e n c a d a u n o d e l o s e l e m e n t o s l o c a l i z a d o s p o r e n c i m a d e HJ.
Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
3.25
P a r a l a t o r r e y las cargas d e l p r o b l e m a 3 . 2 4 , a h o r a se sabe q u e F
= F
= 1.2 k N C y F
= 0 ; d e t e r m i n e l a f u e r z a e n e l e l e m e n t o HJ y e n c a d a u n o d e l o s
e l e m e n t o s l o c a l i z a d o s e n t r e HJ y NO. Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n
tensión o e n compresión.
CH
EH
r
' 6 ft ' 6 f t
3.23
E n l a a r m a d u r a a b o v e d a d a p a r a t e c h o q u e s e m u e s t r a e n l a figura, d e t e r m i n e la fuerza e n cada u n o de los elementos q u e conectan los nodos del A al F .
Además, e s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
1.2 k N
Figura P3.23
6ft
EJ
-2.21 m -
1.60 m
-2.21
m—H
Desarrolle su competencia
0.60 m
0.60 m
1.20 m
0.60 m
0.60 m
1.20 m
0.60 m
0.60 m
1.2 kN
Figura P3.24
3.26
R e t o m e e l p r o b l e m a 3.24 y a h o r a s u p o n g a q u e los cables q u e cuelgan
del lado derecho de la torre secaen al suelo.
en la
3.27
figura.
D e t e r m i n e la f u e r z a e n cada e l e m e n t o de la a r m a d u r a q u e se m u e s t r a
E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
en la
3.28
figura.
D e t e r m i n e la f u e r z a e n cada e l e m e n t o de la a r m a d u r a q u e se m u e s t r a
E s t a b l e z c a s i l o s e l e m e n t o s están e n tensión o e n compresión.
5ft
Figura P3.27
4.5 m
Figura P3.28
3.29. D e t e r m i n e s i l a s a r m a d u r a s d e l o s p r o b l e m a s 3 . 3 1 a ) , 3 . 3 2 a ) y 3 . 3 3 a ) s o n
armaduras simples.
3.30
D e t e r m i n e s i l a s a r m a d u r a s d e l o s p r o b l e m a s 3 . 3 1 & ) , 3.32¿>) y 3.33¿>)
son armaduras simples.
3.31
P a r a las cargas dadas, d e t e r m i n e los e l e m e n t o s d e f u e r z a c e r o e n c a d a
u n a d e las d o s a r m a d u r a s q u e s e m u e s t r a n e n l a
figura.
3.32
P a r a las cargas dadas, d e t e r m i n e los e l e m e n t o s d e f u e r z a c e r o e n c a d a
u n a d e las d o s a r m a d u r a s q u e s e m u e s t r a n e n l a
figura.
«Si | |
k
Figura P3.32
l
m
n
b)
Figura P3.31
-J gy
3.33
P a r a las cargas dadas, d e t e r m i n e los e l e m e n t o s d e f u e r z a c e r o e n c a d a
u n a d e las d o s a r m a d u r a s q u e se m u e s t r a n e n la
figura.
Figura P 3 . 3 3
3 . 3 4 D e t e r m i n e l o s e l e m e n t o s d e f u e r z a c e r o e n l a a r m a d u r a : a) d e l p r o b l e m a
3 . 2 3 , y b) d e l p r o b l e m a 3 . 2 8 .
3.6. ANÁLISIS DE ARMADURAS POR EL MÉTODO
DE SECCIONES
E l m é t o d o d e l o s n o d o s e s e l más e f i c i e n t e c u a n d o s e d e b e n d e t e r m i n a r l a s
f u e r z a s e n t o d o s l o s e l e m e n t o s d e u n a a r m a d u r a . S i n e m b a r g o , s i sólo s e
d e s e a e n c o n t r a r l a f u e r z a e n u n e l e m e n t o o e n u n número m u y r e d u c i d o d e
e l e m e n t o s , e l m é t o d o d e s e c c i o n e s e s e l más e f i c i e n t e .
S u p o n g a q u e s e d e s e a d e t e r m i n a r l a f u e r z a e n e l e l e m e n t o BD d e l a
a r m a d u r a q u e s e m u e s t r a e n l a figura 3 . 1 6 a ) . P a r a l l e v a r a c a b o e s t a t a r e a , s e
d e b e d e t e r m i n a r l a f u e r z a c o n l a c u a l e l e l e m e n t o BD actúa s o b r e e l n o d o B
o s o b r e e l n o d o D . S i s e u t i l i z a r a e l m é t o d o d e l o s n o d o s , s e seleccionaría e l
n o d o B o e l n o d o D c o m o e l c u e r p o l i b r e . S i n e m b a r g o , también s e s e l e c c i o n a c o m o c u e r p o l i b r e u n a porción más g r a n d e d e l a a r m a d u r a , c o m p u e s t a
p o r varios n o d o s y e l e m e n t o s , s i e m p r e y c u a n d o l af u e r z a deseada sea u n a
d e l a s f u e r z a s e x t e r n a s q u e actúan s o b r e d i c h a porción. Además, s i s e s e l e c c i o n a l a porción d e l a a r m a d u r a d e m a n e r a q u e s o l a m e n t e s e t e n g a u n t o t a l
d e t r e s f u e r z a s d e s c o n o c i d a s q u e actúan s o b r e l a m i s m a , l a f u e r z a d e s e a d a
s e p u e d e o b t e n e r a l r e s o l v e r l a s e c u a c i o n e s d e e q u i l i b r i o p a r a l a porción d e
l a a r m a d u r a e n cuestión. E n l a práctica, l a porción d e l a a r m a d u r a q u e d e b e
u t i l i z a r s e s e o b t i e n e al pasar una sección a través d e t r e s e l e m e n t o s d e l a a r m a d u r a , d elos c u a l e s u n o d e b e ser e l e l e m e n t o d e s e a d o , e s t o es, d i c h a p o r ción s e o b t i e n e a l d i b u j a r u n a línea q u e d i v i d a a l a a r m a d u r a e n d o s p a r t e s
c o m p l e t a m e n t e s e p a r a d a s p e r o q u e n o i n t e r s e q u e a más d e t r e s e l e m e n t o s .
C u a l q u i e r a d e l a s d o s p o r c i o n e s d e l a a r m a d u r a q u e s e o b t e n g a después d e
q u e los e l e m e n t o s intersecados h a n sido r e m o v i d o s p u e d e utilizarse c o m o
el cuerpo libre.'
E n l a figura 3 . 1 6 a ) s e h a p a s a d o l a sección nn a través d e l o s e l e m e n t o s
BD, BE y CE y s e h a s e l e c c i o n a d o l a porción ABC d e l a a r m a d u r a c o m o e l
c u e r p o l i b r e [ f i g u r a 3 . 1 6 f e ) ] . L a s f u e r z a s q u e actúan s o b r e e l d i a g r a m a d e
c u e r p o l i b r e s o n l a s c a r g a s P y P q u e están a p l i c a d a s e n l o s p u n t o s A y B y
las tres f u e r z a s desconocidas F , F
y F . C o m o n o s e s a b e si los e l e m e n t o s r e m o v i d o s e s t a b a n e n tensión o c o m p r e s i ó n , d e m a n e r a a r b i t r a r i a s e d i b u j a r o n las tres f u e r z a s y s e a l e j a r o n d e l c u e r p o l i b r e c o m o s ilos e l e m e n t o s
e s t u v i e r a n e n tensión.
2
¡
B D
g £
c £
' E n e l análisis d e c i e r t a s a r m a d u r a s , s e p a s a n s e c c i o n e s q u e i n t e r s e c a n a más d e t r e s e l e m e n t o s :
e n t o n c e s se p u e d e n d e t e r m i n a r las f u e r z a s e n u n o , o p o s i b l e m e n t e e n d o s , d e l o s e l e m e n t o s i n t e r s e c a d o s s i s e p u e d e n e n c o n t r a r e c u a c i o n e s d e e q u i l i b r i o q u e i n v o l u c r e n únicamente a u n a incógnita
(véanse l o s p r o b l e m a s 3 . 5 3 a 3 . 5 6 ) .
E l h e c h o d e q u e e l c u e r p o rígido ABC está e n e q u i l i b r i o s e p u e d e e x p r e s a r c o n t r e s e c u a c i o n e s , las cuales p u e d e n r e s o l v e r s e p a r a e n c o n t r a r t r e s
f u e r z a s d e s c o n o c i d a s . S i sólo s e d e s e a d e t e r m i n a r l a f u e r z a F , sólo s e n e c e s i t a e s c r i b i r u n a e c u a c i ó n , s i e m p r e y c u a n d o d i c h a ecuación n o c o n t e n g a a
l a s o t r a s incógnitas. P o r t a n t o , l a ecuación 2 M = 0 p r o p o r c i o n a e l v a l o r d e
la m a g n i t u d F
d ela fuerza F
[ f i g u r a 3.15¿)]. U n s i g n o p o s i t i v o e n e l r e s u l t a d o indicará q u e l a suposición o r i g i n a l e n relación c o n e l s e n t i d o d e F
f u e c o r r e c t a y q u e e l e l e m e n t o BD está e n tensión; u n s i g n o n e g a t i v o i n d i cará q u e l a suposición o r i g i n a l f u e i n c o r r e c t a y q u e BD está e n compresión.
B D
£
Bn
BD
B
D
P o r o t r a p a r t e , s i sólo s e d e s e a e n c o n t r a r l a f u e r z a F , s e d e b e e s c r i b i r
u n a ecuación q u e n o i n v o l u c r e a F
o a F ; e n e s t e c a s o , l a ecuación a p r o piada es2 M
= 0 . U n signo positivo para l am a g n i t u d F
d e l af u e r z a d e s e a d a m u e s t r a q u e l a suposición h e c h a f u e c o r r e c t a , e s t o e s , q u e e l e l e m e n t o
está e n tensión y u n s i g n o n e g a t i v o i n d i c a q u e l a suposición f u e i n c o r r e c t a ,
e s t o e s , q u e e l e l e m e n t o está e n compresión.
S i sólo s e d e s e a e n c o n t r a r l a f u e r z a F , l a ecuación a p r o p i a d a e s 1.F = 0 .
D e n u e v o , a p a r t i r d e l s i g n o d e l r e s u l t a d o s e d e t e r m i n a s i e l e l e m e n t o está
e n tensión o e n compresión.
C u a n d o s e d e t e r m i n a únicamente l a f u e r z a d e u n s o l o e l e m e n t o , n o s e
t i e n e d i s p o n i b l e u n a f o r m a i n d e p e n d i e n t e d e c o m p r o b a r l o s cálculos r e a l i zados. S i n e m b a r g o , c u a n d o s eh a n d e t e r m i n a d o t o d a s las f u e r z a s d e s c o n o c i d a s q u e actúan s o b r e e l c u e r p o l i b r e , s e p u e d e n v e r i f i c a r l o s cálculos s i s e
e s c r i b e u n a ecuación a d i c i o n a l . P o r e j e m p l o , s i F , F
yF
sedetermin a n d e l a m a n e r a señalada e n l o s párrafos a n t e r i o r e s , l o s cálculos p u e d e n
c o m p r o b a r s e a l v e r i f i c a r q u e 1iF = 0 .
C £
g
D
B £
B
CE
B £
y
B D
B
£
C
£
x
3.7. ARMADURAS FORMADAS POR VARIAS
ARMADURAS SIMPLES
C o n s i d e r e d o s a r m a d u r a s s i m p l e s ABC y DEF. S i e s t a s a r m a d u r a s están c o n e c t a d a s p o r t r e s b a r r a s BD, BE y CE, c o m o s e m u e s t r a e n l a figura 3 . 1 6 a ) ,
e n t o n c e s formarán e n c o n j u n t o u n a a r m a d u r a rígida ABDF.
Las armaduras
ABC
y DEF t a m b i é n s e p u e d e n c o m b i n a r e n u n a s o l a a r m a d u r a rígida s i s e
u n e n l o s n o d o s B y D e n u n s o l o n o d o B y s i s e c o n e c t a n l o s n o d o s CyE
por
m e d i o d e u n a b a r r a CE [ f i g u r a 3 . 1 6 f c ) ] . L a a r m a d u r a q u e s e o b t i e n e d e e s t a
f o r m a s e c o n o c e c o m o armadura
Fink. S e d e b e señalar q u e l a s a r m a d u r a s
d e l a figura 3 . 1 6 a ) y b) no s o n a r m a d u r a s s i m p l e s ; éstas n o s e p u e d e n c o n s t r u i r a p a r t i r d eu n a a r m a d u r a t r i a n g u l a r a la q u e s eagregan s u c e s i v a m e n t e
p a r e s d e e l e m e n t o s e n l a f o r m a d e s c r i t a e n l a sección 3 . 3 . S i n e m b a r g o , e s t a s
a r m a d u r a s s o n rígidas, c o m o s e v e r i f i c a a l c o m p a r a r l o s s i s t e m a s d e c o n e x i o n e s e m p l e a d o s p a r a m a n t e n e r j u n t a s l a s a r m a d u r a s s i m p l e s ABC y DEF
( t r e s b a r r a s e n l a figura 3 . 1 6 a ) y u n p e r n o y u n a b a r r a e n l a figura 3 . 1 6 ¿ )
c o n los sistemas d ea p o y o s p r e s e n t a d o s e n las secciones 2.24 y 2.25. L a s arm a d u r a s q u e están h e c h a s a p a r t i r d e v a r i a s a r m a d u r a s s i m p l e s c o n e c t a d a s
rígidamente s e c o n o c e n c o m o armaduras
compuestas.
E n u n a a r m a d u r a c o m p u e s t a , e l número d e e l e m e n t o s m y e l número
d e n o d o s n aún están r e l a c i o n a d o s p o r l a fórmula m = 2n — 3 . E s t o p u e d e
c o r r o b o r a r s e a l o b s e r v a r q u e , s i u n a a r m a d u r a c o m p u e s t a está a p o y a d a p o r
u n p e r n o s i n fricción y u n r o d i l l o ( i n v o l u c r a n d o así t r e s r e a c c i o n e s d e s c o n o c i d a s ) , e l n ú m e r o t o t a l d e incógnitas e s m + 3 y d i c h o n ú m e r o d e b e s e r i g u a l
a l número 2 n d e e c u a c i o n e s q u e s e o b t i e n e n a l e x p r e s a r q u e l o s n p e r n o s
están e n e q u i l i b r i o ; p o r t a n t o , s e c o n c l u y e q u e m = 2 n — 3 . L a s a r m a d u r a s
c o m p u e s t a s q u e están a p o y a d a s p o r u n p e r n o y u n r o d i l l o , o p o r u n s i s t e m a
e q u i v a l e n t e d e a p o y o s , s o n estáticamente
determinadas,
rígidas y completamente restringidas.
E s t o s e r e f i e r e a q u e todas las r e a c c i o n e s d e s c o n o c i das y las f u e r z a s e n t o d o s los e l e m e n t o s p u e d e n d e t e r m i n a r s e m e d i a n t e los
m é t o d o s d e l a estática y q u e l a a r m a d u r a n o s e colapsará n i s e moverá. S i n
e m b a r g o , n ot o d a s las f u e r z a s e n los e l e m e n t o s s e p u e d e n d e t e r m i n a r p o r
e l método d e l o s n o d o s , a m e n o s q u e s e r e s u e l v a u n g r a n número d e e c u a c i o n e s simultáneas. P o r e j e m p l o , e n e l c a s o d e l a a r m a d u r a c o m p u e s t a d e l a
figura
3 . 1 6 a ) , e s m á s e f i c i e n t e p a s a r u n a sección a través d e l o s e l e m e n t o s
BD, BE y CE p a r a d e t e r m i n a r l a s f u e r z a s e n l o s m i s m o s .
A h o r a s u p o n g a q u e l a s a r m a d u r a s s i m p l e s ABC y DEF están c o n e c t a d a s p o r cuatro b a r r a s BD, BE, CD y CE ( f i g u r a 3 . 1 7 ) . A h o r a , e l n ú m e r o
d e e l e m e n t o s m e s m a y o r q u e 2 n — 3 ; p o r t a n t o , r e s u l t a u n a armadura
hiperestática
y s e d i c e q u e u n o d e l o s c u a t r o e l e m e n t o s BD, BE, CD o CE e s
redundante.
S i l a a r m a d u r a está a p o y a d a p o r u n p e r n o e n A y p o r u n r o d i l l o
e n F , e l n ú m e r o t o t a l d e incógnitas e s m + 3 . C o m o m > 2n — 3 , a h o r a e l
n ú m e r o m + 3 d e incógnitas e s m a y o r q u e e l n ú m e r o 2 n d e e c u a c i o n e s
i n d e p e n d i e n t e s q u e s e t i e n e n disponibles; e nconsecuencia, l a a r m a d u r a e s
estáticamente
indeterminada.
P o r último, supóngase q u e l a s d o s a r m a d u r a s s i m p l e s ABC y DEF e s tán u n i d a s p o r u n p e r n o , c o m o s e m u e s t r a e n l a figura 3 . 1 8 a ) . E l n ú m e r o
d e e l e m e n t o s m e s m e n o r q u e 2 n — 3 . S i l a a r m a d u r a está a p o y a d a p o r
u n p e r n o e n A y u n r o d i l l o e n F , e l n ú m e r o t o t a l d e incógnitas e s m + 3 .
C o m o m < 2n — 3 , a h o r a e l n ú m e r o m + 3 d e incógnitas e s m e n o r q u e e l
número 2 n d e e c u a c i o n e s d e e q u i l i b r i o q u e s e d e b e n c u m p l i r ; p o r t a n t o , l a
a r m a d u r a no es rígida y s e colapsará b a j o s u p r o p i o p e s o . S i n e m b a r g o , s i s e
u s a n d o s p e r n o s p a r a a p o y a r l a , l a a r m a d u r a s e v u e l v e rígida y n o s e colapsará
[ f i g u r a 3 . 1 8 f e ) ] . A h o r a s e o b s e r v a q u e e l n ú m e r o t o t a l d e incógnitas e s m +
4 y e s i g u a l a l n ú m e r o 2 n d e e c u a c i o n e s . E n términos más g e n e r a l e s , s i l a s
r e a c c i o n e s e n l o s a p o y o s i n v o l u c r a n r incógnitas, l a condición p a r a q u e u n a
a r m a d u r a c o m p u e s t a s e a e s t á t i c a m e n t e d e t e r m i n a d a , rígida y p o r c o m p l e t o
r e s t r i n g i d a e s m + r = 2 n . S i n e m b a r g o , a u n q u e e s t a condición e s n e c e saria, n oe s suficiente p a r a e l e q u i l i b r i o d e u n a e s t r u c t u r a q u e deja d e s e r
rígida c u a n d o s e s e p a r a d e s u s a p o y o s (véase sección 3 . 1 0 ) .
Figura 3.18
B
B
a)
b)
28 kips
2 8 kips
PROBLEMA RESUELTO 3.2
K
16 kips
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s EF y GI d e l a a r m a d u r a m o s t r a d a e n l a
8ft
28 kips
figura.
' 8 ft
28 kips
SOLUCION
\c
A
T
10 f t
J
B
E
/V
AY
•
F
B
i
H\
l
8ñ'
<
K
I
\G
i
8ft'' 8ft'
<
8ft'
16 k i p s
C u e r p o libre: armadura completa. S e d i b u j a u n d i a g r a m a d e c u e r p o l i b r e d e t o d a l a a r m a d u r a ; l a s f u e r z a s e x t e r n a s q u e actúan s o b r e e s t e c u e r p o l i b r e
c o n s i s t e n e n l a s c a r g a s a p l i c a d a s y l a s r e a c c i o n e s e n B y J. S e e s c r i b e n l a s s i g u i e n t e s
ecuaciones de equilibrio:
+"¡2M = 0 :
B
- ( 2 8 kips)(8 ft) - (28 kips)(24 ft) - (16 kips)(10 ft) + /(32 ft) = 0
/ = + 3 3 kips
28 kips
2 8 kips
1
i
±»2F_ = 0 :
B
i
J = 3 3kips f
+ 16 kips = 0
m
B
x
= - 1 6 kips
B
X
= 16 kips*
"¡2M = 0 :
;
16 kips
( 2 8 k i p s ) ( 2 4 f t ) + ( 2 8 káps)(8 f t ) - ( 1 6 l d p s ) ( 1 0 f t ) - 5 ^ ( 3 2 f t ) = 0
B = + 2 3 kips
28 kips
l
F u e r z a en el elemento EF.
S e p a s a l a sección nn a través d e l a a r m a d u r a
d e m a n e r a q u e sólo i n t e r s e q u e a l e l e m e n t o EF y a o t r o s d o s e l e m e n t o s a d i c i o n a l e s .
Después d e q u e s e h a n r e m o v i d o l o s e l e m e n t o s i n t e r s e c a d o s , l a porción d e l l a d o
i z q u i e r d o d e l a a r m a d u r a s e s e l e c c i o n a c o m o e l c u e r p o l i b r e . S e o b s e r v a q u e están
i n v o l u c r a d a s t r e s incógnitas; p a r a e l i m i n a r l a s d o s f u e r z a s h o r i z o n t a l e s , s e e s c r i b e
+ 1 lF
= 0:
y
16 k i p s
í
+ 2 3 kips - 2 8kips - F
F
D
2o kips
B , = 2 3kips f
EF
E
F
= 0
= —5 kips
E l s e n t i d o d e F s e seleccionó a l s u p o n e r q u e e l e l e m e n t o EF está e n tensión; e l
s i g n o n e g a t i v o o b t e n i d o i n d i c a q u e e n r e a l i d a d e l e l e m e n t o está e n compresión.
£ F
F
FF
10 ft
= 5 kips C
4
F u e r z a en el elemento Gí. S e p a s a l a sección mm a través d e l a a r m a d u r a
d e m a n e r a q u e sólo i n t e r s e q u e a l e l e m e n t o GI y a o t r o s d o s e l e m e n t o s a d i c i o n a l e s .
Después d e q u e s e h a n r e m o v i d o l o s e l e m e n t o s i n t e r s e c a d o s , s e s e l e c c i o n a l a p o r ción d e l l a d o d e r e c h o d e l a a r m a d u r a c o m o e l c u e r p o l i b r e . O t r a v e z están i n v o l u c r a d a s t r e s f u e r z a s d e s c o n o c i d a s ; p a r a e l i m i n a r l a s d o s t u e r z a s q u e p a s a n a través d e l
p u n t o H se escribe
+"¡2M
H
= 0:
(33 kips)(8 ft) - (16 kips)(10 ft) + F ( 1 0 ft) = 0
C I
-10.4 kips
Fe,
10.4 kips C
^
171
1 kN
PROBLEMA RESUELTO 3.3
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s FH, GH y GI d e l a a r m a d u r a p a r a t e c h o m o s trada e n la
figura.
fc = 8r
5k-N 5 k N
5kN
6 paneles @ 5 m = 3 0 m-
SOLUCION
C u e r p o libre: armadura completa.
A partir del diagrama de cuerpo libre
p a r a t o d a l a a r m a d u r a s e e n c u e n t r a n l a s r e a c c i o n e s e n A y L:
A = 12.50 k N f
Se observa
que
tan a =
1 kN
c"X
= 5.33 m
1
8 m
15 m
a = 28.07°
0.5333
CI
'H
F
FG
GL
F u e r z a en el elemento G I . S e p a s a l a sección nn a través d e l a a r m a d u r a ,
c o m o s e m u e s t r a e n l a f i g u r a . C o n e l u s o d e l a porción HLI d e l a a r m a d u r a c o m o e l
cuerpo libre, se obtiene el valor de F al escribir
12.50 k N
í
L = 7.50 k N |
1 kN
+*¡2M = 0 :
H
7
(7.50 k N ) ( 1 0 m ) - (1 k N ) ( 5 m ) - F ( 5 . 3 3 m ) = 0
G Í
F
G¡
.j|gi¡il¡l§ijJ
= +13.13 k N
F
c¡
= 13.13 k N T
*
s»»^
j
•«—5 m — — - - 5 m — * - | . 5 0 k N
F u e r z a en el elemento F H . E l v a l o r d e F s e o b t i e n e a p a r t i r d e l a e c u a ción 2 M = 0 . S e m u e v e F a l o l a r g o d e s u línea d e acción h a s t a q u e actúe e n e l
p u n t o F , d o n d e s e d e s c o m p o n e e n s u s c o m p o n e n t e s x y y. A h o r a , e l m o m e n t o d e F
c o n r e s p e c t o a l p u n t o G e s i g u a l a (F e o s a)(8 m ) .
FH
C
F H
y H
F f « eos a
Fp
H
sen a
FH
+1SM
= 0:
( 7 . 5 0 k N ) ( 1 5 m ) - ( 1 k N ) ( 1 0 m ) - ( 1 k N ) ( 5 m ) + (F
1 kN
FH
a=
-5 m » « 5 m -
G
-13.81 k N
28.07°
-«—5 m — ^ |
F u e r z a en el elemento G H .
.50 k N
GI
HI
tan/3
1 kN
F
FH
P r i m e r o se observa
5 m
1(8
m)
eos a ) ( 8 m ) = 0
= 13.81 k N C
-i
que
0 . 9 3 7 5 8 = 43.15°
Entonces, e l valor d e F
se d e t e r m i n a a l d e s c o m p o n e r l a fuerza F
c o m p o n e n t e s x y y e n e l p u n t o G y a l r e s o l v e r l a ecuación 2 M = 0 .
GH
G H
e n sus
L
tf cft
tfGH
e
o
s
P
seu
4
+ )SM
R
50 k N
L
= 0:
( 1 k N ) ( 1 0 m ) + ( 1 k N ) ( 5 m ) + (F
CH
F
GH
= -1.371 k N
e o s B)(15 m ) = 0
F
CII
= 1.371 k N C
4
Desarrolle su competencia
6.25 ft
3.35
U n a a r m a d u r a W a r r e n para puentes se carga e n la f o r m a que
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s CE, DE y DF.
muestra
la
3.36
U n a a r m a d u r a W a r r e n para puentes se carga e n la f o r m a que
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s EG, FG y FH.
muestra
la
3.37
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s BD y DE d e l a a r m a d u r a q u e s e
muestra e n la
figura.
135 k N
12.5 f t
12.5 f t . 12.5 f t . 12.5 f t
12.5 f t
12.5 ft
12.5 ft 12.5 ft
6 0 0 0 Ib 6 0 0 0 Ib
Figura P3.35 y P3.36
A
Figura P3.37 y P3.38
3.38
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s DG y EG d e l a a r m a d u r a q u e s e
muestra e n la
figura.
3.39
U n a a r m a d u r a para piso se carga e n l a f o r m a que muestra l a
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s CF, EF y EG.
¡kN
4kN
4k.N
lo.8
m iq.8
m
T
DT
IT
3kN
2kN
2 kN
figura.
1 kN
10.8 m 10.8 m 10.8 m 10.i,8 m i
c;f
fjf
J l
Figura P3.39 y P3.40
3.40
U n a a r m a d u r a para piso se carga e n l a f o r m a que muestra l a
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s FI, HI y HJ.
figura.
3.41
U n a a r m a d u r a de tiro plano para techo secarga e n la f o r m a que muest r a l a figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s CE, DE y DF.
3.42
U n a a r m a d u r a de tiro plano para techo se carga e n la f o r m a que m u e s t r a l a figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s EG, GH y HJ.
3.43
muestra la
U n a armadura H o w e tipo tijera para techo se carga e nl af o r m a que
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s DF, DG y EG.
3.44
m u e s t r a la
U n a armadura H o w e tipo tijera para techo se carga e nl af o r m a que
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s GI, HI y HJ.
2.4 m
2.4 m
Figura P3.41 y P3.42
173
8ft
8ft
8ft
8 ft
8ft
Figura P3.43 y P3.44
1.5 kN
3 m
3 m
3m
3 m
3m
3 m
figura.
3.45
U n a a r m a d u r a P r a t t para techo se carga e n l a f o r m a que m u e s t r a l a
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s CD, DE y DF.
figura.
3.46
U n a a r m a d u r a P r a t t para techo se carga e n l a f o r m a que m u e s t r a l a
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s FH, FI y GI.
3.47
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s AD, CD y CE d e l a a r m a d u r a q u e
se m u e s t r a e n l a
figura.
Figura P3.45 y P3.46
-4.5 m -
•—4.5 m -
-4.5 m 20 k N
20 k N
36 k N
>G
0.9 k
! 2.4 m
o-
o
F
E
H
Figura P3.47 y P3.48
1 4 f t -*\
31.5 ft
s e
3.48
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s DG, FG y FH d e l a a r m a d u r a q u e
muestra e n la
figura.
la
3.49
U n a a r m a d u r a para techo de estadio se carga en la f o r m a que muestra
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s AB, AG y FG.
la
3.50
U n a a r m a d u r a para techo de estadio se carga e n la f o r m a que muestra
figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s AE, EF y FJ.
3.51
U n a a r m a d u r a polinesia, o de dos tiros, para techo se carga e n la f o r m a
q u e m u e s t r a l a figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s DF, EF y EG.
Figura P3.49 y P3.50
6ft
6 ft
6ft
6ft
6 ft
, 6 ft
6 ft
6ft
350 Ib
400 Ib
4 0 0 Ib
300 Ib
300 I b ,
tlb
200 I
4 ft
4.5 ft
Ése
3 m
3ra
C
E
' ' 9.6 ft '
8.4 f t
3
j
t
iaiBiiBxStSimi
G
;
L
6 ft
6 ft
8 . 4 ft
3 m 3 m
' 9 . 6 ft
Figura P3.57 y P3.52
3.52
U n a a r m a d u r a polinesia, o de dos tiros, para techo se carga e n la f o r m a
q u e m u e s t r a l a figura. D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s HI, GI y GJ.
3.53
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s AF y EJ d e l a a r m a d u r a q u e s e
m u e s t r a e n l a figura, c u a n d o P , = Q = 1 . 2 k N . (Sugerencia: U s e l a sección aa.)
Figura P3.53 y P3.54
3.54
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s AF y EJ d e l a a r m a d u r a q u e s e
m u e s t r a e n l a figura, c u a n d o P = 1 . 2 k N y Q = 0 . (Sugerencia: U s e l a sección aa.)
Desarrolle su competencia
3.55
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s EH y GI d e l a a r m a d u r a q u e s e
m u e s t r a e n l a figura. (Sugerencia: U s e l a sección aa.)
1 5 ft *
1 5 ft 4 1 5 ft é
12 k i p s
1 2 kips
-| ~JC
1 5 ft
12 kips
Figura P3.55 y P3.56
3.56
D e t e r m i n e l a f u e r z a e n l o s e l e m e n t o s HJ e IL d e l a a r m a d u r a q u e s e
m u e s t r a e n l a figura. (Sugerencia: U s e l a sección hb.)
3.57 y 3.58
L o s e l e m e n t o s diagonales e n los paneles centrales de la t o r r e de
transmisión q u e s e m u e s t r a e n l a figura s o n m u y d e l g a d o s y sólo p u e d e n a c t u a r e n
tensión; a t a l e s e l e m e n t o s s e l e s c o n o c e c o m o contravientos. P a r a l a s c a r g a s d a d a s ,
d e t e r m i n e : a) cuál d e l o s d o s c o n t r a v i e n t o s m e n c i o n a d o s actúa, y b) l a f u e r z a e n e s e
contraviento.
3.57
C o n t r a v i e n t o s CJ y HE.
3.58
C o n t r a v i e n t o s IO y KN.
0.60 m
0.60 m
1.20 m
0.60 m
0.60 m
1.20 m
0.60 m
0.60 m
4.8 kips
4.8 kips
4.8 kips
U- i if t — | — u
f t
"^
1 1
2.4 kips
-^*~
ft
11
2.4 kips
~~\
ñ
9 . 6 ft
^>s>.
F\
Figura P3.57 y P3.58
a:s.."
Figura P3.59
3.59 y 3.60
L o s e l e m e n t o s d i a g o n a l e s e n l o s p a n e l e s c e n t r a l e s d e l a s a r m a - 4 . 8 k i p s¡ 44.»
. 8 kk ii pp ss
44.»
. 8 kK ii pp ss
2B .. 44 kK ii pp ss
d u r a s q u e s e m u e s t r a n e n l a s figuras s o n m u y d e l g a d o s y sólo p u e d e n a c t u a r e n
1 1 tt —|— 1 1 ft^*|" 1 1 ft"*J^** " "
tensión; a t a l e s e l e m e n t o s s e l e s c o n o c e c o m o contravientos. D e t e r m i n e l a s f u e r z a s
e n l o s c o n t r a v i e n t o s q u e actúan b a j o l a s c a r g a s d a d a s .
A
3.61
C l a s i f i q u e c a d a u n a d e l a s e s t r u c t u r a s m o s t r a d a s e n l a figura c o m o c o m p l e t a , p a r c i a l o i m p r o p i a m e n t e r e s t r i n g i d a ; s i l a e s t r u c t u r a está c o m p l e t a m e n t e r e s t r i n g i d a , clasifíquela c o m o estáticamente d e t e r m i n a d a o i n d e t e r m i n a d a . ( T o d o s l o s
e l e m e n t o s p u e d e n a c t u a r t a n t o e n tensión c o m o e n compresión.)
>
I
Figura P3.60
2J£.4
. 4 kKi p s
" i
9 . 6 ft
•J yg
Análisis de estructuras
3.62 a 3.66
C l a s i f i q u e c a d a u n a d e las e s t r u c t u r a s m o s t r a d a s e n las
figuras
c o m o c o m p l e t a , p a r c i a l o i m p r o p i a m e n t e r e s t r i n g i d a ; s i l a e s t r u c t u r a está c o m p l e t a m e n t e r e s t r i n g i d a , clasifíquela c o m o estáticamente d e t e r m i n a d a o i n d e t e r m i n a d a .
( T o d o s l o s e l e m e n t o s p u e d e n a c t u a r t a n t o e n tensión c o m o e n compresión.)
r
r
a)
Figura P3.66
r
r
b)
r
r
c)