CUANTILES

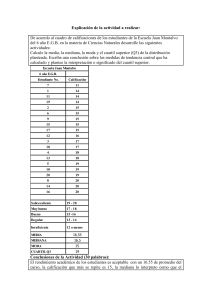
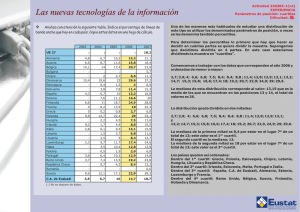
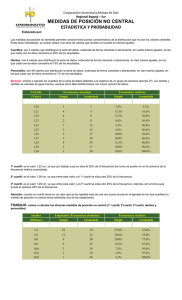
NM4: CUANTILES
Constituyen una generalización del concepto de
mediana. Así como la mediana divide a la serie
estudiada en dos partes con el mismo número de
elementos cada una, si la división se hace en cuatro
partes, o en diez partes, o en cien partes, llegamos
al concepto de cuantil.
Hay, principalmente, tres cuantiles importantes:
cuartiles, deciles y percentiles.
CUARTILES
Son tres valores con las siguientes características:
Q1: Primer cuartil, que es el valor de la variable por
debajo del cual queda 1/4 de los elementos de la
serie estudiada.
Q3: Tercer cuartil, que es el valor de la variable por
debajo del cual quedan los 3/4 de los elementos
que constituyen la serie.
Evidentemente el segundo cuartil coincide con la
mediana. Como puede comprobarse, no tendría
ninguna utilidad definir el cuarto cuartil. El cálculo
de los cuartiles se realiza por el mismo
procedimiento que el cálculo de la mediana, pues
hay únicamente una diferencia cuantitativa entre
ambas medidas, pero tienen significados paralelos.
Así, el primer cuartil se hallará aplicando la
siguiente fórmula:
Q1  l 
D1, el decil 1, deja el 10% de los valores de la serie
por debajo de él.
Análogamente ocurre con los deciles D2,
D3,.......D9. El decil 8, por ejemplo, deja el 80% de
la masa de datos investigada por debajo de él.
Las fórmulas para calcularlos son también análogas
a las de la mediana.
Por ejemplo:
I N
D1  l  (  f i )
f 10
D9  l 
I 3N
(
 fi )
f 4
donde:
l: límite inferior de la clase a la que pertenece el
cuartil, que es la clase que deja por debajo de ella
el 25% de las observaciones (o el 75% en el caso
de Q3)
I: amplitud del intervalo.
f: frecuencia de la clase cuartílica.
N: total de elementos de la muestra.
fi: frecuencia acumulada de todos los valores
inferiores a la clase que contiene el cuartil.
I 9N
(
 fi )
f 10
PERCENTILES
Hay 99 percentiles que se denotan: P 1, P2,
P3,.......,P98, P99. Así P90, por ejemplo, deja por
debajo de él el 90% de los elementos.
La fórmula para realizar el cálculo del percentil 45,
por ejemplo sería:
I N
(  fi )
f 4
y el tercer cuartil:
Q3  l 
DECILES
Es la segunda clase de cuantiles. Si se divide toda
la serie en diez partes iguales tendremos los
deciles.
P45  l 
I 45N
(
 fi )
f 100
Ejercicio: De la siguiente serie hallar el primero y
el tercer cuartil, el segundo y el séptimo decil y los
percentiles 8 y 73.
Resp: Q1 = 34,82; Q3 = 47,36; D2 = 32,85; D7 =
45,83; P8 = 26,94; P73 = 46,75.
Obsérvese que entre los 6 cuantiles calculados,
aparecen valores muy parecidos. En particular se
dan las siguientes coincidencias:



El segundo cuartil equivale a la mediana
El quinto decil y el quincuagésimo percentil se
corresponden también con la mediana.
Los percentiles P25 y P75 se corresponden con
el primer y tercer cuartil, respectivamente.