Ejercicios_de_riesgo_y_rentabilidad
Anuncio
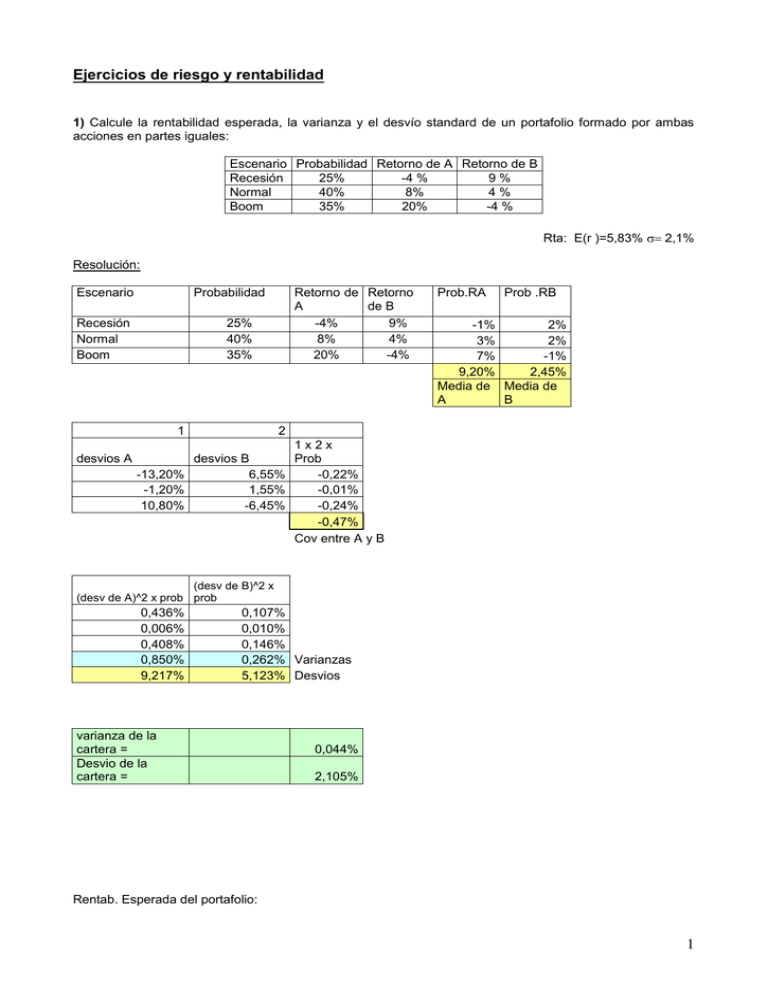
Ejercicios de riesgo y rentabilidad 1) Calcule la rentabilidad esperada, la varianza y el desvío standard de un portafolio formado por ambas acciones en partes iguales: Escenario Probabilidad Retorno de A Retorno de B Recesión 25% -4 % 9% Normal 40% 8% 4% Boom 35% 20% -4 % Rta: E(r )=5,83% 2,1% Resolución: Escenario Probabilidad Recesión Normal Boom 25% 40% 35% 1 desvios A Retorno de Retorno A de B -4% 9% 8% 4% 20% -4% Prob.RA Prob .RB -1% 2% 3% 2% 7% -1% 9,20% 2,45% Media de Media de A B 2 1x2x desvios B Prob -13,20% 6,55% -0,22% -1,20% 1,55% -0,01% 10,80% -6,45% -0,24% -0,47% Cov entre A y B (desv de B)^2 x (desv de A)^2 x prob prob 0,436% 0,006% 0,408% 0,850% 9,217% 0,107% 0,010% 0,146% 0,262% Varianzas 5,123% Desvios varianza de la cartera = Desvio de la cartera = 0,044% 2,105% Rentab. Esperada del portafolio: 1 E(r) = Varianza del portafolio= 0.092 0.0245 0.05825 2 0,85* 0,52 0,262* 0,52 2 * 0,5 * 0,5 * (0,47) 0,044% Desvio del portafolio = 2,105% 2) Un inversor posee un capital de $100.000 y está evaluando cómo invertirlo. Suponga que está considerando invertir en dos activos riesgosos, A y B, y un activo libre de riesgo, F. A continuación se proporciona la información sobre rentabilidades esperadas, riesgo y correlación: Acción A Acción B Bonos del Tesoro (F) Rendimiento Esperado 20% 15% 5% Desvío 30% 20% El coeficiente de correlación entre la rentabilidad de la acción A y la de la acción B es 0.25. Calcular: a) La rentabilidad esperada y el riesgo del portafolio si el inversor decide invertir $50.000 en el activo A y $50.000 en el activo B. Rta: 17,5 % y 20% E (rp ) 0.5 * 20% 0.5 *15% 17.5% p2 0.52 * 302 0.52 * 202 2 * 0.5 * 0.5 * 0.25* 30% * 20% 400 p 20% b) La rentabilidad esperada y el riesgo de un portafolio compuesto por $25.000 en el activo A y $75.000 en bonos del tesoro. Rta: 8,75% y 7,5% E (rp ) 0.25* 20% 0.75* 5% 8.75% p2 0.252 * 302 56.25 p 7.5% Aclaración: Como los bonos del tesoro tienen riesgo igual a 0, de la fórmula de la varianza se elimina el segundo y tercer término, se podría usar directamente: p 0,25* 30 7,5% c) La rentabilidad esperada y el riesgo de un portafolio compuesto por los tres activos en las siguientes proporciones: 35% en A, 25% en B y 40% en F. Rta: 12,75% y 12,71% 2 E (rp ) 0.35* 20% 0.25*15% 0.4 * 5% 12.75% p2 0.352 * 302 0.252 * 202 2 * 0.35* 0.25* 0.25* 30* 20 161.5 p 12.71% d) Conforme al CAPM, si conocemos que el beta del activo A es 1,05 ¿Cuál sería la rentabilidad esperada del portafolio de mercado y el beta de los otros dos activos, B y F? Rta: 19,28%; 0,7 y 0. E (rA ) r f A rm r f 20 5 1.05* (rm 5) rm 20 5 5 19.285% 1.05 El beta del activoB será : r r 15 5 B B f 0.7 rm r f 19.285 5 El beta del activoF es : F 0 e) ¿Cuál sería el costo del capital propio de la acción de una empresa C, conforme al CAPM, si tal acción tiene la misma volatilidad o desvío estándar que la de la empresa B? Respuesta: Para conocer el rendimiento esperado de la acción de la empresa C deberíamos conocer su Beta, información que no se nos brinda. Dos activos pueden tener la misma volatilidad o desvío estándar pero ello no significa que deban tener la misma rentabilidad esperada conforme al CAPM. El beta de un activo determina su rentabilidad esperada, pues este es la medida del riesgo relevante o remunerable de un activo (riesgo sistemático, de mercado o no diversificable). f) Si la correlación entre el activo A y el activo B fuera 1 ¿Cuál sería el desvío estándar de la cartera del punto a)? p2 0.5 2 * 302 0.5 2 * 202 2 * 0.5 * 0.5 *1* 30% * 20% 625 p 25% Rta: 25% g) Puede comprobar fácilmente que el desvío estándar de la rentabilidad del portafolio del punto anterior es un promedio ponderado del desvío de los activos que lo integran ¿Es este resultado siempre válido? Respuesta: p 0.5 * 30 0.5 * 20 25% La afirmación que el desvío estándar del portafolio es un promedio ponderado del desvío de los activos que lo integran es correcta en este caso que rho=1. Pero ese resultado no es válido para coeficientes de correlación distintos de 1. En el caso planteado, no hay efecto diversificación pues 3 los activos están perfectamente correlacionados. Para coeficientes de correlación diferentes de 1 el desvío del portafolio será menor al promedio del desvío de los activos (efecto diversificación.) h) Si los rendimientos del activo A y del activo B fueran independientes (coef. De correlación igual a 0) ¿Cuál sería el desvío del portafolio del punto anterior? Hay en este caso efecto diversificación? Rta:18,03% p2 0.5 2 * 302 0.5 2 * 202 2 * 0.5 * 0.5 * 0 * 30% * 20% 325 p 18.03% También hay efecto diversificación. 3) ¿Cuál es el rendimiento esperado del portafolio de mercado en un momento en que el rendimiento de las letras del Tesoro es de 5% y una acción con una beta de 1,25 tiene un rendimiento esperado de 14%? Rta: 12,2% 0.14 0.05 1.25 E (rM ) 0.05 E (rM ) 0.14 0.05 0.05 0.122 1.25 4) ¿Cuál es la tasa de retorno esperada por un inversor sobre una acción que tiene una beta de 0,9 cuando el rendimiento del mercado es del 15%, y las Letras del Tesoro rinden un 7%? Rta: 14,2% E(r ) 0.07 0.9 0.15 0.07 0.142 5) ¿Qué retorno podría esperar un inversor cuyo portafolio está compuesto en un 75% por el portafolio del mercado y en un 25% por Letras del tesoro, si la tasa libre de riesgo es del 5% y la prima de riesgo del mercado es de 9%? Rta:11,75% E (rM ) 0.09 0.05 0.14 E (r ) 0.75 0.14 0.25 0.05 0.1175 6) Una acción tiene a = 0,8 y E(ra) = 13% anual. La rentabilidad del activo libre de riesgo es 4% anual. 1. ¿Cuál será el rendimiento esperado de una cartera igualmente invertida en ambos activos? 8,5% Rta: E(rcart ) 0.5 0.13 0.5 0.04 0.085 2. Si el de una cartera formada por estos dos activos es 0,6 ¿cuál será el peso de cada activo? Rta: 0,75 del activo “a” y 0,25 del libre de riesgo. 4 cart xa 0.8 x f 0 xa 0.6 0.75 0.8 x f 1 xa 0.25 3. Si el rendimiento esperado de una cartera formada por estos dos activos es del 11%, ¿cuál es su ? Rta: = 0,6222 E (rmerc ) cart 0.13 0.04 0.04 0.1525 0.8 0.11 0.04 0.6222 0.1525 0.04 7) La rentabilidad de las letras del tesoro es del 4%, y la rentabilidad esperada de la cartera de mercado es de 12%. Basándose en el CAPM: 1. ¿Cuál es la prima de riesgo de mercado? Rta: 8% prima 0.12 0.04 0.08 2. Cuál es la rentabilidad deseada para una inversión con un beta de 1,5? Rta: 16% E (r ) 0.04 1.5 0.08 0.16 3. Si el mercado espera una rentabilidad de 11,2% de la acción X, ¿cuál es la beta de esta acción? Rta: 9% X 0.112 0.04 0.09 0.12 0.04 8) Determine la Beta de la acción A, basándose en la siguiente serie de rentabilidades: Retornos de la Acción A Retorno del Mercado 6% 5% 15% 12,5% - 4,2% - 3,5% 9% 7,5% Rta.: 1,20 COVARact merc 0.005367 1.2 VARmerc 0.004473 9) Determinar el costo de capital propio que exigirán los accionistas de una empresa que cotiza en bolsa cuyo beta es de 1,02. Usted dispone de la siguiente información referida a tasas libres de riesgo y al rendimiento esperado del mercado son: 5 PLAZO TASA 1 año 5 años 10 años 15 años 3,5% 5% 6,5% 8% RENDIMIENTO DEL MERCADO 10% 12% 15% 18% Si usted piensa mantener sus inversiones en esa compañía por 15 años. ¿Cuál será el rendimiento esperado de las mismas? Rta: 18,20% E (rm )15 años 0.18 r f 15 años 0.08 E (r ) 0.08 1.020.18 0.08 0.182 10) Suponga que usted hubiera invertido 30.000 dólares en las cuatro siguientes acciones. Título Cantidad Invertida Acciones A Acciones B Acciones C Acciones D $5.000 $10.000 $8.000 $7.000 Beta 0.75 1.10 1.36 1.88 La tasa libre de riesgo es de 4% y el rendimiento esperado de la cartera de mercado es de 15%. Basándose en el CAPM ¿cuál será el rendimiento esperado de la cartera?. ( El beta de la cartera es un promedio ponderado del beta de los activos que lo integran) Rta: 18,22% Entonces este beta será: (5000/30000)*0.75+(10000/30000)*1.10+(8000/30000)*1.36+(7000/30000)*1.88= 1,293 La rentabilidad esperada de la cartera será: 4 + 1,293 (15 – 4) = 18.22% Un procedimiento alternativo (más extenso) hubiera sido calcular las rentabilidades esperadas de cada uno de los 4 activos, a partir de su beta, y luego calcular la rentabilidad esperada del portafolio como un promedio ponderado de las rentabilidades esperadas de los activos individuales. 11)Dados los siguientes precios de fin de período de acciones correspondientes a la Cía. A, con las siguientes probabilidades y suponiendo un precio actual por acción de $50, Probabilidad Precio a fin de período por acción 0,15 $35 0,10 $42 0,30 $50 0,20 $55 0,25 $60 Calcular el retorno para cada probabilidad. ¿Cuál es el retorno esperado y la varianza del retorno? R: 0,9% y 16,73% 6 Rendimientos Por ej -0,30 -0,16 0,00 0,10 0,20 (35-50)/50 = - 0,30 12) Con los siguientes datos: Acción A B C D E Rentab. Esperada (en%) de la acción si la rentab. de mercado es -10% 0 -20 -30 +15 +10 Rentab. Esperada (en %) de la acción si la rentab. de mercado es +10% +20 +20 0 +15 -10 ¿Cuál es la beta de cada una de las acciones del cuadro? R: 1; 2; 1,5; 0 ; -1 Beta de A = (0-20)/(-10-10) = -20/-20 = 1 Beta de B = (-20-20)/(-10-10) = -40/-20 = 2 Beta de C = -30/-20 = 1,5 Beta de D = 0/-20 = 0 Beta de E = 20/-20 = -1 13) Teniendo en cuenta que Rf = 10%, Rm = 16% y el retorno sobre la acción C es 18%: a) Determinar la beta implícita para la acción. b) Cuál será el retorno de la acción si su beta es 0,75? R.: 1,33 y 14,5% 0,18 0,10 B.(0,16 0,10) B 1,33 b) Rc 0,10 0,75.(0,16 0,10) 14,5% a) 14) La Cía. de inversiones J maneja un fondo de acciones compuesto por 5 acciones con los siguientes valores de mercado y betas: Acción A B C D E total Valor de mercado ($) 100.000 50.000 75.000 125.000 150.000 500.000 Beta 1,10 1,20 0,75 0,80 1,40 Si Rf = 7% y Rm = 14% ¿Cuál es el retorno esperado del porfolio? 7 R: 14,50% Acción A B C D E total Valor de mercado ($) Beta 100.000 50.000 75.000 125.000 150.000 500.000 1,10 1,20 0,75 0,80 1,40 % de particip 0,20 0,10 0,15 0,25 0,30 Rf 0,07 0,07 0,07 0,07 0,07 Rto esperado del mercado 0,14 0,14 0,14 0,14 0,14 Rendim. 0,1470 0,1540 0,1225 0,1260 0,1680 * 0,07 + (0,14 - 0,07) . 1,10 = 0,1470 0,147* 0,20 0,10* 0,154 0,15* 0,123 0,25* 0,126 0,30 * 0,168 14,50% 15) Se está considerando invertir en la acción de la Cia Z, se espera que Z gane un retorno del 16%, su beta es de 1,4 , la tasa libre de riesgo es 8% y el rendimiento esperado del mercado es 14%. Se debería invertir en Z? Según el CAPM el retorno estimado de Z será: Rz 8 (14 8) *1,4 16,4% Ya que el retorno que se espera es menor que el valor que se espera en equilibrio, no debería invertir en Z. 16) Con referencia al problema anterior, qué se debería hacer si la beta de Z es 1,2? Los demás datos no cambian. Rz 8 (14 8) *1,2 15,2% Ya que el retorno esperado el mayor a la tasa de equilibrio, se debería invertir en Z. Nota: La tasa de retorno en equilibrio que provee la recta del mercado de valores, llamada SML, es la mínima tasa de retorno que un inversor debe aceptar de un título. Entonces para que la acción sean una buena compra, la tasa de retorno mínima requerida deberá ser calculada utilizando la recta SML. Por otro lado el rendimiento esperado considera a los activos individualmente, mientras que el rendimiento estimado según el modelo considera la variación de los activos respecto del retorno medio del mercado. 8

