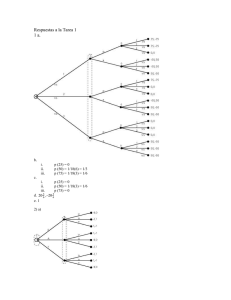
Tarea 1.

Primera tarea de Teoría de Juegos y Simulación:
Responde todas las preguntas señalando de forma resumida cada uno de los pasos que hayas
seguido, el razonamiento y los supuestos detrás de éstos.
1) El jugador 1 selecciona un número en un dado de seis lados, pero no se lo muestra al jugador 2. (Para
propósitos de este juego el 1 y 2 valen 1; el 3 y 4 valen 2; y el 5 y 6 valen 3) El jugador 2 debe decidir si
pasar, o arrojar un dado alterno, también de seis lados. Si el jugador 2 pasa, debe pagarle al jugador 1, $50
pesos. Si decide arrojar el dado y la suma de ambos dados es menor o igual a tres, el jugador 1 debe
pagarle al jugador 2 los $50 pesos, pero si la suma es mayor que tres, el jugador 2 pierde y debe pagarle al
jugador 1, $50 pesos. Si el jugador 2 pasa, el jugador 1 debe arrojar el dado alterno, y sumar el resultado al
número que eligió inicialmente. En caso de que la suma sea mayor que tres, pierde y debe pagarle al
jugador 2, 50 pesos, pero si la suma es menor o igual a tres el jugador 1 gana y cobra 25 pesos más.
A) Plantea el juego de forma extensiva
B) Cual es la probabilidad de que el jugador 1 gane:
i. 25 pesos
ii. 50 pesos
iii. 75 pesos
C) Cuál es la probabilidad de que el jugador 2 gane:
i. 25 pesos
ii. 50 pesos
iii. 75 pesos
D) ¿Cuál es el pago esperado del juego para cada jugador?
E) ¿Qué jugador preferirías ser? (suponiendo que eres racional) ¿Por qué?
2)
A) Plantea el juego de Piedra, papel y tijera en forma extensiva y estratégica.
B) ¿cuánto pueden esperar ganar ambos jugadores si:
i. Si cada uno asigna una probabilidad de 1/3 a cada opción
ii. Si el jugador A sólo juega piedra y el B juega las tres opciones
alternadamente.
iii. Si el jugador A sólo juega piedra y papel con probabilidades de 0.6 y 0.4,
respectivamente, y el jugador B sólo juega papel y tijera con probabilidades
de 0.3 y 0.7 respectivamente?
C) ¿De las tres opciones del inciso B, cual representaría la mejor estrategia para ambos
jugadores?
3) Encuentra los valores maximin y minimax y los puntos de silla correspondientes para los siguientes
juegos. ¿Son estables o inestables?
a.
A
B
C
D
A
5
9
10
8
B
4
6
1
4
C
-3
2
6
3
D
4
8
-6
1
E
4
8
1
1
b.
A
B
A
4, -4
4, -4
B
2, -2
2, -2
C
8, - 8
7, -7
D
6, -6
7, -7
c.
A
B
C
A
4
6
6
B
6
4
8
C
8
8
4
4) Identifica si hay o no estrategias dominadas y reduce las matrices de los siguientes juegos, pueden
encontrarse los puntos de equilibrio?
a.
A B C
A 10 12 11
B 12 13 15
C 11 11 11
b.
A
B
C
A
24
12
20
B
8
10
1
C
-2
4
2
5)
Cierto país en Sudamérica será el anfitrión a una conferencia sobre desarrollo económico y
cooperación regional a la que asistirán 10 países de la zona. Al país anfitrión le interesa la firma de un
tratado en el que un país limítrofe acordará bajar las tarifas arancelarias a la importación de azúcar, lo cual
representará un ingreso de 100 millones de dólares a la industria azucarera del país anfitrión en el próximo
año. A cambio, el país anfitrión reducirá las tarifas arancelarias para la importación de instrumentos
quirúrgicos desde ese país limítrofe que es una rama industrial que a dicho país le interesa desarrollar. Las
exportaciones de material quirúrgico representarán un ingreso adicional de 50 millones de dólares en el
próximo año. La actividad económica actual entre los dos países es como sigue: Las exportaciones del país
anfitrión hacia el otro son de 150 millones, pero el país anfitrión sólo importa productos con un valor de 30
millones de su vecino actualmente.
Sin embargo, existe un clima de desconcierto entre los dos países, pues desde hace décadas, el país
anfitrión ha extraído del manto acuífero común a la frontera entre ambos países más agua de la que le
corresponde, creando un déficit de este recurso al país vecino. El país afectado, está demandando 150
millones de dólares como pago del agua que el otro país ha extraído en exceso. Con este dinero se
construirá la infraestructura necesaria para explotar mantos de agua alternativos, pues el manto acuífero
común está en riesgo de secarse y asociaciones ecologistas internacionales han presionado a ambos
gobiernos para que no sea explotado más allá de ciertos límites. En caso de no recibir el pago, ello
representaría una pérdida de 80 millones de dólares a la economía local del país demandante en el próximo
año.
Por un lado, al país anfitrión le interesan los ingresos nuevos por exportación de azúcar y
conservar la actividad económica con el otro país, pero no quiere pagar la deuda de agua. A la otra nación,
le interesan las nuevas exportaciones de material quirúrgico, mantener la actual actividad económica y que
les sea pagada la deuda de agua.
El país anfitrión debe decidir si invitar a este país o no a la conferencia sobre desarrollo
económico y cooperación regional y adicionalmente, pasará al congreso local, en un término de seis meses
después de la conferencia, la decisión de pagar o no la deuda.
El país vecino debe pasar a su congreso local la decisión de hacer o no una declaración al respecto
de la deuda de agua que existe, independientemente de si es invitado o no a la conferencia.
En caso de que el país vecino sea invitado a la conferencia, y este decida hacer una declaración
ante el resto de los países invitados, el país anfitrión se vería obligado a pagar la deuda de agua dada la
presión internacional que se generaría antes de pasar la resolución a su congreso local. Si esto sucediese, se
prevé que la actual actividad económica se mantenga y que se firmen los tratados de azúcar y material
quirúrgico.
Existe también la posibilidad de que el país invitado no haga esta declaración pues el congreso de
la nación anfitriona está compuesto por dos fracciones, una de las cuales tiene el 55% de la votación y sus
miembros probablemente aceptarían pagar la deuda. Si eso último sucediese la actividad económica actual
se mantendría y los tratados de azúcar y material quirúrgico tomarían efecto y se pagaría la deuda de agua.
El país anfitrión ha sugerido a la nación vecina, que dadas las altas probabilidades de que el
congreso acepte pagar, que no haga declaración alguna sobre el tema del agua en la conferencia sobre
desarrollo. Sin embargo, la nación vecina sabe que el 45% del congreso del otro país está compuesto por
diputados que estarían en contra de pagar la deuda de agua; y, si eso último sucediese, el clima
internacional para demandar el pago o llevar a cabo cualquier otra medida no sería propicio, por lo cual la
actividad económica actual se mantendría y los tratados de azúcar y material quirúrgico se habrían ya
firmado y tomarían efecto.
En caso de que el país vecino no fuese invitado a la conferencia, se sabe que no se firmarían los
nuevos acuerdos arancelarios. Sin embargo, se corren riesgos adicionales. Al no ser invitados, la nación
vecina podría seguir haciendo una declaración, en cuyo caso las relaciones políticas y económicas se
romperían.
El congreso del país vecino, está compuesto por dos fracciones mayoritarias, una de las cuales,
tiene el 65% de los miembros del congreso y se cree que estaría en contra de realizar una declaración, sean
o no invitados a la conferencia. Por otro lado, se cree que el otro 35% estará a favor de si hacer una
declaración siendo o no invitados. Al hacer una declaración, y por lo tanto romper relaciones, se terminaría
toda la actividad económica entre ambas naciones, y por supuesto, no se pagará la deuda. De no hacer
ninguna declaración, y no ser invitados, este país tendría que esperar a saber la resolución del congreso del
país vecino para saber si recibirá el pago de la deuda o no ante las mismas condiciones que si hubiese sido
invitado. En este caso, nuevamente, el clima internacional para realizar una nueva declaración y romper
relaciones, ya no sería propicio, por lo cual, se mantendrían los actuales intercambios económicos, y no se
pagaría la deuda de agua.
A) Representa el juego de forma extensiva.
B) Calcula las probabilidades de que cualquiera de las soluciones suceda explicando los
supuestos que utilices.
C) Calcula el pago esperado del juego para ambos países
i. con base en tu respuesta al inciso “B”.
ii. Suponiendo que existen posibilidades iguales para cada bifurcación del
árbol que creaste en el inciso “A” .
D) Plantea el juego matricialmente
E) Si tu fueras asesor del gobierno del país anfitrión, ¿que estrategia de acción le recomendarías
tomar a tu gobierno, y que estrategia de acción dirías que tomaría el otro país? ¿Por qué?
F) ¿Se puede predecir cómo se solucionará el conflicto entre los dos países con base a los
supuestos de racionalidad e inteligencia y tomando sólo en cuenta la información dada en el
planteamiento del problema? ¿Por qué?
G) Critica el planteamiento del juego y la solución a la que hayas llegado en un espacio de no
más de dos cuartillas.