Curso 07/08 (Primer Parcial)

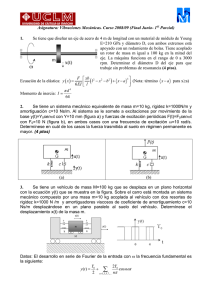
Asignatura: Vibraciones Mecánicas. Curso 2007/08 (1er Parcial)
1.
Se tiene el sistema mecánico de la figura, compuesto por una varilla AC rígida de
longitud L, masa m y horizontal en la posición de equilibrio estática. Está articulada en el
extremo izquierdo al suelo y en el extremo derecho se acopla una masa puntual M. En los
puntos B y C (AB=L/3 y AC=L) se acopla un
amortiguador
de
coeficiente
de
amortiguamiento c y dos resortes de rigidez
k, tal y como se muestra en la figura. El
techo se puede mover subiendo o bajando
en función del tiempo y(t) excitando el
sistema mecánico. Determínese la ecuación
que gobierna el movimiento del sistema y
parámetros del sistema equivalente para el
estudio del giro de la varilla θ(t). (4 ptos):
2.
Se tiene un sistema mecánico equivalente de masa m=100 kg, rigidez k=10000
N/m y amortiguación c=3000 Ns/m. El sistema inicialmente
está en la posición x0=10 cm con velocidad nula, en ese
mismo instante se somete a una excitación por movimiento
de la base y(t)=Ysen(ωt) con Y=5 mm y ω=10 rad/s.
Determínese la respuesta del sistema. (4 ptos)
3.
Se tiene una viga de masa despreciable en voladizo como soporte de un motor, un
extremo está empotrado en la pared y en el otro se monta el motor eléctrico de masa 100
kg, girando a una velocidad nominal de 1000 rpm con un
desequilibrio de 10 kg⋅mm. Cunado se instaló encima de la
viga el motor se produjo un desplazamiento estático de 1 cm.
En los ensayos de caracterización se determinó un
amortiguamiento viscoso equivalente ce=500 Ns/m.
Determínese la fuerza transmitida a la pared (estática y
dinámica) con el motor girando a su velocidad nominal. (4
ptos):
4.
El sistema de la figura está formado por una varilla en posición vertical empotrada
al suelo y un motor fijado en su extremo. La varilla tiene diámetro D= 2cm, longitud L=20
cm, densidad ρ=7800 kg/m3, módulo elástico E=210 GPa y un amortiguamiento viscoso
tanto en dirección vertical como horizontal de coeficiente ξ=0.1. En cuanto al motor, su
masa es M=2 kg, su rango de funcionamiento es de [0-5000] rpm y presenta un
desequilibrio definido por una distancia d=5mm y una masa desequilibrada md=250 g
(incluida en M). Con todos estos datos se pide determinar:
a) Sistema equivalente lineal de un grado de libertad para la vibración
del sistema en dirección horizontal (x) y sistema equivalente lineal de
un grado de libertad para la vibración en dirección vertical (y). Indicar
además los valores de ωd para cada uno de los casos. (2 puntos)
b) Sin que el motor esté en funcionamiento, calcular el máximo
desplazamiento en dirección horizontal (x) cuando el sistema se pone
a vibrar desde su posición de equilibrio con una velocidad de
X = 10mm / s . (3 puntos)
c) Con el sistema inicialmente en reposo, el motor se pone en
funcionamiento hasta que alcanza una velocidad de giro de 20000
rpm. Calcular el máximo desplazamiento en régimen permanente
tanto en dirección horizontal (x) como vertical (y) y justificar que
dirección de vibración es más desfavorable en el rango de
funcionamiento del motor. (3 puntos)
Datos:
meq, axil = M +
mviga
3
meq, flexión = M + 0.23mviga
x( y ) =
I=
π
4
Fy 2
(3L − y )
6 EI
R4